행렬의 수많은 특징은 거듭 강조하듯이 행렬의 '랭크(rank)'가 보유하고 있습니다.
그 다음으로 행렬의 특징을 관찰하는데 좋은 도구는 행렬의 영공간, 행공간, 열공간을 들여다 보는 것입니다. 어쩌면 이들이 모여 랭크라는 우아한 숫자를 건설한 것으로도 볼 수 있는데, 이들은 공간이라는 단어가 들어가 있듯이 행렬에 벡터공간의 논리를 적용한 것입니다. 이것이 가능한 까닭은 행렬은 행들과 열들로 쪼개어 바라볼 수 있고, 각각의 행과 열은 행벡터와 열벡터라는 '벡터'로 생각할 수 있기 때문입니다. 그러면 자연스레 행렬에 대한 벡터공간을 논의할 수 있게 됩니다.

행렬 자체는 벡터공간이라 할 수 있어 행과 열을 따로 보아 행벡터와 열벡터가 만드는 벡터공간이 연립방정식에서 매우 중요한 역할을 합니다. 특히 열벡터의 선형결합으로 만들어지는 벡터공간인 열공간은 연립방정식 Ax=b 의 해를 찾는 핵심적인 열쇠입니다.
1. 행렬은 벡터공간이다.
성분이 체(field)인 m×n 행렬은 Mm,n(F) 로 표기하고, 이것은 벡터공간입니다. 이것을 엄밀히 증명하려면 벡터공간의 8공리를 만족해야 하는데, 간단하게 행렬끼리의 합과 스칼라 곱을
(A+B)ij=Aij+Bij,(cA)ij=cAij
으로 정의하면 성립함을 직관적으로 이해할 수 있을 것입니다. 행렬의 덧셈과 상수배(스칼라 곱)은 행렬의 각 성분(=F의 원소)들끼리 더하고 상수배를 해주는 것이기 때문이죠.
2. 행공간과 열공간
[행공간과 열공간의 정의]
A∈Mm,n(F)인 행렬 A=(a11a12⋯a1na21a22⋯a21⋮⋮⋮am1am2⋯amn)
에 대하여, A의 m개 행들 r1=(a11a12⋯a1n)r2=(a21a22⋯a2n)⋮rm=(am1am2⋯amn)
의 선형결합으로 생성(span)된 부분공간 R(A)={r1,r2,⋯,rm} 를 행렬 A의 '행공간(Row space)'이라 부르며, A의 n개의 열들
c1=(a11a21⋮am1),c2=(a12a22⋮am2),⋯,cn=(a1na2n⋮amn)
의 선형결합으로 생성(span)된 부분공간 C(A)={c1,c2,⋯,cn}을 행렬 A의 '열공간(Column space)'이라 부른다.
3. 행공간과 열공간의 차원은 행렬의 랭크와 같다.
어떤 행렬의 특성을 가장 잘 나타내는 지표는 단언코 행렬의 랭크입니다. 행렬의 랭크는 행공간과 열공간의 랭크와 매우 밀접한 관련(셋은 같음)을 맺고 있고 그에 관한 정리를 소개할 것입니다. 우선, 행렬의 랭크를 구하기 위해서는 그 행렬에서 선형독립인 최대의 행의 개수를 세거나, 열의 개수를 세면 된다고 했었습니다. 이 때 행의 개수와 열의 개수가 달라도, 행렬의 랭크를 구할 때 선형독립인 최대 행의 개수를 구하든 열의 개수를 구하든 랭크는 똑같은 값을 가짐을 위 포스팅에서 설명했었지요. 행공간과 열공간의 차원은 각각 그들의 랭크와 같으며 동시에 행렬의 랭크(rank)와 같습니다. 이는 어떻게 보면 유도된다기보다, 행공간과 열공간의 차원(랭크)는 항상 같고 그것을 그냥 간단히 행렬의 랭크(rank)로 정의한 셈입니다.
정리(L.A) 2.3
임의의 A∈Mm,n(F)에 대하여 행렬 A의 랭크(rank)는 A의 행랭크(=열랭크)로 정의되고, 다음이 항상 성립한다.
rank(A)=dim(R(A))=dim(C(A))=rank(AT)
행랭크와 열랭크가 같다는 사실을 보이면 전치행렬의 랭크는 원래 행렬의 랭크와 똑같음을 보일 수 있기 때문에 전치행렬의 랭크에 관한 식이 하나 추가된 것입니다. 이는 여태껏 설명에 의해 직관적으로 납득되지만, 정확한 수학적 증명은 다음에 해보도록 하겠습니다.
4. 연립방정식 Ax=b는 열공간(Coulumn space)이 중요하다.
다다음 포스팅에선 영공간과 동차 연립방정식 Ax=0 을 해결하는 방법을 소개할 것입니다. 반면에,
비동차 연립방정식 Ax=b을 푸는 것은 열공간과 연결되어 있습니다. Ax=b 에 대하여 행렬 A와 미지수 벡터(이것도 행렬이긴 함) x의 곱셈을 바라보는 두 가지 관점을 일전에 제시한 바 있습니다. 그 중 하나는 A의 열벡터들이 x의 각 성분을 앞에 스칼라로 달아 선형결합한 꼴로 해석하는 것이었습니다. 가령 A가 3×3 행렬이라면,
Ax=x(FirstcolumnofA)+y(SecondcolumnofA)+z(ThirdcolumnofA)=b
입니다. 예시를 하나 들어 이것을 구체적으로 파악해 봅시다. 연립방정식이 다음과 같이 주어져 있습니다.
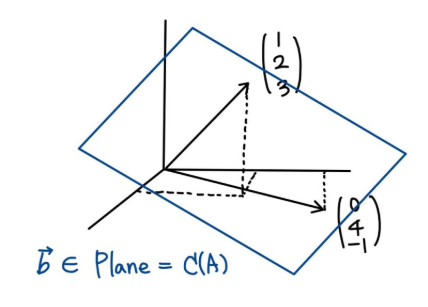
Ax=(10243−1)(xy)=b
이것을 만족하는 해는 b인데, 어떤 값들이 b가 될 수 있을까요? 행렬 곱의 선형결합적 관점에서 바라보면, b는 행렬 A의 열벡터들이 만들어내는 벡터공간의 원소가 되어야 합니다. 즉, b는 A의 열공간에 포함되어 있어야 한다는 것입니다. 곧, b=x(123)+y(04−1)⇔Ax=b
정리(L.A) 2.4
연립방정식 Ax=b 에서 b가 A의 열공간 C(A)에 포함되어 있을 때만 해를 구할 수 있다. (필요충분조건)
여기서 열공간은 A의 열들이 만드는 벡터공간인데, A의 열의 개수는 2개이고 각각 성분이 3개입니다. 그렇다면 3차원 벡터 2개(두 벡터는 서로 독립)의 선형결합으로 만들어지는 A의 열공간은 3차원 공간에 존재하는 2차원 평면입니다. 그리하여 간략히 그림을 그리면 다음과 같이 나타낼 수 있습니다. 평면의 기저로 A의 두 열벡터가 선택된 것입니다. 이 평면 속의 임의의 점을 가리키는 벡터가 방정식 Ax=b 의 b 자리에 와야 해가 존재한다고 할 수 있게 됩니다.
'선형대수학(Linear Algebra) > 행렬과 행렬식' 카테고리의 다른 글
| 행렬의 영공간 (The Nullspace of Matrix) (0) | 2020.11.30 |
|---|---|
| 연립방정식의 해공간과 관련된 중요한 정리(The significant Theorem related with solution space of system of equation) (2) | 2020.11.30 |
| 행렬의 계수, 랭크(The Rank of matrix) (7) | 2020.11.29 |
| 선형 연립일차방정식 3) 소거행렬과 치환행렬(Elimination matrix and Permutation matrix) (2) | 2020.11.29 |
| 선형 연립일차방정식 2) 피벗과 소거법(Pivots and Elimination method) (0) | 2020.11.29 |


댓글