점성, 열전도율, 확산(Viscosity, Thermal conductivity, Diffusion)

기체의 운동 특성은 다음 세 가지 요인을 고려하는 것이다.

 

점성(viscosity) : 이것은 운동량($\mathbf{p}$)의 이동(전달)이다.
열전도율(thermal conductivity) : 이것은 열($Q$)의 이동(전달)이다.
확산(diffusion) : 이것은 입자들($N$)의 이동(전달)이다.

---

1. 점성(Viscosity)

 

흔히 점성이 높을수록 유체는 잘 흐르지 못한다고 말한다. 다시 말해 점성은 유동성(fluidity)와 반비례하는 관계에 놓여 있다. 액체에 대해서 잠시 예를 들자면, 마그마(magma)는 그것의 주 구성 성분인 이산화규소(SiO2)의 성분이 많을수록 점성이 높은 특징을 가지기 때문에 SiO2 비율이 낮은 현무암질 마그마는 유동성이 높아 멀리까지 퍼지고 점성이 낮고, 상대적으로 유문암질 마그마는 유동성이 낮아 멀리까지 흐르지 못하며 점성이 높은 편이다. 하와이는 열점(Hot spot)에서 만들어진 현무암질 화산체로 하와이의 용암 분출을 보면 폭발적이지는 않지만, 매우 먼 지점까지 흘러 거주지까지 위협을 가하는 상황을 종종 목격할 수 있다.

 

하지만 우리는 지금 기체의 점성에 대해서 다루고 있다.^[각주:1] 그렇다면 점성이란 무엇인가? 점성은 층밀리기 변형력(Shear stress)에 의해 발생하는 변형에 대한 유체의 저항성을 측정한 것이다. 점성의 크기를 측정하기 위해 다음의 그림을 참조하자.

 

 

그림과 같이 유체가 면적 A인 두 개의 판 사이에 끼어 있는 상황을 고려한다. 방향 표시를 보면 이 판은 $xy$ 평면에 놓여 있는데, 아래쪽 판은 정지해 있고 위쪽 판은 속력 $u$로 미끄러지는 상황을 고려한다. 그러면 여기서 층밀리기 변형력은

 

$$\tau_{xz} = \frac{F}{A}$$

 

이 유체에 작용하게 된다. $\tau_{xz}$ 의 뜻은 $z$에 수직한 면, 즉 $z$방향 법선벡터를 갖는 평면이 $x$방향으로 받는 힘을 가리키고 일반적으로 텐서다. 직관적으로 층밀리기 변형력은 층들에 수직한 방향의 속도 기울기에 비례함을 알 수 있다. 속도 기울기는 가속도를 의미한다 볼 수 있고 결국 힘이 클수록 층밀리기 변형력이 크다는 뜻이다. 비례관계를 등식으로 바꾸려면 상수가 필요하고 이 비례상수는 $\eta$ 로 표기하며, '점성계수(coefficient of viscosity)'라 부르며 이것이 곧 '점성(Viscosity)'이다.

 

$$\tau_{xz} = \frac{F}{A}= \eta\,\frac{\partial \left\langle u_x \right\rangle}{\partial z}$$

 

층밀리기 힘 $F$가 위 판의 우측으로 작용하면, 속도는 아래쪽으로 갈수록 작아지기 때문에 속도 기울기가 증가하는 방향은 $+z$ 방향이 된다. 이 때 속도 기울기를 쓸 때 평균값을 취하는데, 위 판에서는 $\left\langle u_x \right\rangle=u$ 이고 아래 판에서는 $\left\langle u_x \right\rangle=0$ 으로 생각하면 된다. 그럼 $\left\langle u_x \right\rangle$는 평균값을 뜻한다. 

 

위 판에 가해진 힘은 $+x$ 방향으로 알짜 운동량을 전달하게 된다. 그렇기 때문에 운동량 선속(momentum flux)의 방향은 속도 기울기와 반대 방향이 된다. 속도는 위에서 아래로 갈수록 줄어들기 때문이다. 따라서 음의 부호를 달아

 

$$\Pi_z=-\eta\,\frac{\partial \left\langle u_x \right\rangle}{\partial z}$$

 

와 같이 운동량 선속을 정의할 수 있다. 그런데 기체 운동론에 의하면 단위 시간동안 단위 면적을 때리는 분자의 수는

 

$$v\cos \theta \,nf(v)\frac{1}{2}\sin \theta d\theta$$ 

 

로 주어지기 때문에, $z$ 방향으로 이동하는 분자들은 마지막 충돌 이후 평균 자유 거리 $\lambda$ 만큼 이동하게 되니, $z$ 방향으로는 $\lambda \cos \theta$ 만큼 이동하게 된다. 이 거리를 이동하는 동안 $\displaystyle \frac{\partial \left\langle u_x \right\rangle}{\partial z}\lambda \cos \theta$ 만큼의 속도 평균 증가가 존재하여, 위로 움직이고 있는 기체 입자는 $+x$ 방향의 운동량이 결손된다. 곧 주변에 $x$방향으로의 여분의 운동량을 주고, 자신들은 그 양을 잃게 되므로 음의 부호를 달면 운동량의 결손량은

 

$$-m\frac{\partial \left\langle u_x \right\rangle}{\partial z}\lambda\cos \theta$$

 

전달하는 총 $x$ 방향 운동량은 운동량 선속이고, 적분을 통해 구한다.

 

$$\begin{align*}
\Pi_z&=\int_{0}^{\infty}dv\int_{0}^{\pi}d\theta \;v\cos\theta \,nf(v)\frac{1}{2}\sin \theta\, \cdot 
\left\{ -m\frac{\partial \left\langle u_x \right\rangle}{\partial z}\lambda\cos \theta \right\}
\\\\&=-\frac{1}{3}nm\lambda \left\langle v \right\rangle\left( \frac{\partial \left\langle u_x \right\rangle}{\partial z} \right)
\end{align*}$$

 

계수를 뽑으면 점성을 얻는다.

 

기체의 점성 or 점성계수는 다음과 같이 주어진다.
$$\eta = \frac{1}{3}nm\lambda \left\langle v \right\rangle$$

 

$$\lambda\simeq \frac{1}{\sqrt{2}n\sigma}$$

 

임을 고려하면, $\eta$는 $n$에 무관하고 $\sqrt{T}$ 에 비례하므로 기체의 점성은 온도와 함께 증가한다. 서두에서도 언급했듯이, 이는 액체와는 다른 현상임을 기억하자.

---

2. 열전도율(Thermal conductivity)

 

열은 고온에서 저온으로 이동하는 열에너지로 정의된다. 열이 저온에서 고온으로 흐를 수는 없고, 그렇기 때문에 열의 이동 방향은 단방향이다.^[각주:2] 그런데 온도가 얼마나 빨리 바뀌는지, 즉 이동하는 열의 양은 물질의 열전도율에 의존한다.

 

열의 흐름은 열 선속 벡터(heat flux vector)에 의해 기술되고 기호로는 $\mathbf{J}$ 이다. 이 벡터의 방향은 열 흐름의 방향과 같고, 온도 기울기의 반대 방향으로 정의한다. 그 뜻은 온도 기울기의 방향을 저온에서 고온으로 정하겠다는 뜻이다.

 

$$J_z=-\kappa \left( \frac{\partial T}{\partial z} \right)$$

 

여기서 비례상수 $\kappa$ 가 바로 '열전도율(thermal conductivity)'에 해당하는 물리량이다. 온도 기울기는 3차원에서 그래디언트를 사용해 

 

$$\mathbf{J}=-\kappa \nabla T$$

 

로 적을 수 있다.

 

그런데 기체 분자들은 열을 어떻게 운반하는 것일까? 기체 분자들의 열 운반은 그들의 평균 병진 운동에너지가 증가하여 온도가 증가하기 때문이라고 생각할 수 있다. 그러면 기체의 온도를 증가시켜야 열이 이동된다는 것이고 기체 온도를 증가시켜 분자 하나당 평균 운동에너지를 올려 주어야 한다는 것인데, 이와 관련된 물리량은 바로 열용량 $C$이다. 기체 분자 한 개의의 열용량을 $C_{\mathrm{molecule}}$ 이라 적으면 온도를 1K 상승시키기 위해선 이 값이 $\displaystyle\frac{3}{2}k_B$ 와 같음을 이미 알고 있다.

 

열전도율을 구하기 위해 점성에서 했던 것과 동일한 논의를 한다. $z$축을 따라 움직이는 분자들은 마지막 충돌 이후 평균 자유 거리 $\lambda$ 만큼을 이동하고, $z$축 방향으로는 $\lambda\cos\theta$ 만큼을 이동하게 된다. 그들이 잃은 열에너지를 계산하면 

 

$$Q=-C_{\mathrm{molecule}}\times \Delta T=-C_{\mathrm{molecule}}\left( \frac{\partial T}{\partial z} \right)
\lambda\cos\theta$$

 

적분을 통해 단위 시간동안 단위 면적을 가로질러 이동하는 총 열에너지를 구한다. 이는 열 선속(heat flux)가 되며

 

$$\begin{align*}
J_z=&\int_{0}^{\infty}dv\int_{0}^{\pi}d\theta \;C_{\mathrm{molecule}}\left( \frac{\partial T}{\partial z} \right)
\lambda\cos\theta v\cos\theta \;nf(v)\frac{1}{2}\sin\theta\\\\=& -\frac{1}{3}nC_{\mathrm{molecule}}
\lambda\left\langle v \right\rangle\frac{\partial T}{\partial z}
\end{align*}$$

 

마침내 열전도율 값을 얻는다.

 

기체의 열전도율은 다음과 같이 주어진다.
$$\kappa = \frac{1}{3}C_V\lambda \left\langle v \right\rangle$$ 여기서 $C_V=nC_{\mathrm{molecule}}$ 으로, 단위 부피당 분자의 개수에 분자 1개의 열용량을 곱해준 값이다.

 

$$\lambda\simeq \frac{1}{\sqrt{2}n\sigma}$$

 

임을 고려하면, 이번에도 $\kappa$ 가 $\sqrt{T}$ 에 비례함을 알 수 있으니, 열전도율은 온도가 높을수록 증가하는 특징을 가진다.

---

3. 확산(Diffusion)

 

마지막으로 논의할 것은 확산이다. 확산은 뒤의 열확산 방정식에서 중요한 역할을 한다.

 

 

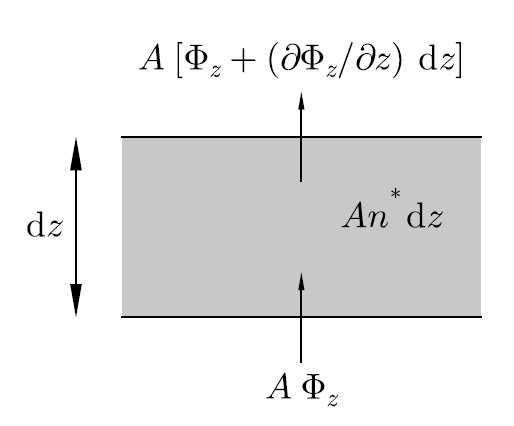
확산을 논의하기 위해 그림과 같이 두께가 $dz$이고 단면적이 $A$인 영역에 보통의 분자들과 우리가 주목해서 볼 특별히 표시가 된 분자들이 섞여 있다고 가정하자. 표시가 된 분자들은 단위 부피당 $n^*(z)$개가 있다고 가정한다. 즉 $n^*$를 $z)$에 대한 함수로 볼 수 있다는 뜻이다. 왜냐하면 이 표시된 분자들의 $z$방향에 평행한 선속을 측정할 것이고 이 선속을

 

$$\Phi_z=-D\left( \frac{\partial n^*}{\partial z} \right)$$

 

와 같이 정의하자. 이 때 앞에 붙은 상수 $D$가 '자체 확산 계수(Coefficient of self-diffusion)'이라 불리는 물리량이다. 이 식은 열전도율을 논의했을 때와 같이, 3차원일 때는

 

$$\Phi_z=-D\nabla n^*$$

 

로 표현할 수 있다. 이 식은 '픽의 법칙(Fick's law)'라 부른다.

 

그림의 영역에서 판 안으로 들어가는 선속은 

 

$$A\Phi_z$$

 

이고, 나가는 선속과 들어오는 선속의 차이가 $d\Phi_z$ 라면, 이 판에서 나가는 선속은

 

$$A\left( \Phi_z+\frac{\partial \Phi_z}{\partial x}dz \right)$$

 

이 되어야 마땅하다. 입자는 갑자기 사라지거나 생성되지 않으므로, 선속의 차이만큼이 영역 안에서 시간에 따라 변화하는 입자의 수라 볼 수 있다. 이를 바탕으로 등식을 세워보자.

 

$$-A\frac{\partial \Phi_z}{\partial x}dz =\frac{\partial }{\partial t}\left( An^*dz \right)$$

 

참고로 여기서 $An^* dz$ 는 이 부피값에 $n^*$을 곱해준 것이다. 그러니 부피 안의 표시되어 있는 분자들의 총 개수를 말하는 것이다. 위 식을 정리하면

 

$$-\frac{\partial \Phi_z}{\partial x}dz =\frac{\partial n }{\partial t}$$

 

선속 식을 대입하여 정리하면 다음을 얻는다.

 

확산 방정식(diffusion equation)은
$$\frac{\partial n^*}{\partial t}=D\frac{\partial ^2n^*}{\partial z^2}$$ 이다. 3차원에서의 일반적인 확산 방정식은 선속에 픽의 법칙을 대입해서 얻고,
$$\frac{\partial n^*}{\partial t}=D\nabla^2 n^*$$ 와 같이 나타낸다.

 

마지막으로, 1과 2에서 했던 것처럼 자체 확산 계수를 적분을 통해 구해보자. 단위 시간동안 단위 면적을 때리는 표시가 된 특정 분자들에 대하여

 

$$\begin{align*}
\Phi_z&=\int_{0}^{\infty}dv\int_{0}^{\pi}d\theta \;v\cos\theta \,nf(v)\frac{1}{2}\sin \theta\, \cdot 
\left\{ -\frac{\partial \left\langle n^* \right\rangle}{\partial z}\lambda\cos \theta \right\}
\\\\&=-\frac{1}{3}\lambda \left\langle v \right\rangle\left( \frac{\partial n^*}{\partial z} \right)
\end{align*} \\\\$$

 

자체 확산 계수(Coefficient of self-diffusion)은 다음과 같이 주어진다.
$$D=\displaystyle\frac{1}{3}\lambda\left\langle v \right\rangle$$

 

$$\lambda\simeq \frac{1}{\sqrt{2}n\sigma} $$

 

을 고려하자. 이상 기체 상태 방정식 $pV=nRT$ 를 고려한다면 $D$는 $\displaystyle\frac{1}{p}$ 에 비례하므로, 압력이 증가함에 따라 확산은 저지되는 경향성을 갖는다.

 

또한 마찬가지로 이상 기체 상태 방정식을 생각하면 $D$의 값은 $T^{\frac{3}{2}}$ 에 비례하기에, 고정된 압력에서 확산은 온도가 높을수록 잘 발생한다. 열전도율과 점성은 $\sqrt{T}$ 에 비례했던 것과 차이를 기억하자.

 

 

 

1. 기체와 액체의 점성에 관한 성질은 약간의 차이점이 있다. 실제로 기체에서는 온도와 점성이 비례하지만, 액체에서는 온도와 점성이 반비례 관계에 놓여 있다. 즉 온도와 유동성이 비례한다. [본문으로]
2. 이는 추후 열역학 법칙을 논할 때 구체화한다. [본문으로]