집합 $A$의 원소의 개수를 중고교 수학에서 $n(A)$ 라 표기합니다. 그리고 원소의 개수는 유한집합에 대해 셀 수 있다고 말합니다. 무언가의 개수를 셀 수 있다는 말을 하기 위해서는, 일단 개수에는 한계가 존재해야 하고, 정확히 몇 개인지 자연수를 통해서 나타내야 합니다. 예를 들어서 개수를 셀 때 3.5개1나 $\sqrt{2}$ 개라는 표현은 좀처럼 사용하지 않습니다.
그러면 무한집합에 대해서는 어떠할까요? 무한집합의 원소의 개수는 셀 수 없는 것처럼 보입니다. 끝이 없기 때문이죠. 하지만 이러한 직관이 수학적으로 꼭 옳지 않을 수 있다는 사실에 대해 분석해 보려고 합니다. 예를 들어, 수직선에서 $[0,100]$을 생각해봅시다. 자연수의 개수와 정수의 개수는 분명이 셀 수 있고 유한합니다. 하지만 유리수의 숫자는 어떠할까요? 무리수의 숫자는 어떠할까요? 유리수와 무리수의 개수는 무한히 많아 보입니다. 그렇다면 어떤 수가 더 많을까요? 확률적인 관점에서 마치 이런 것입니다. $[0,100]$에 임의로 다트를 하나 던져 맞춘다고 하였을 때 그 수가 유리수일 확률과 무리수일 확률 중 무엇이 더 높을까요? 이러한 문제들에 대한 답을 구하기 위해 앞으로 셀 수 있다는 개념, 무한과 유한의 개념을 수학에서 어떻게 정의하는지 보고, 우리가 알고 있는 수 집합에 대해 원소의 개수를 셈해 보려고 합니다.
1. 유한집합과 무한집합
일단, 앞으로 집합의 농도(cardinality)를 정의하기 전까지는, 집합 $A$ 의 원소를 나타내는 기호로 $\left| A \right|$ 를 쓰겠습니다. 이는 절댓값 기호와 모양은 똑같은데, 원래 집합의 농도를 나타내는 의미이고, 농도는 지금 단계에서 단순히 집합의 원소 갯수라고 생각하면 됩니다. 추후에 자세한 개념을 학습하면 정의를 다시 할 예정입니다. 그래서 편의상 제가 자의적으로, 그 전까지 $\left| A \right|=\infty$ 라는 표기를 쓸 것인데 이것은 원소의 개수가 무한한, 즉 $A$ 가 무한집합이라는 뜻으로 사용할 것입니다.2
정의($S.T$) 4-1) 유한집합과 무한집합
공집합이 아닌 집합 $X$ 에 대하여 $Y\subset X$(진부분집합)인 $Y$ 가 존재하여, $X$와 $Y$ 사이에 일대일 대응인 함수 $f:X\rightarrow Y$ 가 존재할 때3, $X$ 를 '무한집합(infinite set)'이라 한다. 무한집합이 아닌 집합은 '유한집합(finite set)'이라 한다.
이게 무슨 말일까요? $X$와 $X$ 의 진부분집합 $Y$ 로의 일대일대응을 만들 수 있어야 한다는 것입니다. 그런데 일대일대응이라는 것은 일대일함수(one-to-one) 즉 단사(injective)이고 동시에 전사(surjective), 즉 위로(onto)의 함수여야 한다는 것인데 직관적으로, 또는 우리가 지금까지 알고 있는 개념에 의하면 어떻게 $X$에서 그것의 진부분집합 $Y$ 로의 일대일대응이 가능하다는 것인지 이해하기 어려울 수 있습니다. 그러니 다음 예시를 살펴보겠습니다.
예제 1) 자연수 집합 $\mathbb{N}$ 은 무한집합인가? 위의 정의를 통해 분석해보아라.
자연수 집합 $\mathbb{N}$ 은 분명히 위 정의를 생각하지 않고서도 무한집합이라는 것을 알고 계실 것입니다. 무한집합의 특징을 생각해서, 위의 정의에서 말하는 일대일대응을 생각해 봅시다.
Sol) $f:\mathbb{N}\rightarrow \mathbb{N}-\left\{ 1 \right\}$ 를 $n\longmapsto n+1$ 이라 정의하자. 그러면 $f$는 일대일함수이고, 공역이 정의역의 진부분집합이다. 따라서 정의($S.T$) 4-1) 에서 말하는 일대일대응인 함수 $f$ 를 만들 수 있으므로 $\mathbb{N}$ 은 무한집합이다.
처음엔 직관적으로 납득하기 어려울 수 있습니다. $n\longmapsto n+1$ 으로 함수를 만들면 언제나 하나가 남을 것 같다는 찝찝함이 존재하지요. 하지만 이는 무한에 대한 개념이 우리의 일상의 직관과 충돌하는 것으로, 자연수 집합의 상한이 없기 때문에, 무한히 $n\longmapsto n+1$ 의 방식으로 모든 원소를 일대일대응시킬 수 있습니다. 따라서, 위 정의에서 말하는 일대일대응이란 말그대로 하나씩 하나씩 대응할 수 있다는 개념에 가깝지 공역의 원소 개수를 셀 수 있고, 치역의 원소 개수를 셀 수 있을 때 그 셀 수 있는 두 (자연)수가 같다는 개념과는 차이가 있습니다.
예제 2) 공집합은 유한집합이다.
Sol) 공집합은 그것의 진부분집합이 존재할 수 없고, 따라서 일대일대응도 만들 수 없다. 즉 무한집합이 아니므로 유한집합이다.
예제 3) 단원소집합(singleton set)은 유한집합이다.
Sol) 단원소집합의 유일한 진부분집합은 공집합이고, 단원소집합과 공집합 사이에선 일대일대응을 만들 수 없어서, 무한집합이 아니므로 유한집합이다.
정리($S.T$) 4.1)
① 모든 무한집합의 초집합(superset)은 무한집합이다. 즉,
$$X\subseteq Y\;\wedge \;\left| X \right|=\infty \;\; \Rightarrow \;\;\; \left| Y \right|=\infty$$ ② 모든 유한집합의 부분집합은 유한집합이다. 즉,
$$X\subseteq Y \; \wedge \; \left| Y \right| < \infty \;\; \Rightarrow \;\; \left| X \right| < \infty$$
일단 $A\subseteq B$ 에서 $A$ 는 $B$ 의 부분집합이라 하고 $B$ 는 $A$ 의 초집합(superset)이라 하는 정의부터 기억한 뒤, 직관적으로 이해부터 해봅시다. 첫번째 문장은, 작은집합이 무한집합이면 그보다 크거나 같은 집합도 무한집합이어야만 한다는 것이고 두번째 내용은 큰 집합이 유한집합이면 그보다 같거나 작은 집합도 유한집합이어야만 한다는 것을 의미합니다. 둘은 우리의 직관에 전혀 어긋나지 않습니다.

증명) ①$X\subseteq Y$ 라 하고 $X$ 를 무한집합이라 하자. $X$ 가 무한집합이므로, $f(X)\neq X$ 즉 다시 말해$f(X)\subset X$ 인 단사함수 $f:X\rightarrow X$ 가 존재한다.4 $Y$ 가 무한집합임을 보이기 위해, 함수 $g:Y\rightarrow Y$ 를
$$g(y) = \left\{ \begin{array}{cl}
f(y) \;& \ y\in X \\
y \;& \ y\in Y-X
\end{array} \right.$$
와 같이 정의하자. 이때 $g$ 가 단사이고, $g(Y)\subset Y$ 즉 $g(Y)\neq Y$ 임을 보이면 된다.
1) $g$ 가 단사임을 먼저 보이자. 그러러면 $g(y_1)=g(y_2) \Rightarrow y_1=y_2$ 임을 확인해야 한다.
i) $g(y_1)=g(y_2) \in X$ 일 때 : $f(y_1)=g(y_1)=g(y_2)=f(y_2)$ 이고 $f$ 가 단사이므로 $y_1=y_2$ 이다.
ii) $g(y_1)\neq g(y_2) \in Y-X$ 일 때 : $g(y_1)=y_1$ 이고 $g(y_2)=y_2$ 이므로 $g(y_1)=g(y_2)$ 이면 $y_1=y_2$ 이다.
2) $g(Y)\neq Y$ 임을 보이자. $f(X)\subset X$ 이므로, $k\notin f(X)$ 인 $k\in X$ 가 존재한다. 그러면 $g(k)=f(k)\in f(X)$ 이므로 $k \notin g(Y)$ 이다. 고로 $g(Y)\neq Y$ 가 성립하여 $Y$ 는 무한집합이다.
② 귀류법을 사용하기 위해 $X \subseteq Y$ 이고 $Y$ 가 유한집합일 때 $X$ 가 무한집합이라고 가정하자. 그러면 위의 ①에 의하여 무한집합 $X$ 의 초집합 $Y$ 가 무한집합이어야 하고, 이는 모순이므로 주어진 명제는 참이다. $_\blacksquare$
정리($S.T$) 4.2)
일대일대응인 함수 $g:X\rightarrow Y$ 에 대하여, 정의역 $X$ 가 무한집합이면 공역 $Y$ 도 무한집합이다.
증명) $X$가 무한집합이므로, $f(X)\neq X$ 인 단사함수 $f:X\rightarrow X$ 가 존재한다. 또한 $g$ 가 일대일대응이면 $g^{-1}:Y\rightarrow X$ 또한 일대일대응이므로, $g^{-1}$ 에 의해 $Y\rightarrow X$ 로, 그리고 $f$ 를 통해 $X\rightarrow X$ 로, 마지막으로 $g$ 를 통해 $X\rightarrow Y$ 로 변환되는 합성함수
$$h=g\circ f\circ g^{-1}$$ 을 생각하면, 단수함수들($f,g,g^{-1}$)의 합성은 단사함수이므로 $h:Y\rightarrow Y$ 역시 단사함수이다.
또한,
$$\begin{align*}
h(Y)&=\left( g\circ f\circ g^{-1} \right)\left( Y \right)=\left( g\circ f \right)(g^{-1}(Y))
\\\\&=\left( g\circ f \right)(X)=g(f(X))
\end{align*}$$ 이고, $X$ 가 무한집합이므로 $f(X)\subset X$ 이고 $g$ 가 일대일함수이므로 $g(f(X)) \subset Y$ 가 된다. 즉, $g(f(X)) \neq Y$ 이므로 $h(Y)\subset Y$ 이다. 따라서 $h(Y)\subset Y$ 인 단사함수 $h:Y\rightarrow Y$ 가 존재하므로 $Y$ 는 무한집합이다. $_\blacksquare$

따름정리($S.T$) 4.2.1)
일대일대응인 함수 $g:X\rightarrow Y$ 에 대하여, 정의역 $X$ 가 유한집합이면 공역 $Y$ 도 유한집합이다
증명) 귀류법을 사용하여 공역 $Y$ 가 무한집합이라고 가정하자. 그러면 일대일대응인 함수 $g^{-1}:Y\rightarrow X$ 에서 정의역이 무한집합이므로 위의 정리($S.T$) 4.2) 에 의하여 공역 $X$ 는 무한집합이고, 이는 가정에 모순이므로 주어진 명제는 참이다. $_\blacksquare$
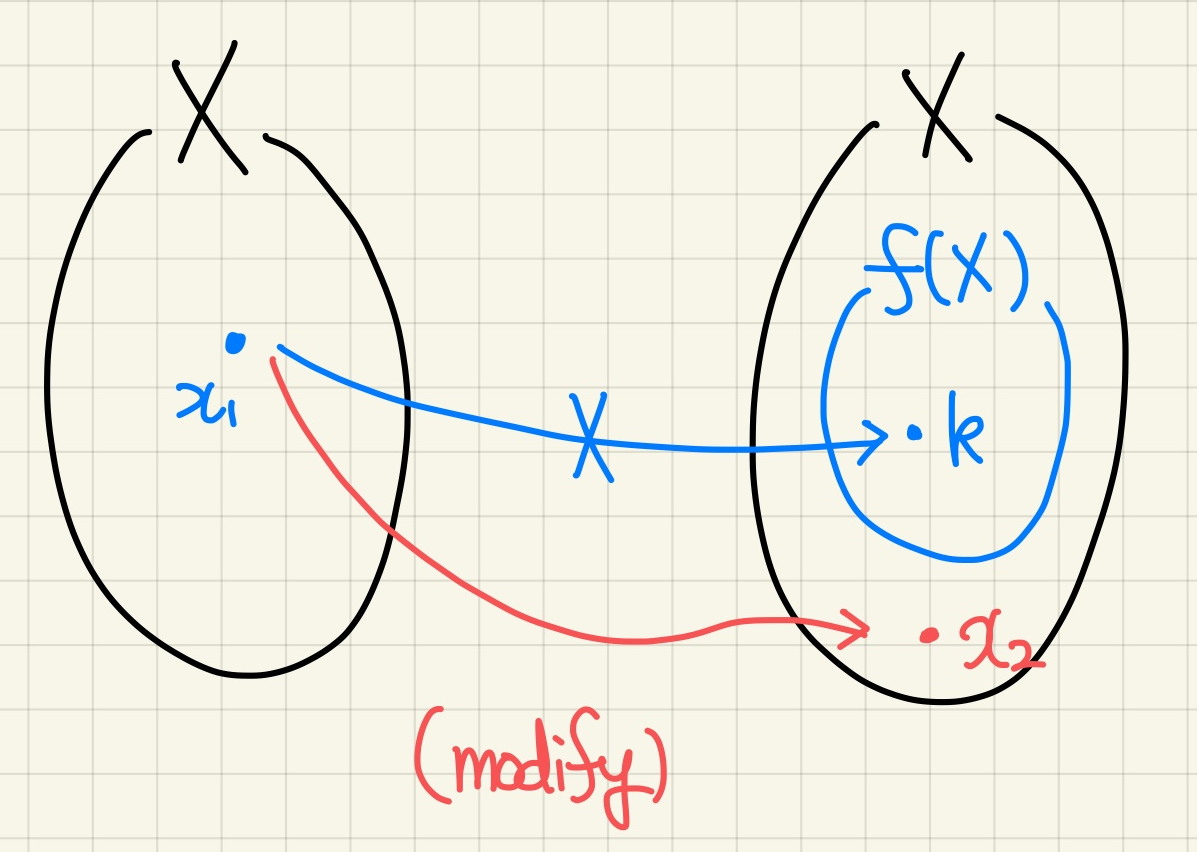
정리($S.T$) 4.3) 무한집합에서 원소를 유한개 제거해도 여전히 무한집합이다.
$X$ 가 무한집합이면 $X$ 의 임의의 원소 $k$ 에 대하여 $X-\left\{ k \right\}$ 는 무한집합이다.
증명) $X$가 무한집합이므로, $f(X)\neq X$ 인 단사함수 $f:X\rightarrow X$ 가 존재한다. 임의의 $k\in X$ 에 대하여, $k\in f(X)$ 와 $x\in X-f(X)$ 인 경우로 나누어 보자.
i) $k\in X-f(X)$ 일 때 : 이는 쉽게 말해 $k\notin f(X)$ 라는 뜻이다.$g:X-\left\{ k \right\}\rightarrow X-\left\{ k \right\}$ 를 $g(x)=f(x)$ 로 정의하자. 원래 함수의 공역을 함부로 줄이면 안되는데, $f(x)=k$ 가 되는 $x\in X-\left\{ k \right\}$ 가 i) 의 가정 상황에서는 존재하지 않기 때문에 $g$ 는 잘 정의된다(well-defined).
한편 $f$ 가 단사이므로, $g$ 또한 단사이기에 $g(X-\left\{ k \right\})=g(X)-g(k)$ 가 되고,
$$\begin{align*}
g(X-\left\{ k \right\})&=g(X)-g(k)
\\\\&=f(X)-f(k) \subset
X-\left\{ k \right\}
\end{align*}$$
이므로 $g(X-\left\{ k \right\})\neq X-\left\{ k_0 \right\}$ 가 된다. 따라서 $X-\left\{ k \right\}$ 는 무한집합이다.
ii) $k\in f(X)$ 일 때 : $g:X-\left\{ k \right\}\rightarrow X-\left\{ k \right\}$ 가 잘 정의되지 않는다. $f(x_1)=k$ 를 만족하는 $x_1\in X-\left\{ k \right\}$ 가 존재할 수 있기 때문이다. 그러므로 $g:X-\left\{ k \right\}\rightarrow X-\left\{ k \right\} $ 를 다음과 같이 i) 에서와 달리 수정하자 :
$$g(x) = \left\{ \begin{array}{cl}
f(x) & \;\; \ x \neq x_1 \\
x_2 & \;\; \ x=x_1 \in X-\left\{ k \right\}
\end{array} \right.$$
여기서 $x_2$ 는 $x_2\in X-f(X)$ 인 어떤 원소를 택한 것이다. 그러면, $g:X-\left\{ k \right\}\rightarrow X-\left\{ k \right\} $ 는 잘 정의되고 단사이다.
한편
$$\begin{align*}
g(X-\left\{ k \right\})&=f(X-\left\{ k,x_1 \right\})\cup \left\{ x_2 \right\}
=f(X)- f(k)\cup x_2 \\\\&= f(X)- f(k)\cup x_2 \subset X-\left\{ k \right\}
\end{align*}$$
가 성립한다. (마지막 식은) 왜냐하면 $f(k)\in X-\left\{ k \right\}$ 이지만 $f(k) \notin g(X-\left\{ k \right\})$ 이기 때문이다. 따라서 $ g(X-\left\{ k \right\})\subseteq X-\left\{ k \right\}$ 가 되어 $X-\left\{ k \right\}$ 는 무한집합이다. $_\blacksquare$
정리($S.T$) 4.4)
각각의 $k\in\mathbb{N}$ 에 대하여, $\mathbb{N}_k$ 는 유한집합이다.
증명) 수학적 귀납법을 이용하자. $k=1$ 일 때 $\mathbb{N}_1=\left\{ 1 \right\}$ 이므로 유한집합이다. 이제 $n=k$ 일 때 $\mathbb{N}_k$ 가 유한집합이라고 가정하자. $\mathbb{N}_{k+1}=\mathbb{N}_{k}\cup \left\{ k+1 \right\}$ 가 유한집합임을 증명해야 하는데, 이것이 무한집합이라고 가정하면 위의 정리($S.T$) 4.3) 에 의하여 $\mathbb{N}_{k}\cup \left\{ k+1 \right\}-\left\{ k+1 \right\}=\mathbb{N}_k$ 또한 무한집합이 되어, 가정에 모순이다. 따라서 $\mathbb{N}_{k+1}$ 은 유한집합이고, 모든 $k\in\mathbb{N}$ 에 대해 $\mathbb{N}_k$ 는 유한집합이다. $_\blacksquare$
정리($S.T$) 4.5) 유한집합의 정의
집합 $X$ 가 유한집합일 필요충분조건은 $X=\phi$ 이거나 $X$ 와 $\mathbb{N}_k$ 사이에 일대일대응이 존재하는 것이다. 다시 말해, 오직 이 두 경우에만 $X$ 가 유한집합이고 그렇지 않은 모든 경우에 $X$ 는 무한집합이다.
증명)
$\Rightarrow$ : 우선 예제 2)에 의하여 $X=\phi$ 이면 $X$는 유한집합이다. 또한 정리($S.T$) 4.4)가 참이므로, 이의 대우명제를 생각하면 공역 $\mathbb{N}_k$ 이 유한집합이므로 반드시 $X$ 는 유한집합이 되어야 한다.
$\Leftarrow$ : 역을 증명할 때 역의 대우명제를 증명하자. 이는 만일 $X$와 $\mathbb{N}_k$ 사이에 일대일대응이 존재하지 않으면 $X$가 무한집합이라는 것이다.
$X$ 가 $\mathbb{N}_k$ 와 일대일대응이 존재하지 않는다고 가정하고 $x_1\in X$ 를 하나 택하자. 그러면 $X-\left\{ x_1 \right\}\neq \phi$ 인데, 만일 그렇지 않다면 $ X=\left\{ x_1 \right\}$ 이므로 $\mathbb{N}_1$ 과 일대일대응이 존재하므로 가정에 모순이기 때문이다. 이 방법을 계속 반복하면, $X-\left\{ x_1,x_2,\cdots ,x_k \right\}$ 는 공집합이 아니다. 만일 공집합이면 $X=\left\{ x_1,x_2,\cdots ,x_n \right\}$ 이고 $X$ 와 $\mathbb{N}_k$ 사이에 일대일대응이 존재하게 되기 때문이다. 그러면 $X-\left\{ x_1,x_2,\cdots ,x_n \right\}$ 에서 언제나 원소 $x_{k+1}\in X-\left\{ x_1,x_2,\cdots ,x_k \right\}$ 을 택할 수 있고, 그러므로 수학적 귀납법에 따라 각각의 자연수 $n$ 에 대하여 $X$ 의 진부분집합 $Y=\left\{ x_n\mid n \in\mathbb{N} \right\}=\left\{ x_1,x_2,\cdots \right\}$ 이 항상 존재한다.
이제 함수 $f:Y\rightarrow Y$ 를 모든 $k\in\mathbb{N}$ 에 대하여 $f(x_k)=x_{k+1}$ 로 정의하자. 그러면 $x_1\notin f(Y)$ 가 되므로 공역을 축소해서 함수를 $f: Y\rightarrow Y-\left\{ x_1 \right\}$ 로 바꾸어도 $f$ 는 일대일대응이다. 이는 $Y$ 가 그것의 진부분집합과 일대일대응이 존재하는 상황이니 $Y$ 는 정의 ($S.T$) 4-1) 에 의하여 무한집합이다. 그런데 $Y\subseteq X$ 이므로 정리($S.T$) 4.1)-① 에 의하여 초집합 $X$ 또한 무한집합이다. $_\blacksquare$
그래서 결국 유한집합과 무한집합을 구분하는 기준은 우리가 처음에 세웠던 정의($S.T$) 4-1) 뿐만 아니라, 위 정리를 사용해도 좋습니다. 즉 항상 무한집합임을 보이기 위해 주어진 집합의 진부분집합과 일대일대응을 만들지 않아도, $\mathbb{N}_k$ 와 일대일대응이 존재하는지를 대신 살펴볼 수 있습니다. 그러하다면 유한집합이니 무한집합이 아니라고 판단할 수 있는 것입니다.
[참고문헌]
You-Feng Lin, Shwu-Yeng T,Lin - Set thoery
- 실생활에서 분수를 통해 개수를 표현하기도 하긴 하지만, 개수의 의미를 생각해보면 소수(decimal)를 통한 개수 표현은 그리 적절하지 않습니다. 예컨대 사과가 '3.5개' 있다는 표현은 3개가 있고 반쪽짜리가 1개 있다는 것을 의미하는 것이지 동일한 형태의 사과가 3.5개 있다는 뜻이 아닙니다. 고로 여기서 소수 표현 0.5는 사과의 양이 1에 비해 0.5만큼 있다는 것을 나타내는 표현이지, 개수로만 따지면 엄연히 3개가 있고 반쪽자리 1개가 있으니 4덩이, 즉 4개가 있는 셈입니다. 여기서 우리가 말하고자 하는 '개수'는 '덩이'의 표현에 가깝다는 뜻입니다. [본문으로]
- 실제로 무한집합을 나타낼 때 단순히 이렇게 수식으로 쓰면 오해의 여지가 있습니다. 농도 개념을 자세히 다루기 전에 한하여 이런 표현을 편의상 도입하겠다는 뜻입니다. [본문으로]
- 단 하나만 존재함을 보여도 충분합니다. [본문으로]
- 일반적으로 유한집합 사이에서 일대일대응은 $f(X)=X$ 이지만, $X$ 가 무한집합이기 때문에 $f(X)\neq X$ 이면서 일대일대응인 단사함수 $f$ 를 잡을 수 있는 것입니다. [본문으로]
'집합론(Set Theory) > 기수론' 카테고리의 다른 글
| 기수의 덧셈과 곱셈(Addition and product of cardinal number) (2) | 2023.11.27 |
|---|---|
| 칸토어의 정리(Cantor's Theorem) (0) | 2023.11.26 |
| 집합의 기수와 칸토어-슈뢰더-베른슈타인 정리(Cardinal number of set and Cantor-Schröder-Bernstein Theorem) (1) | 2023.11.26 |
| 칸토어의 대각선 논법으로 실수가 비가부번집합임을 보이기(Real number is nondenumerable by using Cantor's diagonal method) (1) | 2023.11.25 |
| 가부번집합과 가산집합(Denumerable and countable set) (1) | 2023.11.25 |




댓글