가부번집합과 가산집합(Denumerable and countable set)

무한집합에 대한 논의를 마쳤기 때문에 이제 본격적으로 집합의 원소를 어떻게 셀 지에 대해 연구해 보려고 합니다.

---

1. 집합의 대등

 

정의($S.T$) 4-2) 집합의 대등
두 집합 $X,Y$ 에 대하여 일대일대응 $f:X\rightarrow Y$ 가 존재할 때, $X$와 $Y$는 '대등(Equipotent)'하다고 하며 $X\sim Y$ 로 나타낸다.
$f:X\rightarrow Y$ 에 대해 $X$ 와 $Y$ 가 대등하면, 간단히 $f:X\sim Y$ 로 표기한다.

 

일대일 대응을 만들 수 있는 두 집합 사이의 관계를 대등이라고 정의합니다. 예를 하나 들어보자면 $\mathbb{N}$ 과 $\mathbb{N}-\left\{ 1 \right\}$ 은 같은 집합이 아니지만, 일대일대응인 함수를 만들 수 있으므로 대등합니다. 즉 집합이 같다는 개념과 대등하다는 개념은 차이가 있으니 구분해야 합니다. 다음과 같이 정리할 수 있습니다.

 

 

정리($S.T$) 4.6) 집합의 상등과 대등의 차이
공집합이 아닌 두 집합 $A,B$ 에 대하여 $A=B$ 이면 $A\sim B$ 이다. 하지만 역은 (항상) 성립하지(는) 않는다. $A\subseteq B$ 인 경우에도 $A\sim B$ 일 수 있다.

 

집합론에서 대등(equipotent)의 개념과 아래 두 예제는 집합론의 지금 주제에서 뿐만 아니라, 나중에 위상수학에 가서 위상동형을 포함한 전반적인 개념을 다룰 때 매우 매우 중요합니다. 특히 아래 예제 둘은 반드시 기억해야만 하는 성질로서 함수까지 아예 암기하는 것을 권합니다.

---

예제 1) $(0,1)$ 과 $(-1,1)$ 는 대등한가?

 

sol) 대등하다. 두 열린구간을 연결하는 일대일대응인 함수를 고려하면 된다. 가장 간단한 것으로 일차함수 $y=2x-1$ 을 떠올릴 수 있다. 다만 이 함수가 유일한 것은 아니며, $0 < x < 1$ 에서 $y=x$ 를 지나지 않는 단조증가함수를 적절히 고르면 모두 일대일대응을 만들 수 있다.

 

 

예제 2) $(-1,1)$ 과 $\mathbb{R}$ 은 대등한가?

 

sol) 대등하다. $(-1,1)$ 에서 $f(x)=\tan \left( \displaystyle\frac{\pi x}{2} \right)$ 으로 이 함수 $f:(-1,1)\rightarrow \mathbb{R}$ 은 단사이고 전사이다.

 

[그림 1] Desmos 를 이용해서 주어진 함수의 그래프를 그린 것.

 

---

 

정리($S.T$) 4.7) 대등은 동치관계다
집합족 $P$ 위에서, 임의의 두 원소 $X,Y\in P$ 에 대해 관계 $\mathcal{R}$ 이 $X\mathcal{R}Y$ 로 주어질 필요충분조건은 $X\sim Y$ 인 것이다. 즉, 대등이 $\mathcal{R}$ 로 주어지면 이는 $P$ 위의 하나의 동치관계가 된다.
따라서 공집합이 아닌 집합 $X,Y$ 에 대하여
① $X\sim X$
② $X\sim Y \; \Leftrightarrow \; Y\sim X$
③ $X\sim Y$ 이고 $Y\sim Z$ 이면 $X\sim Z$ 이다.

 

결론은 대등이 동치관계가 된다는 것입니다. 그 까닭은 당연히 대등이라는 관계가 반사율, 대칭률, 추이율을 만족하게 되기 때문입니다. 이들을 보이는 것은 간단하므로 증명 과정을 생략하겠습니다.

 

 

정리($S.T$) 4.8) 
서로소인 집합들의 원소들로 구성된 두 첨수집합족 $\left\{ X_\gamma \mid \gamma\in \Gamma \right\}$ 와 $\left\{ Y_\gamma \mid \gamma\in \Gamma \right\}$ 을 생각하자. 각 $\gamma$ 에 대해 $X_\gamma\sim Y_\gamma$ 이면 $\displaystyle \bigcup_{\gamma\in\Gamma}^{}X_\gamma \sim \displaystyle \bigcup_{\gamma\in\Gamma}^{}Y_\gamma$ 이다.

따름정리($S.T$) 4.8.1)
네 집합 $X,Y,Z,W$ 에 대하여 $X\cap Z=Y\cap W=\phi$ 이고 $f:X\sim Y\, , \, g:Z\sim W$ 이면 $f\cup g: (X\cup Z)\sim (Y\cup W)$ 이다.

증명) 각각의 $\gamma\in \Gamma$ 에 대하여 $X_{\gamma} \sim Y_{\gamma}$ 이므로, 각각의 $\gamma\in \Gamma$ 에 대하여 전단사함수 $f_{\gamma}:X_{\gamma}\sim Y_{\gamma}$ 가 존재한다. 또한 각각의 $\gamma\in\Gamma$ 에 대하여 $X_{\gamma}$ 와 $Y_{\gamma}$ 들이 모두 서로소이므로, $f_{\gamma}$ 함수들 각각의 정의역과 공역 또한 서로소이다.

이때 $f_{\gamma}$ 들의 합집합으로 구성된 함수 $h:\displaystyle \bigcup_{\gamma\in\Gamma}^{}X_{\gamma} \rightarrow \displaystyle \bigcup_{\gamma\in\Gamma}^{}Y_{\gamma}$ 를 $x\in X_{\gamma}$ 이면 $h(x)=f_{\gamma} (x)$ 인 것으로 정의하자.

i) 잘 정의됨 : $x_1=x_2\in \displaystyle \bigcup_{\gamma\in\Gamma}^{}X_{\gamma}$ 라 가정하자. 그러면 어떤 $\gamma\in\Gamma$ 에 대하여 $h(x_1)=f_{\gamma}(x_1)$ 이고 $h(x_2)=f_{\gamma}(x_2)$ 가 된다. 그런데 $x_1=x_2$ 이므로 공통적으로 어떤 $\gamma \in \Gamma$ 에 대하여 $x_1,x_2\in X_{\gamma}$ 이 성립한다. 그리고 모든 $X_{\gamma}$ 는 서로소이므로, 결국 $f_{\gamma}(x_1)=f_{\gamma}(x_2)$ 이다.

ii) $h$ 는 단사이다 : 어떤 $x_1,x_2\in \displaystyle \bigcup_{\gamma\in\Gamma}^{}X_{\gamma}$ 에 대하여 $h(x_1)=h(x_2)$ 라 가정하자. 그러면 $\gamma_1,\gamma_2\in \Gamma$ 에 대하여 $f_{\gamma_1}(x_1)=f_{\gamma_2}(x_2)$ 가 된다. 그런데 $X_{\gamma_1}$ 과 $X_{\gamma_2}$ 가 서로소이고 모든 $f_{\gamma}$ 들이 단사이므로, $\gamma_1=\gamma_2$ 와 $x_1=x_2$ 가 성립한다. 따라서, $h$ 도 단사이다.

iii) $h$ 는 전사이다 : $y\in\displaystyle \bigcup_{\gamma\in\Gamma}^{}Y_{\gamma}$ 라 하자. 그러면 $y\in Y_{\gamma}$ 가 되는 $\gamma\in\Gamma$ 가 존재한다. $f_{\gamma}$ 가 전사함수이므로, $y=f_{\gamma}(x)$ 가 되는 $x\in X_{\gamma}$ 가 존재한다. 따라서 $y=h(x)$ 로 정의하면 $h$ 역시 전사이다.

서로 다른 $\gamma$ 가 두 개 뿐인 경우가 따름정리의 상황이다. $_\blacksquare$

 

 

 

정리($S.T$) 4.9)
네 집합 $X,Y,Z,W$ 에 대하여 $X\sim Y$ 이고 $Z\sim W$ 이면 $\left( X\times Z \right) \sim \left( Y\times W \right)$ 이다.

증명) $f:X\sim Y$, $g:Z\sim W$ 라 하자. 그러면 함수 $f\times g : X\times Z \rightarrow Y\times W$ 를, 모든 $(x,z)\in X\times Z$ 에 대하여 $(f\times g)(x,z)=(f(x),g(z))$ 가 되도록 정의하자.

1) $f\times g$ 는 단사인가?
$(f\times g)(x_1,z_1)=(f\times g)(x_2,z_2)$, 곧 $(f(x_1),g(z_1))=(f(x_2),g(z_2))$ 라 가정하자. 두 순서쌍이 같으려면 같은 위치의 순서쌍 성분끼리 같으면 되므로 $f(x_1)=f(x_2)$ 이고 $g(z_1)=g(z_2)$ 이다. 그런데 $f,g$ 가 전단사이므로 당연히 단사이고, 따라서 $x_1=x_2$ 이고 $z_1=z_2$ 가 된다. 고로 $(x_1,z_1)=(x_2,z_2)$ 가 성립하여, $f\times g$ 는 단사이다.

2) $f\times g$ 가 전사인가?
모든 $(f(x),g(z))\in (Y\times W)$ 에 대하여 $(f\times g)(x,z)=(f(x),g(z))$ 가 되게하는 $(x,z)\in X\times Z$ 가 존재하는지를 보이면 된다. $(f(x),g(z))\in (Y\times W)$ 이므로 $f(x)\in Y\,,\, g(z)\in W$ 인데, $f,g$ 는 모두 전사이므로 모든 $y,w$ 에 대해 각각 $y=f(x)\,,\, w=g(z)$ 가 되게 하는 $x\in X$ 와 $z\in Z$ 가 존재한다. 따라서 $(x,z)\in X\times Z$ 가 존재하여 $f\times g$ 는 전사이다.

고로 $f\times g$ 는 전단사이므로, $X\times Z\sim Y\times W$ 가 성립한다. $_\blacksquare$

 

---

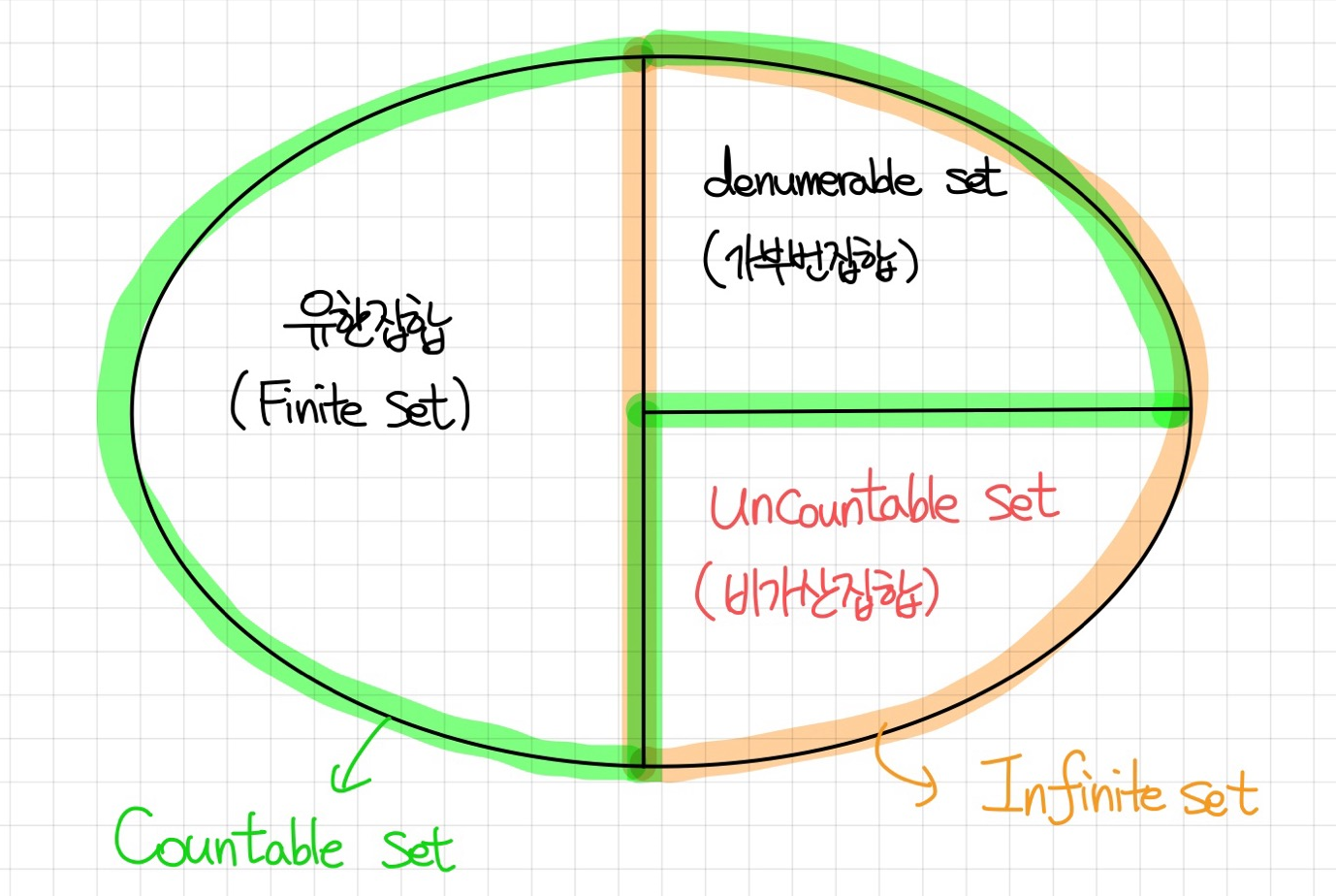
2. 가부번집합과 가산집합

 

이제 가부번집합과 가산집합을 정의합니다.

 

정의($S.T$) 4-3) 가부번집합과 가산집합
① 집합 $X$ 가 '가부번집합(denumberable set)'이라는 것은, 다시 말해 '번호를 붙일 수 있다(=가부번)(denumberable)'는 것은 $X\sim \mathbb{N}$ 임을 가리킨다.
반면 $X$ 가 '비가부번집합(nondenumerable set)'이라는 것은 $X$ 가 무한집합이면서 가부번집합이 아닐 때를 말한다.

② 주어진 집합이 유한집합이거나 가부번집합이면 이를 '가산집합(countable set)'이라 하고 간단히 '셀 수 있다(countable)'이라 표현한다.
가산집합이 아닌 것은 '비가산집합(uncountable set)'이라 한다.

 

즉 자연수 집합과 대등하면, 곧 일대일대응을 만들 수 있으면 그 집합은 가부번집합입니다. 자연수는 $1,2,3,\cdots$ 이니 자연수 집합과 일대일대응을 만들 수 있다는 것은 곧 번호를 붙일 수 있다는 것과 같습니다. 반면 셀 수 있다는 것은 주어진 집합이 유한집합이거나, 무한집합인데 가부번집합인 것을 말합니다.

 

주의할 점은 가부번집합과 가산집합에 부정을 붙일 때입니다.

가산집합의 부정은 비가산집합입니다. 비가산집합은 무조건 무한집합이지요. 하지만 무한집합 중에서는 가부번집합도 있고 비가부번집합도 있습니다. 이 중(무한집합 중) 비가부번집합은 비가산집합이 되지만, 단순히 가부번집합의 부정은 유한집합 또는 비가부번집합이니 가산집합일수도, 비가산집합일 수도 있습니다.  말이 은근 헷갈리므로 이를 벤 다이어그램으로 간단히 나타낸 아래 그림을 참고해 보도록 합시다.

 

정의에 의하면 사실 유한집합이 아닌(무한집합인) 비가부번집합은 비가산집합과 필요충분조건 관계입니다.

 

[그림 2] 가산, 가부번, 유한과 무한집합을 벤 다이어그램으로 나타낸 것.

 

 

정리($S.T$) 4.10) 가부번의 부분집합은 가부번이다.
임의의 무한집합 $A$ 가 가부번집합 $B$ 의 부분집합, 즉 $A\subseteq B$ 라고 하자. 그러면 $A$ 도 가부번집합이다.

따름정리($S.T$) 4.10.1)
모든 가산집합의 부분집합은 가산집합이다.

증명) 가부번집합을 $B=\left\{ b_1,b_2,b_3,\cdots \right\}$ 이라 놓고 $B$ 의 무한집합인 부분집합을 $A$ 라 하자. 즉 $A\subseteq B$ 이다.
그러면 $A$ 의 원소는 $b_1,b_2,\cdots$ 중 일부로 구성되어 있다. 그 중 첨자가 가장 작은 것을 $n_1$, 곧 $b_{n_1}\in A$ 라 하자. 그 다음 $A-\left\{ a_{n_1} \right\}$ 의 원소 중 첨자가 가장 작은 것을 $n_2$ 로 하여 $b_{n_2}\in A-\left\{ a_{n_1} \right\}$ 라 하자. 이를 반복하여 $k\in \mathbb{N}$ 에 대해 $b_{n_{k}} \in A$ 를 정의하고, $n_{k+1}$ 가 $b_{n_{k+1}} \in A-\left\{ b_{n_1},b_{n_2},\cdots ,b_{n_{k}}  \right\}$ 가 되도록 하자. $A$ 가 무한집합이기 때문에, 그러한 $b_{n_{k+1}}$ 은 각각의 $k\in\mathbb{N}$ 에 대해 항상 존재한다. 
그러면 함수 $g:\mathbb{N}\rightarrow A$ 을 각각의 $k\in \mathbb{N}$ 에 대해 $g(k)=b_{n_k}$ 로 정의할 수 있고, 이는 일대일대응이 된다. 고로 $g:\mathbb{N}\sim A$ 가 되어, $A$ 는 가부번(denumerable)이다. $_\blacksquare$

따름정리의 증명은 생략한다.

 

 

정리($S.T$) 4.11) 가산의 합집합은 가산이다.
① 임의의 두 가부번집합 $A,B$ 에 대해 $A\cup B$ 도 가부번집합이다.
② 임의의 두 유한집합 $A,B$ 에 대해 $A\cup B$ 는 가산집합이다.
위 두 명제를 통합하면 임의의 두 가산집합 $A,B$ 에 대해 $A\cup B$ 는 가산집합이다.

따름정리($S.T$) 4.11.1)
$A_1,A_2,\cdots , A_n$ 이 모두 가부번집합이라고 하자. 그러면 $\displaystyle \bigcup_{k=1}^{n}A_k$ 도 가부번집합이다.

증명)
① 두 가지 경우로 나누어 증명하자.

1) $A\cap B=\phi$
홀수의 자연수 집합과 짝수의 자연수 집합을 각각 $\mathbb{N}_o\,,\, \mathbb{N}_e$ 라 하자. $A\sim \mathbb{N}$ 이고 $\mathbb{N}\sim \mathbb{N}_o$ 이므로 $\sim$ 의 동치관계 추이성으로 인해 $A\sim \mathbb{N}_o$ 이다. 유사하게, $B\sim \mathbb{N}_e$ 이다. 그러면 따름정리($S.T$) 4.8.1) 에 의하여 $(A\cup B)\sim (\mathbb{N}_o\cup \mathbb{N}_e) =\mathbb{N}$ 이다. 그러면 $(A\cup B)\sim \mathbb{N}$ 이 되므로 $A\cup B$ 는 가부번집합이다.

2) $A\cap B\neq \phi$ 
$C=B-A$ 라 하자. $A\cup C = A\cup B$ 이고 $A\cap C=\phi$ 이다. 여기서 집합 $C$ 는 $C\subseteq B$ 이므로 따름정리($S.T$) 4.10.1) 에 의하여 유한집합 또는 가부번집합이다. 
만일 $C$ 가 유한집합이면 $A\cup C = A\cup B$ 는 가부번집합이다. 만일 $C$ 가 가부번집합이면 1)에 의해 $A\cup C = A\cup B$ 또한 가부번집합이다.

② 가산집합의 정의에 해당하여 사실 증명할 것이 없다. 임의의 두 유한집합 $A,B$ 의 합집합도 유한집합이니, 가산집합이다. $_\blacksquare$

따름정리의 증명) $A_1, A_2$ 가 가부번집합일 때, 수학적 귀납법을 사용하자.

1) (Base step) $n=1$ : $A_1\cup A_2$ 는 ②에 의해 가부번집합이다.
2) (Inductive step) $n=m$ : $m\in\mathbb{N}$ 일 때 $\displaystyle \bigcup_{k=1}^{m}A_k$ 이 가부번집합이라고 가정하자.
$n=m+1$ 일 때 $\displaystyle \bigcup_{k=1}^{m+1}A_k$ 이 가부번집합임을 보이고 싶다. 두 가부번집합의 합집합이 가부번집합임을 알고 있으므로, Inductive step 에 의해 $\displaystyle \bigcup_{k=1}^{m}A_k$ 이 가부번이고 새로운 가부번집합 $A_{m+1}$ 에 대해 $\displaystyle \bigcup_{k=1}^{m}A_k\cup A_{m+1}=\displaystyle \bigcup_{k=1}^{m+1}A_k$ 또한 가부번집합이다. $_\blacksquare$

 

 

 

정리($S.T$) 4.12) 정의역이 가산집합이면, 치역도 가산집합이다.
집합 $Y$와 함수 $f:\mathbb{N}\rightarrow Y$ 를 생각하자. 그러면 치역(image) $f(\mathbb{N})\subseteq Y$ 은 가산집합이다.

따름정리($S.T$) 4.12.1)
집합 $X$가 가산집합일 때 함수 $f:X\rightarrow Y$ 에 대하여 치역(image) $f(X)\subseteq Y$ 는 가산집합이다.

증명) $f(\mathbb{N})$ 이 가산집합임을 보이기 위해서는 $f(\mathbb{N})=\left\{ y\in Y \mid y=f(n)\;\text{for some}\;n\in\mathbb{N} \right\}$ 의 원소들이 각각 자연수의 하나의 원소와 대응된다는 사실을 보여주면 된다. $f:\mathbb{N}\rightarrow Y$ 를 $f(n)=n\in\mathbb{N}$ 으로 정의하면 $f(1),f(2),\cdots$ 은 $n=1,2,\cdots$ 와 자연스럽게 대응되므로 $f(\mathbb{N})\subset Y$ 이고 $f$ 는 단사이므로, 결국 일대일대응이된다. 따라서 $\mathbb{N}\sim f(\mathbb{N})$ 이 되므로, $f(\mathbb{N})$ 은 가산집합이다. $_\blacksquare$

 

 

이를 활용해서 자연수보다 큰 수 체계에 대해 가부번성을 조사해 볼 수 있습니다.

---

예제 4) 정수집합 $\mathbb{Z}$ 는 가부번집합인가?

 

sol) $\mathbb{Z}\sim \mathbb{N}$ 이 성립하는지를 보면 된다. 자연수 집합은 이미 가산집합임을 알고 있어서, 집합 $-\mathbb{N}$ 을 

$$-\mathbb{N}:=\left\{ -n\mid n\in\mathbb{N} \right\}=\left\{ 0,-1,-2,\cdots \right\}$$

으로 정의하자. (그러니까 여기선 $0 \in \mathbb{N}$ 인 것으로 취급한다)그러면 $g:\mathbb{N}\rightarrow -\mathbb{N}$ 을 $g(n)=-n$ 으로 정의하면 $g$ 는 일대일대응이 되므로, $-\mathbb{N}$ 도 가산집합이 된다. 그러면 $\mathbb{Z}=-\mathbb{N}\cup\mathbb{N}$ 이 되므로 정리 ($S.T$) 4.11) 에 의하여 $\mathbb{Z}$ 또한 가부번집합이고, 고로 가산집합이다. $_\blacksquare$

정리($S.T$) 4.13)
집합 $\mathbb{N}\times \mathbb{N}$ 은 가부번집합이다. 다시 말해 $\left( \mathbb{N}\times \mathbb{N} \right)\sim \mathbb{N}$ 이다.

따름정리($S.T$) 4.13.1)
집합 $X,Y$ 가 가산집합이면 $X\times Y$ 또한 가산집합이다.

따름정리($S.T$) 4.13.2)
$\mathbb{N}\times \mathbb{Z}\;,\;\mathbb{Z}\times \mathbb{Z}$ 등등도 모두 가산집합이다.

증명) 함수 $f:\mathbb{N}\times \mathbb{N} \rightarrow \mathbb{N}$ 을 $f(n,m)=2^n3^m$ 으로 정의하자. 

$f$는 단사이고 잘 정의된다 : 
$$\begin{align*} f(n,m)=f(n',m')&\Leftrightarrow 2^n3^m = 2^{n'}3^{m'} \\\\ &\Leftrightarrow2^{n-n'}=3^{m-m'}\\\\ &\Leftrightarrow n-n'=0\;\;\text{and}\;\; m-m'=0 \\\\ &\Leftrightarrow n=n' \;\; \text{and} \;\; m=m' \end{align*}$$
전사일 필요가 없이, 일단 $\mathbb{N}\times \mathbb{N} \sim f(\mathbb{N}\times \mathbb{N})$ 이 되고, (왜냐하면 공역인 $\mathbb{N}$ 과 대등하다는 것이 아니라 치역과 대등하다는 것이니), $f(\mathbb{N}\times \mathbb{N})\subseteq \mathbb{N}$ 이 된다. 이때 $\mathbb{N}\times \mathbb{N}$ 이 무한집합이므로, 정리($S.T$) 4.2) 에 의하여 $f(\mathbb{N}\times \mathbb{N})$ 또한 무한집합이 된다. 그런데 $f(\mathbb{N}\times \mathbb{N})$ 이 가부번집합인 자연수 집합의 부분집합이므로 정리 ($S.T$) 4.10) 에 의하여 가부번집합이다. 즉, $\mathbb{N}\sim f(\mathbb{N}\times \mathbb{N})$ 이라는 뜻이고, 위에서 $f(\mathbb{N}\times \mathbb{N})\sim \mathbb{N}\times \mathbb{N}$ 였으니, $\sim$ 은 동치관계이므로 추이성에 의해 $\mathbb{N}\times \mathbb{N} \sim \mathbb{N}$ 이다. 따라서 $\mathbb{N}\times \mathbb{N}$ 은 가부번집합이다. $_\blacksquare$

따름정리의 증명) 

1) $X,Y$ 가 유한집합인 경우 : 유한집합의 합집합도 유한집합이므로 가산집합임은 자명하다. 정리 $(S.T)$ 4.11) 에서 이미 다루었다.

2) $X,Y$ 가 가부번집합인 경우를 고려하자. 그러면 두 함수 $f:X\sim \mathbb{N}$ 과 $g: Y\sim \mathbb{N}$ 이 존재한다. 이때 함수 $h:(X\times Y)\rightarrow (\mathbb{N}\times \mathbb{N})$ 을 $(x,y)\mapsto (n,m)=(f(x),g(y))$ 으로 정의하고 이것이 전단사임을 보이면, 위의 정리에 따라 따름정리가 증명된다.

i) $h$ 는 전사이다 : 임의의 $(n,m)\in \mathbb{N}\times \mathbb{N}$ 에 대하여, $f,g$ 는 전사이므로 $f(x)=n\;,\;g(y)=m$ 를 만족시키는 $(x,y)\in (X\times Y)$ 가 존재한다.

ii) $h$ 는 단사이다 : $f,g$ 가 단사라는 것을 마지막 $\Rightarrow$ 에서 적용하면 $h$ 또한 단사임을 쉽게 확인할 수 있다.

$$\begin{align*} h(x,y)=h(x',y')\;&\;\Rightarrow \; (n,m)=(n',m') \\\\&\;\Rightarrow \; n=n'\;,\;m=m' \\\\&\;\Rightarrow \; f(x)=f(x')\;\wedge \; g(y)=g(y') \\\\&\;\Rightarrow \;x=x'\;\wedge \;y=y' \\\\&\;\Rightarrow \; (x,y)=(x',y') \;\;\;\;\;_\blacksquare \end{align*}$$

 

 

 

정리($S.T$) 4.14)
각각의 $k\in\mathbb{N}$ 에 대하여 $A_k$ 는 가부번집합이고 $A_j\cap A_k = \phi\;\;(j\neq k)$ 이면 $\displaystyle \bigcup_{k\in\mathbb{N}}^{}A_k$ 는 가부번집합이다.
사실 $A_j\cap A_k \neq \phi\;\;(j\neq k)$ 이어도 주어진 명제는 참이다.

증명) 각각의 $k\in \mathbb{N}$ 에 대하여, 함수 $f_k : \mathbb{N}\rightarrow \mathbb{N}\times \left\{ k \right\}$ 를 모든 $j\in\mathbb{N}$ 에 대하여 $f_k(j):= (j,k)$ 로 정의하자.

1) $f_k$ 는 단사이고 잘 정의된다 : 

$$\begin{align*} f_k(j_1)=f_k(j_2)&\Leftrightarrow (j_1,k)=(j_2,k) \\\\&\Leftrightarrow j_1=j_2\;\;,\;\;k=k(\text{trivial}) \end{align*}$$

2) $f_k$ 는 전사이다 : 각각의 (정해진) $k\in\mathbb{N}$ 에 대해, 모든 $(j,k)\in \mathbb{N}\times \left\{ k \right\}$ 에 대하여 $f_k(j)=(j,k)$ 를 만족하는 자연수 $j\in \mathbb{N}$ 이 존재한다.

그러므로 각각의 $k\in\mathbb{N}$ 에 대해 $f_k$ 는 전단사가 되어, $\mathbb{N}\sim \mathbb{N}\times \left\{ k \right\}$ 가 된다. 게다가 우리의 가정에 의해 각각의 $k\in \mathbb{N}$ 에 대해 $A_k$ 는 가부번집합이므로 $A_k\sim \mathbb{N}$ 이고, 대등의 동치관계 추이성에 의해 $A_k\sim \left( \mathbb{N}\times \left\{ k \right\} \right)$ 이다. 그러면 정리 ($S.T$) 4.8) 에 의해 $\displaystyle \bigcup_{k\in\mathbb{N}}^{}A_k\sim \displaystyle \bigcup_{k\in\mathbb{N}}^{}\mathbb{N}\times \left\{ k \right\}$ 이 성립하고, $\displaystyle  \bigcup_{k\in\mathbb{N}}^{}\mathbb{N}\times \left\{ k \right\} = \mathbb{N}\times \mathbb{N}$ 이므로 $\left( \displaystyle \bigcup_{k\in\mathbb{N}}^{}\mathbb{N}\times \left\{ k \right\} \right)\sim (\mathbb{N}\times \mathbb{N})$ 으로부터 $\displaystyle \bigcup_{k\in\mathbb{N}}^{}A_k$ 는 가부번집합이다.

만일 $A_j\cap A_k \neq \phi\;\;(j\neq k)$ 인 경우를 생각해보자. $A_j\cap A_k =B_i\neq \phi\;\;(j\neq k)$ 라 해보자. 그러면 $A_j-B_i$ 는 여전히 가부번집합이고, $(A_j-B_i)\cap A_k = \phi\;\;(j\neq k)$ 가 된다. 그러므로 위의 논리를 그대로 적용할 수 있다. $_\blacksquare$

 

 

---

예제 5) 유리수 집합 $\mathbb{Q}$ 는 가부번집합인가?

 

Sol) $\mathbb{Z}$ 는 가산집합이고, 따름정리 $(S.T)$ 4.10.1) 에 의해 $\mathbb{Z}-\left\{ 0 \right\}$ 또한 가산집합이다. 그러면 따름정리($S.T$) 4.12) 에 의해

 

$$\mathbb{Z}\times \left( \mathbb{Z}-\left\{ 0 \right\} \right)=\left\{ (a,b)\mid a,b\in\mathbb{Z}\;,\;b\neq 0 \right\}$$

 

또한 가산집합이다. 그러면 함수 $f:\mathbb{Z} \times \left( \ \mathbb{Z}-\left\{ 0 \right\} \right)\rightarrow \mathbb{Q}$ 를 $f(a,b):=\displaystyle\frac{a}{b}$ 로 정의하면 따름정리 ($S.T$) 4.12.1) 에 의하여 $f\left( \mathbb{Z}\times \left( \mathbb{Z}-\left\{ 0 \right\} \right) \right)$ 또한 가부번집합이다. 그런데 $f\left( \mathbb{Z}\times \left( \mathbb{Z}-\left\{ 0 \right\} \right) \right)=\mathbb{Q}$ 이므로^[각주:1] $\mathbb{Q}$ 또한 가부번집합이고, $\mathbb{N}\subset\mathbb{Q}$ 이다. 즉 $\mathbb{Q}$ 는 유한집합이 아닌 무한집합이므로 가산집합이다. $_\blacksquare$

 

 

정리($S.T$) 4.15)
모든 무한집합은 가부번인 부분집합을 가진다. 즉 임의의 무한집합 $X$ 에 대해 $Y\subseteq X$ 인 가부번집합 $Y$ 가 존재한다.

증명) $X$ 가 무한집합이라고 가정하자.

$X\neq \phi$ 이므로, 어떤 하나의 원소 $x_1\in X$ 를 고를 수 있다. $X$ 가 무한집합이므로, $X-\left\{ x_1 \right\}\neq \phi$ 이고 $x_2\in X-\left\{ x_1 \right\}$ 를 다시 고를 수 있다. 이렇게 $k-1$ 을 반복하여 $x_1,\cdots x_{k-1} \in X$ 라 해보자. 그러면 $X$ 는 무한집합이므로 여전히 $X-\left\{ x_1,\cdots x_{k-1} \right\}\neq \phi$ 가 성립하고, $x_k\in X-\left\{ x_1,\cdots x_{k-1} \right\}$ 를 고를 수 있다. 그러면 $\left\{ x_k\mid k\in \mathbb{N} \right\}=\left\{ x_1,x_2,\cdots, \right\}\sim \mathbb{N}$ 이고 $\left\{ x_k\mid k\in \mathbb{N} \right\}:=Y\subseteq X$ 이므로 $Y$ 는 가부번집합이다. $_\blacksquare$

 

 

이 정리가 의미하는 바는 사실 가부번집합이 모든 무한집합들이 공유하는 부분집합 중 가장 작은 사이즈의 부분집합이라는 것입니다. 왜냐하면, 말그대로 그 어떤 무한집합들도, 반드시 가부번집합을 가지고 있다는 것이기 때문입니다. 이와 연관된 다음 예제를 하나 풀어봅시다. 이 예제는 '기수(cardinal number)'를 알고 있어야 해서 정확히는 다음 글들을 확인하고 오시는 것이 편합니다.

---

예제 6) $a$ 를 임의의 초한기수(transfinite cardinal number)라 하자. 그러면 $\left| \mathbb{N} \right| \leq a$ 임을 보여라. 즉, $\left| \mathbb{N} \right|$ 가 가장 작은 초한기수라는 뜻이다.

 

sol) 귀류법을 사용하기 위해 $a < \aleph_0 = \left| \mathbb{N} \right|$ 라 가정하자. 그리고 $\left| A \right|=a$ 라 하자. 위의 정리($S.T$) 4.15) 에 의하여 $A$ 는 무한집합이므로 $B\subseteq A$ 인 가부번인 부분집합 $B$ 가 반드시 존재한다. 그러면 $B\sim \mathbb{N}$ 이므로 $\left|  B \right|=\aleph_0$ 이다.

 

그런데 $B\subseteq A$ 이므로, 이때 $f:B\rightarrow A$ 인 단사함수를 잡을 수 있고^[각주:2] 따라서 $B\sim f(B)$ 이다. 그러면 따름정리($S.T$) 4.17.2) 에 의하여 $B$ 의 기수는 $A$ 보다 작거나 같아야 한다. 그러면 $\aleph_0=\left|B \right|\leq \left|A \right|=a$ 가 되고 이는 $a < \aleph_0$ 이라는 가정에 모순이다. 따라서 주어진 명제는 참이다. $_\blacksquare$

 

 

 

[참고문헌]

You-Feng Lin, Shwu-Yeng T,Lin - Set thoery

 

 

 

 

1. 왜냐면 이게 유리수의 정의이기 때문 [본문으로]
2. 단사함수를 잡을 수 있는 이유는? 애초에 무한집합의 정의가 그렇지요. [본문으로]