반응형
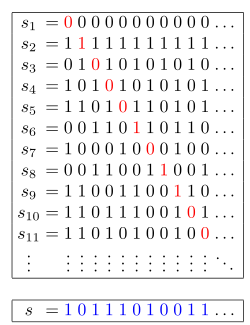
칸토어의 대각법은 수학에서 몇가지 중요한 정리들을 증명하는데 사용됩니다. 매우 참신한 아이디어라 이를 어떻게 떠올렸을지 참 신기한 생각이 많이 듭니다. 오늘은 칸토어의 대각법을 이용해서 실수 집합이 무한집합이며 가부번집합이 아님을 증명할 것입니다. 결과를 먼저 설명하면 여태까지 자연수, 정수, 유리수가 가부번집합임을 보였는데, 실수는 비가부번 즉 비가산집합이고, 무리수 집합 역시 그러합니다.
공교롭게도 이 수학 개념이 2024년 수능특강 독서의 과학/기술 2번째 지문으로 수록되어 있습니다. 수학적으로 증명을 하는 과정은 고등학생에게 대단한 도전이 될 수 있습니다. 그럼에도 제가 고등학생 수준으로 약간 눈높이를 낮추어 영상을 만든 것이 있습니다. 이곳을 참고하시기 바랍니다.
1. 실수는 비가산집합이다.
정리($S.T$) 4.16)
실수 $\mathbb{R}$ 의 부분집합 $(0,1)$ 은 무한집합이고, 비가부번집합(따라서 비가산집합)이다.
증명) $x\in (0,1)$ 에 속하는 모든 수 $x$ 를 $x=0.x_1x_2x_3\cdots$ 의 형태로 전개한다. 여기서 각각의 $n\in\mathbb{N}$ 에 대하여 $x_n\in \left\{ 0,1,2,\cdots ,9 \right\}$ 가 된다.
그런데 유한소수나 순환소수는 분수 표현로 나타낼 수 있는데, 유한소수로 표현되는 숫자도 무한소수로 표현하려고 한다. 이때 $0.999... =1 $을 이용한다. 예를 들면 $0.5=0.4999.....$ 라 표기하는 것이다.
그러면 임의의 $x,y\in (0,1)$ 에 대하여 $x=0.x_1x_2x_3\cdots \;,\; y=0.y_1y_2y_3\cdots$ 로 표현할 때, 모든 첨자 $k\in\mathbb{N}$ 에 대하여 $x_k=y_k$ 이어야만 두 수가 같다. 고로 임의의 소수점 아래 $k$ 번째 자리에서 $x_k\neq y_k$ 가 성립하면(단 하나의 $k$ 에 대해서 성립하기만 해도) 두 수는 같지 않아, $x\neq y$ 인 셈이다.
이를 바탕으로 주어진 명제를 증명하자. 귀류법을 사용하기 위해 $(0,1)$ 이 가부번집합이라 가정해보자. 그러면 일대일대응인 함수 $f:\mathbb{N}\sim (0,1)$ 이 존재하여 $(0,1)$ 의 원소를 다음과 같이 나열한다고 생각해보자.
$$\begin{align*}
f(1)&=0.a_{11}a_{12}a_{13}\cdots \\
f(2)&=0.a_{21}a_{22}a_{23}\cdots \\
f(3)&=0.a_{31}a_{32}a_{33}\cdots \\
&\;\;\;\;\;\;\;\vdots \\
f(k)&=0.a_{k1}a_{k2}a_{k3}\cdots \\
\end{align*}$$
이때 각 $a_{ij}$ 에 대하여 $a_{ij}\in \left\{ 0,1,2,\cdots ,9 \right\}$ 이 성립한다. 이제 위에 나열된 모든 $f(k)$ 들 중에 어느 것과도 일치하지 않는 수 $z\in (0,1)$ 가 존재함을 통해 모순을 일으키려고 한다. $z=0.z_1z_2z_3\cdots $ 의 각 $z_k$ 를 다음과 같이 정의하자.
$$z_k= \left\{ \begin{array}{cl}
5 & (a_{kk}\neq 5) \\
1 & (a_{kk}=5)
\end{array} \right.$$
이렇게 $z_k$ 를 정의하면,1 모든 $k\in\mathbb{N}$ 에 대해 $z_k\neq a_{kk}$ 가 된다. 왜냐하면 위의 정의에 따라 $a_{kk}$ 와 항상 같지 않게 $z_k$ 를 정의하기 때문이다. 따라서 $z\neq f(1)$, $z\neq f(2)$, $z\neq f(3)$, $\cdots \;\; z\neq f(k)$ 가 되면서 $z\notin f(\mathbb{N})=(0,1)$ 이 성립한다. 고로 이것은 $z\in (0,1)$ 에 대해 모순이므로 주어진 명제는 참이다. $_\blacksquare$
이 증명법을 칸토어의 대각법이라고 부릅니다. 각각의 $f(k)$ 에 존재하는 $a_{kk}$ 소숫점의 숫자들과 다른 숫자들로 $z$ 를 구성하여 모순을 이끌어내기 때문입니다.
따름정리($S.T$) 4.16.1)
실수 집합 $\mathbb{R}$ 은 무한집합이고, 비가부번집합, 곧 비가산집합이다.
따름정리($S.T$) 4.16.2)
무리수 집합도 무한집합이고, 비가부번집합, 곧 비가산집합이다.
첫 번째 따름정리의 증명) 예제 1)과 예제 2), 그리고 동치관계의 추이성을 고려하면 $(0,1)\sim \mathbb{R}$ 이다. 따라서 $\mathbb{R}$ 은 비가산집합이다. $_\blacksquare$
두 번째 따름정리의 증명) 무리수 집합은 $\mathbb{R}-\mathbb{Q}$ 으로 나타낼 수 있다. 이것이 가부번집합이라고 가정하자. $\mathbb{Q}$ 은 가부번집합이므로, 정리($S.T$) 4.11) 에 의하여 합집합 $(\mathbb{R}-\mathbb{Q})\cup \mathbb{Q} = \mathbb{R}$ 또한 가부번집합이다. 이는 $\mathbb{R}$ 이 비가산집합이므로 모순이다. 따라서 주어진 명제는 참이다. $_\blacksquare$
[참고문헌]
You-Feng Lin, Shwu-Yeng T,Lin - Set thoery
- 그래서 이 정의에서 5나 1이라는 숫자가 굳이 중요한 것은 아닙니다. 그냥 임의의 두 수를 선택하면 됩니다. [본문으로]
'집합론(Set Theory) > 기수론' 카테고리의 다른 글
| 기수의 덧셈과 곱셈(Addition and product of cardinal number) (2) | 2023.11.27 |
|---|---|
| 칸토어의 정리(Cantor's Theorem) (0) | 2023.11.26 |
| 집합의 기수와 칸토어-슈뢰더-베른슈타인 정리(Cardinal number of set and Cantor-Schröder-Bernstein Theorem) (1) | 2023.11.26 |
| 가부번집합과 가산집합(Denumerable and countable set) (1) | 2023.11.25 |
| 유한집합과 무한집합(Finite and Infinite sets) (1) | 2023.11.16 |




댓글