대학교에서 수학은 공과대학, 수학과, 물리학과, 경제학과 등 수많은 학과에서 사용합니다. 그 중 너나할거 없이 배우는 알파이자 오메가인 과목이 미적분학이며, 이 다음으로 중요한 것이 바로 선형대수학입니다. 그런데 미적분학과 달리 선형대수학은 고등학교에서 볼 수 없었던 엄밀한 논리와 추상적인 전개로 점철되어 있으며 대학 수학의 기초이자 진수를 보여줍니다. 그렇지만, 수학과를 제외한 타 학과에서는 선형대수학을 배우긴 하지만 아무래도 아주 자세하게 배우진 않고, 응용할 수 있는 도구들 중심으로 배우게 됩니다. 예컨대 행렬식, 행렬연산, 행렬의 대각화, 고유값 문제, 선형독립/종속, 선형결합, 선형변환 등이 그 대상입니다.
하지만, 선형대수학의 출발은 벡터와 스칼라가 무엇인지 규정하는 일에서 시작하여 벡터공간이 무엇인지를 공리 8가지로 정의하고 여러 논리를 펼쳐나가는 것이 가장 정석적인 경로입니다. 미적분학이나 고등학교 과정까지의 수학에서 우리가 알고 있는 벡터는 역학에서 많이 봤을 법한 기하학적 의미로 정의한 것으로, 바로 '크기와 방향을 가진 물리량'에 해당하는 대상입니다. 그런데, 선형대수학에서 벡터는 벡터공간의 공리를 만족시키면 그 어떤 대상도 벡터가 될 수 있습니다. 이처럼 공업수학이나 수리물리학책에는 선형대수학의 기본적 내용이 잘 나와있지 않은 경우가 많은데, 공학이나 물리를 다루는 입장에서 최대한 알아야 하는 것을 위주로 포스팅을 해보려고 합니다.
벡터공간에 대한 개념을 이해하기 위해서는 대수학에서 군, 환, 체가 무엇인지 이해할 필요가 있습니다. 대수학에서야 군, 환, 체의 뼈대를 세우는 일이 매우 중대한 일이지만, 개념 자체는 어렵지 않기도 하고 이 포스팅에서는 간단히 짚고 나서 선형대수학을 시작해 보도록 하겠습니다.
1. 이항 연산(Binary operation)
먼저 '연산(operation)'이 무엇인지 정의하고 넘어가야 합니다. 우리가 초등학생 때부터 알고 있는 연산은 사칙연산이 있는데, 이외에도 적분을 하는 것도 연산의 일종이고, 단지 어떤 대상과 대상을 연결시켜 조합을 만들어내는 행위를 연산의 일종이라고 볼 수 있습니다. 이것의 정의는 다음과 같습니다.
정의($A.A$) 0-1) 이항연산
집합 $X\left ( \neq \emptyset \right )$가 '$*$'을 '이항연산(Binary operation)' 또는 '연산(operation)'으로 갖는다는 것은 $\forall \,a,b\in X$ 에 대해 $a*b\in X$ 일 때를 말한다. 그리고 이 때 $X$는 연산 $*$ 에 대해 '닫혀 있다(closed)'고 한다.
쉽게 말하자면 어떤 집합의 두 원소를 뽑아내서 둘을 연산시켰을 때, 그 연산의 결과물도 집합 X 내에 포함된다면 이 연산이 집합에 대해 닫혀 있다(closed)고 말할 수 있다는 것입니다.
예를 들어 자연수는 덧셈과 곱셈에 대해 닫혀 있습니다. 임의의 자연수를 뽑아 덧셈이나 곱셈을 해도, 여러번 할지라도, 여전히 자연수이기 때문입니다. 반면 뺄셈1에 대해서는 닫혀 있지 않습니다. $3-5=-2$ 는 자연수가 아니고, $5-5=0$ 도 자연수가 아니죠. 이러한 예시들이 많습니다.
위 개념은 정의를 기억하고 나서 자연수, 정수, 유리수, 무리수, 실수에 대해 사칙연산의 닫혀 있는지에 대한 여부 정도만 확인하고 넘어가도 충분합니다.

2. 군(群, Group)
군, 환, 체 중 연산의 기초 중 기초적인 성질이 성립하는 집합을 가리키는 것이 군으로, 정의는 아래와 같이 합니다.
정의($A.A$) 0-2) 군(group)
$*$ 을 연산으로 갖는 집합 $G\left ( \neq \emptyset \right )$ 가 임의의 $\forall \,a,b,c\in G$ 에 대하여
① 결합법칙(Associative) : $(a*b)*c=a*\left ( b*c \right )$
② 항등원(Identity)의 존재 : $e\in G$ 가 존재하여 $a*e=e*a=a$
③ 역원(Inverse)의 존재 : $a^{-1}\in G$ 가 존재하여 $a*a^{-1}=a^{-1}*a=e$
을 만족하면 $G$는 '군(Group)'이라 한다. $G$가 연산 $*$ 를 갖는 군이면 보통 $(G,*)$ 로 표기한다. 덧붙여 만약 $\forall \, a,b\in G$에 대하여
④ 교환법칙(Commutative) : $a*b=b*a$ 를 만족하면 $G$는 '아벨군(Abelian Group)' 또는 '가환군(Commutative group)' 이라 부른다.
항등원이란 연산해서 자기 자신을 만드는 어떤 집합의 원소라 볼 수 있습니다. 함수에서 항등원의 개념은 항등함수이고, 행렬에서는 항등행렬입니다. 임의의 행렬에 항등행렬을 무한히 곱해도 여전히 원래 행렬 그대로의 형태가 남기 때문이죠. 역원은, 항등원의 결과가 나오게 하는 원소로 함수에서 역함수, 행렬에서 역행렬의 지위를 맡고 있는 친구입니다.
3. 환(環, Ring)
정의($A.A$) 0-3) 환(Ring)
합과 곱을 연산으로 갖는 집합 $R\left ( \neq \emptyset \right )$ 에 대해 $R$이 덧셈 아벨군이라 하자. $\forall \,a,b,c\in R$ 에 대하여
① 곱셈에 대한 결합법칙(Associative) : $a(bc)=(ab)c$
② 분배법칙(Distribute) : $a(b+c)=ab+ac\,,\,(a+b)c=ac+bc$
③ 또 $\forall\, a\in R$ 에 대하여 곱셈에 대한 항등원 $1a=a1=a$ 인 $1\in R$ 이 존재
을 만족하면 $R$을 '단위원을 갖는 환(Ring with unity)'이라 한다.2
덧붙여 $\forall\,a,b\in R$ 에 대하여
④ 곱셈에 대한 교환법칙(Commutative) : $ab=ba$
가 성립하면 $R$을 '가환환(Commutative Ring)' 이라 부른다.
환은 덧셈 아벨군의 조건을 만족하면서 곱셈에 대한 결합법칙, 분배법칙까지 성립하는 것이고 추가적으로 교환법칙이 성립하면 가환환이라 합니다. 정수 전체의 집합 Z와 유리수 전체의 집합 Q, 실수 전체의 집합 R, 복소수의 집합 C는 모두 가환환입니다. 곱셈과 덧셈에 대해 교환법칙까지 항상 성립하기 때문이죠.
선형대수학에서 매우 자주 등장하는 행렬은, 행렬의 곱셈의 경우 일반적으로 교환법칙이 성립하지 않는다는 사실 정도는 들어보셨을 것입니다. $M_n(R)$ - $n$차 정사각행렬, 성분이 환의 원소임을 뜻함 - 은 가환환이 아닌 환으로 간단히 비가환환이라고 합니다.
이렇게 군 > 환 > 체 순서로 어떤 집합의 범위를 좁혀나가는 것은 연산을 얼만큼 자유자재로 할 수 있는지 적당한 집합을 찾는 것이 목적이기 때문입니다. 대수학에서는 사칙연산을 할 수 있는 대상을 찾는 것에 관심이 있기 때문입니다. 그래서 가장 간단한 덧셈부터 시작해서 가장 복잡한 나눗셈까지 기본적인 연산법칙들이 성립하는 집합을 찾아가는 것이 목적이라 할 수 있습니다.
4. 체(Field)
체는 가장 중요하고 빈번히 등장하는 연산이 잘 정의되는 집합입니다. 누구나 하는 말이지만, 체는 사칙연산(나눗셈까지)이 모두 별다른 문제없이 잘 수행할 수 있는 대상을 모은 집합이라 볼 수 있습니다.
체를 정의하기 전에 곱셈에 대한 역원을 정의해야 합니다. R에서 하나 임의로 뽑은 원소에 대해 곱해서 항등원이 되게 하는 원소가 존재할 때, 뽑은 원소를 가역원, 곱해져서 항등원을 만드는 원소를 역원이라 합니다. 이는 조금만 자세히 들여다보면 결국 나눗셈을 하겠다는 의도가 깔려있는 것으로 파악할 수 있습니다.
정의($A.A$) 0-4)
$R$이 단위원을 갖는 환 일 때 $a\in R$ 에 대하여 곱셈에 대한 역원 $ab=1=ba$인 $b\in R$ 이 존재하면, $a$를 '가역원(Invertible element)'라고 한다. 또한 $b$는 $a$의 곱에 대한 '역원(Multiplication inverse)'라 한다.
체의 정의는 다음과 같습니다.
정의($A.A$) 0-5) 체(Field)
집합 $F$가 단위원을 갖는 가환환이라 하자. 만약 $F^*=F-\left \{0 \right \}$ 의 모든 원소가 가역원이면, 즉 $\forall\,a\in F$가 곱에 대한 역원을 갖는다면 $F$를 '체(Field)'라 한다.
이는 곧, 덧셈($+$)과 곱셈($\times\;\mathrm{or}\;\cdot$)에 대한 교환법칙, 결합법칙, 분배법칙이 성립하고 항등원과 역원이 각각 존재하는 집합을 '체(Field)'라 한다는 것과 같다.
유리수 집합 $\mathbb{Q}$, 실수 집합 $\mathbb{R}$, 복소수 집합 $\mathbb{C}$는 모두 체입니다. [표 1]을 참고하면 좋을 듯 합니다. 반면 나눗셈과 정수는 체의 조건을 만족시키지 못하지요. 체가 되는 집합은 셀 수 없이 많은데, 몇가지만 다루어 보도록 합시다.
예제 1) 2로 나누었을 때 나머지를 모은 집합 $\mathbb{Z}_2$가 Field 인지 검증하여라.
2로 나눈 나머지는 0,1 뿐이므로 $\mathbb{Z}_2$ 의 원소는 이 두개입니다. 그럼 0과 1에 대해 각각 체의 정의를 만족하는지 확인해보면 됩니다. 일단 덧셈과 곱셈을 해봅시다.
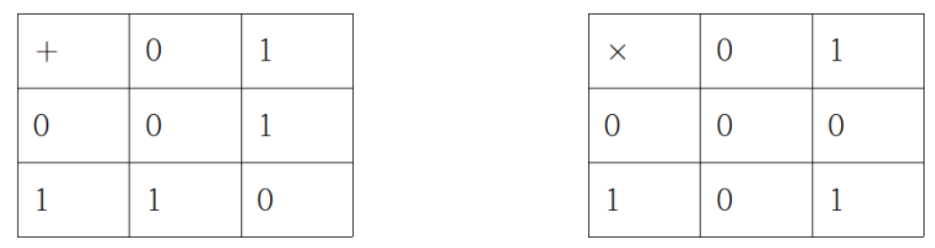
여기서 왜 $1+1$이 $2$가 아니라 $0$이 되는지 궁금증이 생길 수 있습니다. $\mathbb{Z}_2$에서 덧셈을 한다는 것은 단순히 더한다는 것이 아니라 더한 숫자를 다시 $2$로 나누었을 때 나머지가 무엇인지를 확인하는 행위입니다. $1+1=2$를 다시 $2$로 나누면 나머지가 $0$이니, $Z2$에서 $1+1$은 $0$입니다. 같은 원리로 $1+0=1$을 다시 $2$로 나누면 나머지가 1입니다. 곱셈 역시 마찬가지로 하면 됩니다. 그러면 [표 2] 에서 확인할 수 있듯이 반드시 연산 결과가 0 또는 1만 나오게 되지요. 이 표를 통해 체의 조건을 모두 만족함을 알 수 있습니다. 예를 들어, 1의 덧셈에 대한 항등원은 $1+e=e+1=1$ 을 만족하는 $e=0$ 이고, 역원은 $1+i=i+1=0$ 을 만족하는 $i=1$ 인 것입니다.
예제 2) 다음 집합이 체(field)임을 보여라.
$$\mathbb{Q}\left [ \sqrt 2 \right ]=\left \{ a+b\sqrt 2 \mid a,b\in \mathbb{Q} \right \}$$
곱셈에 대한 교환법칙 : $\left ( a+b\sqrt 2 \right )\left ( c+d\sqrt 2 \right )=\left ( c+d\sqrt 2 \right )\left ( a+b\sqrt 2 \right )$ 가 성립하니 가환환
곱셈에 대한 항등원 : $\left ( a+b\sqrt 2 \right )\times 1=\left ( a+b\sqrt 2 \right ) 에서 1=1+0\sqrt 2\in \mathbb{Q}$ 이므로 존재
덧셈에 대한 교환법칙 : $\left ( a+b\sqrt 2 \right )+\left ( c+d\sqrt 2 \right )=\left ( c+d\sqrt 2 \right )+\left ( a+b\sqrt 2 \right )$ 성립
덧셈에 대한 항등원 : $\left ( a+b\sqrt 2 \right )+0=\left ( a+b\sqrt 2 \right )$ 존재
덧셈에 대한 역원 : $\left ( a+b\sqrt 2 \right )+\left ( -a-b\sqrt 2 \right )=0 에서 -a-b\sqrt 2\in \mathbb{Q}$ 이므로 존재
곱셈에 대한 역원이 존재할까요? 역원은 여기서 역수에 해당하는데,
$$\left ( a+b\sqrt 2 \right )^{-1}=\frac{1}{\left ( a+b\sqrt 2 \right )}
=\frac{a-b\sqrt 2 }{a^2-b^2\sqrt 2^2}=\frac{a}{a^2-2b^2}-\frac{b}{a^2-2b^2}\sqrt 2 \in \mathbb{Q}$$
을 계산해보면 존재함을 알 수 있습니다. 그러니 주어진 집합은 Field 입니다.
[참고 문헌]
선형대수학, 청문각, 강경태·송석준 지음
'대수학(Abstract Algebra) > 순열, 치환' 카테고리의 다른 글
| 부호함수와 치환(Signum function with Permutation) (0) | 2020.12.08 |
|---|---|
| 대수학에서 호환과 짝치환, 홀치환 (Transposition and even, odd permutation in Algebra) (2) | 2020.12.08 |
| 대수학에서 순환의 서로소의 뜻과 교환법칙(Commutative laws in Mutually disjoint of Cycle) (0) | 2020.12.06 |
| 대칭군(The symmetric group) (0) | 2020.12.06 |
| 대수학에서 치환과 순환(Permutation and cycle in Algebra) (2) | 2020.12.03 |




댓글