전류의 정의(Electric currents)

전류는 중학 과학에서 등장하지만, 자기장을 이해하는 핵심 열쇠입니다. 이후부터 등장하는 전자기학에서 전류는 거의 빠지지 않고 항상 등장합니다. 전류의 중요성은 정전기학에서 전하가 하던 역할을 정자기학에서는 전류가 하게 된다는 사실에서 어렵지 않게 알 수 있습니다. 도입부에서 전기장은 전하에 의해 생성되고, 자기장은 전류에 의해 생성됨을 역설했었습니다.

 

물론, 전자기학을 좀 더 깊게 파보면 전류가 자기장을 만드는 것은 맞지만 전류보다 더 심층적인 자기장의 근원을 탐구하면 자기장의 발산이 0이라는 점으로부터, 근원이 없음을 알 수 있습니다. 즉 자하(magnetic charge)는 아직 전하와 달리 인류가 발견하지 못했고, 맥스웰 법칙의 두번째 식은 아직 깨지지 않았습니다. 이 내용까지 달려가기 위해선 정자기학을 열심히 정리해야 합니다.

---

1. 전류(Electric current)

 

1) 정의

 

단위 시간동안, 도선의 어느 한 지점을 지나가는 전하량을 '전류(Electric current or current)'라 정의한다. 단위는 1초당 1C(쿨롱)을 뜻하는 '암페어(Ampere)'로 나타낸다.
$$I:=\frac{dq}{dt} \;\;\;,\;\;\; 1[\mathrm{A}]=1[\mathrm{C/s}]\;\;\;\;\;\cdots \;\;\;(1)$$ $$\mathbf{I}=\lambda \mathbf{v}$$

 

기호 $:=$ 는 왼쪽에 있는 물리량을 오른쪽에 있는 것과 같이 정의한다는 뜻입니다. 보통 이 기호는 수학에서 많이 쓰고, 물리에서는 대신 $\equiv$ 을 많이 쓰지만 이제부터는 수학의 기호를 사용하려 합니다.

 

전류의 정확한 정의는 위와 같이 초당 지나가는 전하량이니 분자와 분모에 $d$를 붙여야 하지만, 그 값이 일정한 경우에는 다들 알다 시피 $I=\displaystyle\frac{Q}{t}$ 라고 써도 무방합니다. 많은 경우에는 이것이 가능한데, 세밀한 계산을 하거나 값이 바뀔 때는 정확한 정의 식을 이용하면 됩니다.

 

 

2) 도선에 흐르는 전류로 구한 자기력

 

 

[그림 1]

 

선밀도가 $\lambda$ 인 전하가 도선을 따라 속력 $v$로 달린다고 하면, 시간 $dt$ 동안 [그림 1]에서와 같이 점 $P$를 지나는 전하의 양은, 길이가 $v\,dt$ 인 도선토막 안에 들어있는 전하량 $\lambda v\,dt$ 와 같게 됩니다. 그러면 여기서 전류를 다시 쓸 경우

 

$$I=\frac{dq}{dt}=\frac{dq}{dl}\frac{dl}{dt}=\lambda v$$

 

 가 됩니다. 여기서 속력은 속도 벡터로 바꿔 방향을 나타낼 수 있고, 전류도 흐름이기 때문에 벡터량으로 나타낼 수 있습니다.

 

$$\mathbf{I}=\lambda \mathbf{v}\;\;\;\;\;\cdots \;\;\;(2)$$

 

 

3) 자기력 새로 쓰기

 

로런츠 힘에서 자기력을 쓸 때 식 $(2)$를 이용해 봅시다.

 

$$F_m=\int \left( \mathbf{v}\times \mathbf{B} \right)\,dq= \int \left( \mathbf{v}\times
\mathbf{B} \right)\,\lambda\, dl=\int \left( \mathbf{I}\times \mathbf{B} \right)\,dl$$

 

여기서 전류와 미소 변위 벡터 $d\mathbf{l}$ 의 방향은 같고, 전류의 크기가 일정하다고 생각하면 식을 다음과 같이 바꿀 수 있습니다.

 

정리($E.M$) 4.6

자기력은 다음과 같이 새로 쓸 수 있다.
$$\mathbf{F}_m=q(\mathbf{v}\times \mathbf{B})=I\int\left( d\mathbf{l}\times \mathbf{B} \right)\;\;\;\;\;\cdots \;\;\;(3)$$

 

식 (3)은 자주 쓰일기 때문에 기억해야 합니다.

---

2. 면전류(Surface current)

 

1에서의 전류는 도선에 흐르는 전하의 흐름을 말하지만, 전류가 면이나 부피에서 흐르는 2차원과 3차원의 상황을 고려하는 것이 자연스럽습니다. 실제 우리가 보는 도선은 엄밀하게는 3차원의 것이기 때문에, 전자기학에서는 전류만큼 전류밀도를 많이 고려하게 됩니다. 차원을 하나씩 확장해 봅시다.

 

1) 정의

 

단위 길이의 폭을 표면에서 지나가는 전류는 '표면전류밀도(Surface current density)'로 기술하고 $K$로 나타낸다.
$$\mathbf{K}=\frac{d\mathbf{I}}{dl_\bot }=\sigma \mathbf{v}\;\;\;\Leftrightarrow \;\;\;
\mathbf{I}=\int \mathbf{K}\cdot d\mathbf{l}_\bot\;\;\;\;\;\cdots \;\;\;(4)$$

 

두번째 식은 유도가 필요합니다.

증명) 폭을 $dl_\bot$, 길이를 $dl_{\parallel}$ 이라 하자. 면전하 밀도는 $\sigma=\displaystyle\frac{dq}{dA}$ 이고 속도는 $v=\displaystyle\frac{dl_\parallel}{dt}$ 이므로,
$$\begin{align*}
\sigma \mathbf{v}&=\frac{dq}{dA}\frac{dl_\parallel}{dt}=\frac{dq}{dl_\bot d_\parallel}\frac{dl_\parallel}{dt}
\\\\&=\frac{dq}{dt}\frac{1}{dl_\bot}=\frac{d\mathbf{I}}{dl_\bot }=\mathbf{K}
\end{align*}$$

 

[그림 2] 면전류

 

표면전류를 도입하면 자기력 식도 다음과 같이 바꿀 수 있습니다.

 

정리($E.M$) 4.7

표면전류밀도 $\mathbf{K}$ 를 이용해서 자기력을 나타내면,
$$\mathbf{F}_m=\int \left( \mathbf{v}\times \mathbf{B} \right)\,\sigma\,da=\int \left( \mathbf{K}
\times \mathbf{B} \right)\,da\;\;\;\;\;\cdots \;\;\;(5)$$

 

---

3. 부피전류(Volume current)

 

1) 정의

 

3차원 공간을 흐르는 전류는 단위면적을 지나는 전류인 '부피전하밀도(Volume current density)' 로 정의되는 양을 도입해서 표현하고, $\mathbf{J}$ 로 표기한다.
$$\mathbf{J}=\frac{d\mathbf{I}}{da_\bot }=\rho \mathbf{v}\;\;\;\Leftrightarrow \;\;\;
\mathbf{I}=\int \mathbf{J}\cdot d\mathbf{a}_\bot\;\;\;\;\;\cdots \;\;\;(6)$$

 

역시 두번째 식을 유도해 봅시다.

 

증명) $\rho=\displaystyle\frac{dq}{dV}\;\;,\;\;v=\displaystyle\frac{dl_\parallel}{dt}$ 이므로
$$\begin{align*}
\rho \mathbf{v}&=\frac{dq}{dV}\frac{dl_\parallel}{dt}=\frac{dq}{da_\bot d_\parallel}\frac{dl_\parallel}{dt}
\\\\&=\frac{dq}{dt}\frac{1}{da_\bot}=\frac{d\mathbf{I}}{da_\bot }=\mathbf{J}
\end{align*}$$

 

[그림 3] 부피전류

 

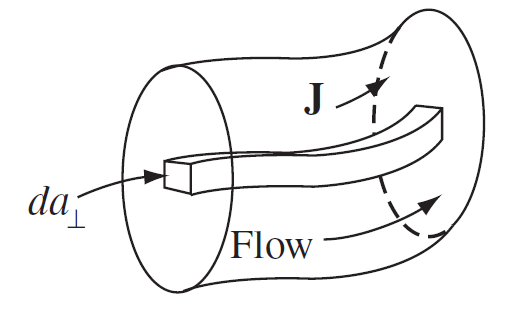
부피전류를 도입하여 자기력을 또 한번 고쳐 쓸 수 있습니다. 사실 3차원에서의 식이 가장 일반적이기 때문에, 시간이 지날 수록 새로 쓴 자기력 공식 중 이 식을 가장 많이 쓰게 될 것입니다.

 

정리($E.M$) 4.8

부피전류밀도 $\mathbf{J}$ 를 이용해서 자기력을 나타내면,
$$\mathbf{F}_m=\int \left( \mathbf{v}\times \mathbf{B} \right)\,\rho\,d\tau=\int \left( \mathbf{J}
\times \mathbf{B} \right)\,d\tau\;\;\;\;\;\cdots \;\;\;(7)$$

 

 

 

4. 연속 방정식

 

전자기학에서 연속 방정식을 정상정류에 대해서 정리할 수 있습니다. 식 $(6)$ 에 의하면, 면 $\mathcal{S}$ 를 지나는 총 전류는 면 전체에 대해 적분하면 됩니다.

 

$$I=\int_{\mathcal{S}}^{}d\mathbf{I}=\int_{\mathcal{S}}^{}\mathbf{J}\cdot d\mathbf{a}=\int_{\mathcal{S}}^{}J\,da_{\perp}$$

 

그러면 단위시간당 부피 $\mathcal{V}$ 를 빠져나가는 총 전하량은,

 

$$\oint_{\mathcal{V}}\mathbf{J}\cdot d\mathbf{a}=\int_{\mathcal{V}}^{}\left( \nabla\cdot\mathbf{J} \right)d\tau$$

 

가 되는데, 전하는 없어지거나 스스로 생기지 않으므로 보존됩니다. 고로 표면을 지나 밖으로 나가는 양만큼 반드시 속에 있던 전하가 줄어들어야 합니다. 이를 식으로 연결하면, 전류밀도의 발산을 부피적분한 것이 총 전하량의 시간당 감소율임을 알 수 있습니다.

 

$$\int_{\mathcal{V}}^{}\left( \nabla\cdot\mathbf{J} \right)d\tau =-\frac{d }{dt}\int_{\mathcal{V}}^{}q\,d\tau
=-\int_{\mathcal{V}}^{}\left( \frac{\partial \rho}{\partial t} \right)d\tau$$

 

이것은 어떤 부피 $\mathcal{V}$ 에 대해서 성립하기 때문에, 다음과 같이 정리합니다.

 

정리($E.M$) 4.9
[연속방정식(Continuity equation)]
임의의 부피 $\mathcal{V}$ 에 대하여 다음이 성립한다. 이는 국소영역에서 전하의 보존을 나타내는 식이다.
$$\int_{\mathcal{V}}^{}\left( \nabla\cdot\mathbf{J} \right)d\tau =-\int_{\mathcal{V}}^{}\left( \frac{\partial \rho}{\partial t} \right)d\tau $$ $$\nabla\cdot\mathbf{J}+\frac{\partial \rho}{\partial t}=0$$

 

 

 

[참고문헌]

Introduction to Electrodynamics, Griffiths, 4e