흑체복사에서 발견된 문제점을 설명할 차례인데, 처음 타자는 빈의 변위 법칙입니다.
1. 빈의 변위 법칙
1) 유도

빈의 변위 법칙은 고등학교 과학에서도 나오고 파장에 대한 물리적 해석을 할 때 어느 정도 상식적으로 알고 있는 경우가 있는데, 양자역학에서 유도를 한 번 해봅시다. 참고로 이 유도 과정은 Gasiorowicz 교과서 첫 장 연습문제 1번에 수록되어 있습니다.
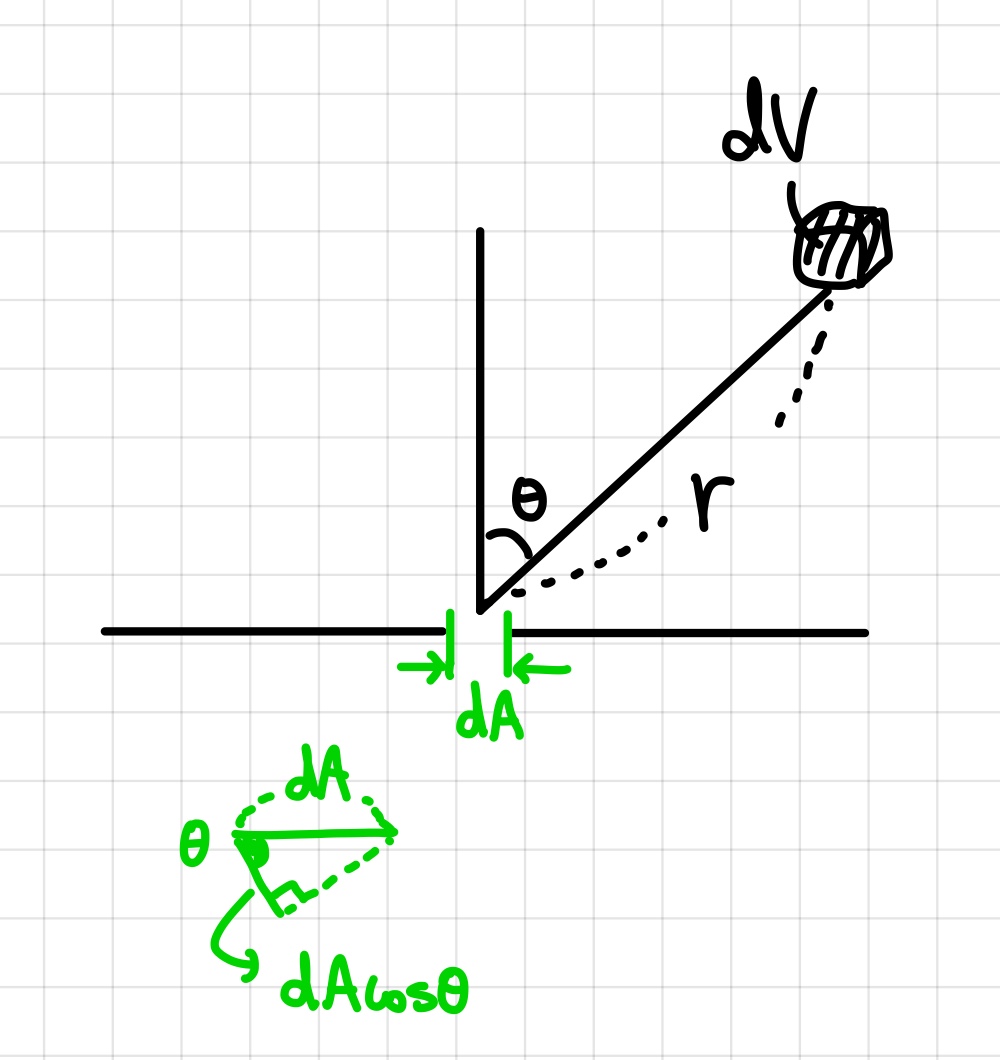
[그림 2]와 같이 틈의 폭이 $dA$ 이고 그 틈 안에 각도 $\theta$ 만큼 회전된 곳에, 미소 부피 $dV$ (또는 $d\tau$ 라고 적음)가 있으며 틈에서 그곳까지의 거리를 $r$이라고 해봅시다. 흑체는 이 틈 안쪽 영역에 해당하며 그 중에서 미소 부피에 해당하는 부분에 대해서 계산을 하려고 합니다. 우리가 구하고자 하는 것은 흑체의 단위 시간당 단위 면적에서 방출되는 에너지에 관한 것입니다.
흑체에서 방출되는 복사에너지 밀도(Energy density of radiation)를 $u(\lambda, T)$ 라고 해봅시다. 그냥 복사에너지는 $\xi(\lambda, T)$ 로 적습니다. 미소 부피 요소에서 방출되는 복사에너지 밀도는 구면좌표계를 고려하면
$$u(\lambda,T)dV=u(\lambda,T)r^2\sin\theta drd\theta d\phi\;\;\;\;\;\cdots \;\;\;(1)$$
가 됩니다. 그리고 복사에너지가 방출되는 상태가 등방적(isotrophic)이라고 가정하면,1 미소 면적 $dA$를 통해 빠져 나오는 복사에너지가 어느 정도 되는지를 측정하려고 합니다. 이 양을 $d\xi(\lambda, T)$ 라고 할 것입니다. 이를 구하려면 다음의 비례식을 세웁니다.
$$u(\lambda, T)dV:4\pi r^2=d\xi(\lambda, T):dA\cos\theta\;\;\;\;\;\cdots \;\;\;(2)$$
왜 비례식이 이와 같이 복잡한 형태로 나오는지 처음부터 좌절할 수 있습니다. 좌변의 첫 항은 흑체에서 방출되는 복사에너지 밀도를 뜻하고, 그것이 모든 방향으로 등방성을 가지면서 방출되니 원래는 구의 겉면적 $4\pi r^2$ 에 대응된다고 볼 수 있습니다. 우변을 보면, 미소 면적에서 방출되는 복사에너지의 양이 첫 항에 대응되는 것이고, 우변의 둘째 항에선 $dA$가 아니라 $dA\cos\theta$ 인 까닭은 미소 부피 $dV$에서 구멍을 향해 직진하는 빛이 구멍 틈에 대해서 수직이 아니기 때문에,
틈 중에서 $dV$를 향하는 방향의 틈 길이만을 뽑아내야 하기 때문에 $\cos\theta$ 를 곱해준 것입니다. 이에 의해 계산을 해보면,
$$d\xi=\frac{udV}{4\pi r^2}dA\cos\theta=\frac{1}{4\pi}\left( u\sin\theta\cos\theta \right)drd\theta d\phi dA$$
$$\xi = \int d\xi = \frac{u}{4\pi}dA\int_{0}^{c\Delta t}dr\int_{0}^{2\pi}d\phi\int_{0}^{\frac{\pi}{2}}
\sin\theta \cos\theta d\theta= \frac{u(\lambda,T)}{4\pi}dA\cdot c\Delta t$$
방출되는 복사에너지를 $\xi$ 라고 하였고, 그러면 흑체에서 단위 시간동안 단위 면적에서 방출되는 에너지는
$$E=\frac{\xi}{dA\Delta t}=\frac{c}{4}u(\lambda,T)\;\;\;\;\;\cdots \;\;\;(3)$$
의 관계가 있습니다. $c$는 상수이니, 이 방출되는 에너지는 곧 흑체에서의 복사에너지 밀도에 비례상수 $\displaystyle\frac{c}{4}$ 만 곱하면 된다는 뜻이지요.
빈(Wien)은 자신의 실험 결과로부터 복사에너지 밀도가 파장과 온도의 어떤 함수 $g(\lambda, T)$와 파장의 5제곱의 역수 곱이 비례함을 제안했습니다.
$$u(\lambda,T)=\frac{1}{\lambda^5}g(\lambda,T) \;\;\;\mathrm{where}\;\;\;
g(\lambda,T)\sim e^{\displaystyle \frac{-\beta f}{T}}\;\;\;\;\;\cdots \;\;\;(4)$$
이를 확인하기 위해, 파장이 $\lambda$ 와 $\lambda+d\lambda$ 사이의 값을 가지는 에너지 밀도는 $u(\lambda,T)d\lambda$ 임을 이용해 봅시다. 그런데 진동수에 관한 식을 사용할 것이라서
$$\lambda=\frac{c}{f}\;\;\Rightarrow \;\; \left| \frac{d\lambda}{df} \right|=\frac{c}{f^2}\;\;\;\;\;\cdots \;\;\;(5)$$
의 관계식을 뽑아냅니다. $\lambda$를 $f$에 대해 미분한 것으로 분수함수의 미분을 한 것입니다. 그러면 $u(\lambda,T)d\lambda = u(f,T)df$ 이므로
$$u(f,T)=u(\lambda,T)\left| \frac{d\lambda}{df} \right|=\frac{c}{f^2}u(\lambda,T)\;\;\;\;\;\cdots \;\;\;(6)$$
를 얻습니다. 이제 $(6)$을 $(4)$에 대입하여 정리하면
$$u(f,T)=cf^3g(\lambda,T)=Cf^3e^{\displaystyle \frac{-\beta f}{T}} \;\;\;\mathrm{where}\;\;\;
cg(\lambda,T)=Ce^{\displaystyle \frac{-\beta f}{T}}\;\;\;\;\;\cdots \;\;\;(7)$$
가 됩니다. 주의할 것이 소문자(lower case) $c$는 광속이고 대문자 $C$는 상수입니다.
빈이 알아내려고 했던 것은 최대 에너지 $E$를 줄 때의 진동수입니다. 왜냐하면 $E$ 는 복사에너지 밀도와 비례했는데 복사에너지 밀도를 위에서 $(7)$과 같이 수정하고 보니까 변수가 진동수가 되었기 때문입니다. 물론 파장에 관한 식으로 정리해도 상관은 없겠지요. 아무튼 이를 알아내려면 미분을 해서 0이 되는 진동수 값을 찾으면 됩니다. 그 때 최대 진동수를 $f_M$ 이라고 표기하면,
$$\left[ \frac{du(f,T)}{df} \right]_{f_M}=3f^2Ce^{\displaystyle \frac{-\beta f}{T}}-\frac{\beta}{T}e^{\displaystyle \frac{-\beta f}{T}}Cf^3=0$$
$$\therefore \;\; f_M=\frac{3T}{\beta}\;\;\;,\;\;\;\lambda_M=\frac{c}{f_M}=\frac{b}{T}$$
이것이 바로 빈의 변위 법칙입니다.
정리($Q.M$) 1.1
[빈의 변위 법칙(Wien displacement law)]
$$\lambda_{\mathrm{max}}=\displaystyle\frac{b}{T}$$ 흑체가 방출하는 복사에너지에서 최대 세기의 파장($\lambda_{\mathrm{max}}$)은 흑체의 절대온도와 반비례한다. 여기서 상수는 $b=\displaystyle\frac{c\beta}{3}\simeq 2.897.8 \,\mathrm{\mu m\cdot K}$ 이다.
빈의 변위 법칙은 깔끔하게 유도되긴 하는데, 실제로는 문제점이 있습니다. 빈의 변위 법칙은 파장이 짧은 경우에는 성립하지만 파장이 긴 영역에서 실험 결과와 잘 맞지 않게 됩니다. 여기서 잘 맞지 않는다는 것은, 공식에 따르면 $\lambda_{\mathrm{max}}$ 값이 긴 경우에는 절대온도가 낮다는 뜻인데 실제 실험 결과 절대온도가 높아지는 것은 아니지만, 빈의 법칙에 의하면 파장이 길어짐에 따라 실제 실험 결과보다 온도가 더 빨리 감소하게 됩니다. 이론적으로 물리학에서 공식이 실험 결과와 맞지 않는다면, 그 공식을 먼저 의심하게 됩니다. 실험 결과에 맞는 물리적 법칙을 찾는 것이 물리학의 숙제이기 때문입니다.
빈의 법칙의 문제점은 나중에 플랑크의 제안으로 깔끔히 해결되게 됩니다. 하지만 그 전에, 레일리-진스 법칙에 대해서도 살펴보아야 합니다. 다음 글에서 다루도록 하겠습니다.
[참고문헌]
University Physics with Modern Physics, Pearson, Hugh D. Young, Roger A. Freedman
Quantum physics, Stephen Gasiorowicz, 3e
- 미소 부피 내에서 모든 방향으로 균일하게 에너지가 방출된다는 뜻. [본문으로]
'양자역학(Quantum Physics) > 배경, 기초' 카테고리의 다른 글
| 물질의 이중성과 파속의 도입(Duality of matter and introduction of wave packet) (0) | 2022.07.10 |
|---|---|
| 플랑크 법칙과 플랑크 곡선(Planck's law, Planck's curve) (0) | 2022.07.10 |
| 레일리-진스 법칙과 자외선 파탄(Rayleigh-Jean's law of radiation and Ultraviolet catastrophe) (0) | 2022.07.06 |
| 흑체복사(Black body radiation) (0) | 2022.07.06 |
| 양자역학의 시작 : 양자역학 등장 배경에 관한 설명 (0) | 2022.04.25 |




댓글