데카르트 곱을 정의하였으니 이제 그로부터 관계를 정의한 뒤, 동치관계와 동치류에 대해 설명해 보겠습니다. 동치관계의 개념은 앞으로 고학년에서 다룰 모든 수학의 과목에서 빈번히 등장합니다.
동치류와 동치관계의 개념을 정확히 설명하기 전에 다음 글을 꼭 기억하시기 바랍니다. 직관적인 이해를 위해 제가 만든 것입니다.

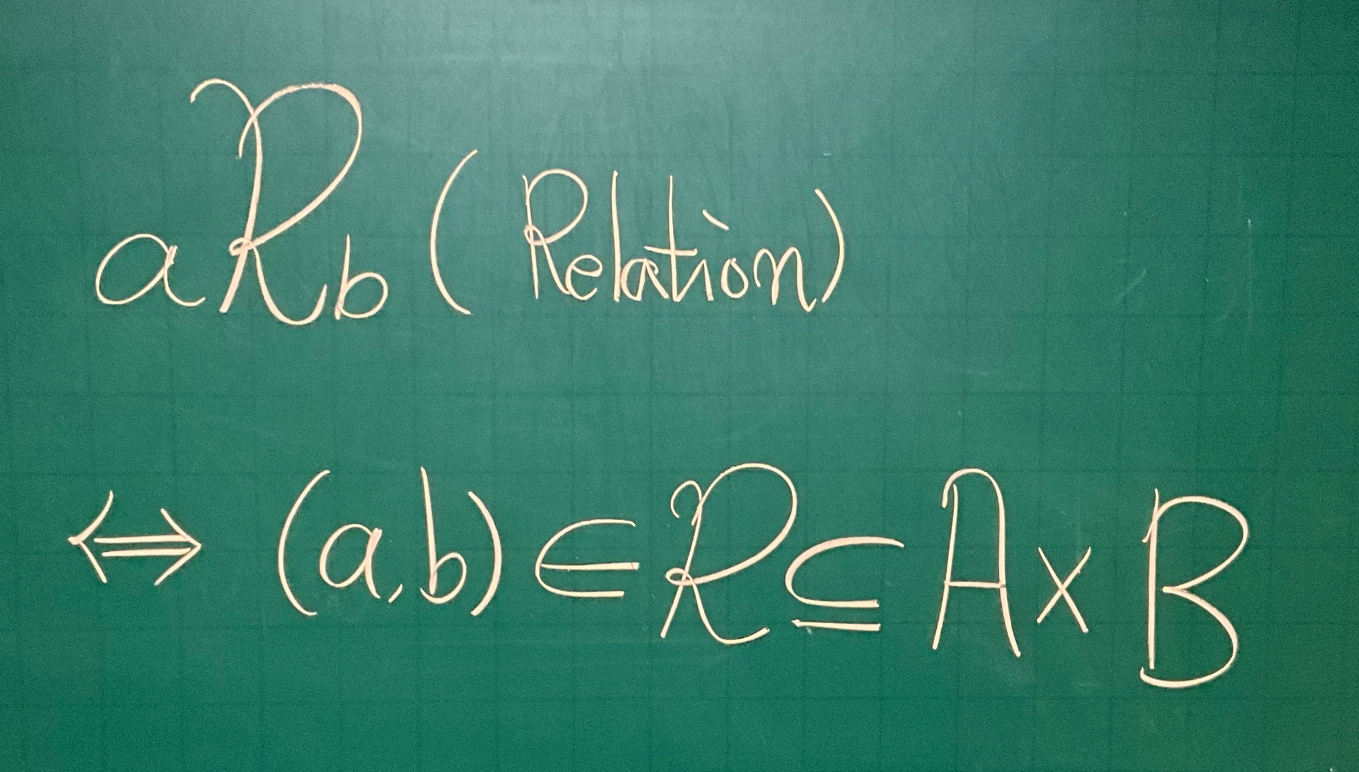
1. 관계
정의($S.T$) 3-2) 관계(Relations)
집합 $A$에서 $B$로의 '관계(relations)'란 $\mathcal{R}$ 로 표기하고, 두 집합의 데카르트 곱 $A\times B$ 의 하나의 부분집합에 해당한다. 이때 순서쌍 $(a,b)\in \mathcal{R}$ 을 $a\mathcal{R} b$ 로 나타낸다. 이는 '$a$ 가 $b$ 와 $\mathcal{R}$ 의 관계가 있다($a$ is $\mathcal{R}$-related to $b$)'라 읽는다. 정리하면 다음과 같다.
$$a\mathcal{R}b\;\Longleftrightarrow\; (a,b)\in \mathcal{R}\subseteq A\times B$$ 이고, $a\mathcal{R}b=(a,b)\notin R$ 이면 $a$는 $b$ 에 $R$ 의 관계가 없다고 한다.
관계는 데카르트 곱의 하나의 부분집합에 해당하며, 여기서 그 관계의 원소들인 순서쌍 $(a,b)\in \mathcal{R}$ 을 간단히 $a\mathcal{R}b$ 로 나타냅니다. 또한, 보통은 $A\times B$ 에서 두 집합이 같은 경우, 즉 $\mathcal{R}\subseteq X\times X$ 를 다루는 경우가 많은데 이는 간단히 $X$ 에서의 관계 $\mathcal{R}$($\mathcal{R}$ is a relation in $X)$ 라고 읽습니다.
정의($S.T$ 3-3) 역관계(Inverse relations)
집합 $A$ 에서의 $B$ 로의 관계 $\mathcal{R}$ 의 역관계(inverse)를 $\mathcal{R}^{-1}$ 로 나타낸다. 즉
$$b\mathcal{R}a\Leftrightarrow(b,a)\in\mathcal{R}^{-1}\subseteq B\times A$$ 와 같으며, 집합 표기로는
$$\mathcal{R}^{-1}=\left\{ (b,a)\mid(a,b)\in\mathcal{R} \right\}$$ 으로 나타낼 수 있다.
2. 동치관계
어떤 관계 $\mathcal{R}$ 이 다음과 같은 특별한 조건들을 만족시키는 특수한 관계에 대해 알아보려고 합니다.
정의($S.T$) 3-4) 동치관계(Equivalence relation)
공집합이 아닌 집합 $X$ 에서 관계 $\mathcal{R}$ 이 다음 세 가지 조건을 만족하면 $\mathcal{R}$ 을 '동치관계(equivalence relation)'이라고 부른다. 일반적으로 어떤 관계가 동치관계이면, $\mathcal{E}$ 라고 표기하는 편이다. 여기서 $x,y \in X$ 이다.
① 반사율(Reflexive) : 모든 $x\in X$ 에 대하여, $x\mathcal{R}x$
② 대칭률(Symmetric) : $x\mathcal{R}y \;\; \Rightarrow y\mathcal{R}x$
③ 추이율(Transitive) : $x\mathcal{R}y\,\wedge\, y\mathcal{R}z \;\; \Rightarrow \;\; x\mathcal{R}z$
직관적으로 생각해보면, 반사율은 모든 원소 자신이 자신과 순서쌍이 되었을 때, 즉 $(x,x)$ 라는 원소가, $X$에서 $X$로의 데카르트 곱의 한 부분집합 $\mathcal{R}$ 의 원소가 되어야 한다는 것이고, 대칭율은 $(x,y)\in \mathcal{R}$ 이면 $(y,x)\in \mathcal{R}$ 또한 성립해야 함을 뜻합니다. 추이율이 가장 헷갈릴 수 있는데, $(x,y)\in \mathcal{R}$ 이고 $(y,z)\in \mathcal{R}$ 임이 만족된다면 $(x,z)\in \mathcal{R}$ 또한 만족되어야 함을 뜻합니다. 이 동치관계는 처음 정의를 보면 낯설게 느껴지는 것이 당연합니다.
용어에 대해 설명을 간단히 하자면, 자기 자신과의 관계가 통하는 것은 그대로이니 반사적(reflexive)이라는 것이고, 대칭성은 서로 다른 두 원소에 대해서 위치를 바꾸니 대칭적(symmetric)이라는 것이며, 추이성은 a,b,c 순서로 타고 넘어간다는 이행의 의미가 짖습니다. 그래서 추이적(推移的, transitive)이라고 말합니다.
이 개념을 처음 들어보시는 분들은 도대체가 무엇을 말하고자 하는건지 납득하지 못해 어리둥절 할 것입니다. 동치관계라는 것은, 쉽게말해 세상에서 질적(qulity)으로 동질성을 가지는 관계를 말합니다. 세상(수학)에는 동일한 대상, 개념을 두고 여러가지 표현을 할 수 있습니다. 유리수라는 집합을 실수에서 무리수를 뺀 여집합으로 생각할 수도 있고, $\displaystyle\frac{q}{p}$ 꼴로 나타낼 수 있는 수로 말할 수도 있습니다. 심지어는 정수 집합의 임의의 두 수를 나누어 만든 숫자(단 0으로 나누진 않음)라 말하는 것도 가능하며, 분수꼴의 숫자는 비례식이나 나눗셈으로도 표현할 수 있고 이들은 모두 유리수를 나타내는 표현이 될 수 있지요. 따라서 이러한 관계들은 사실상 같은 대상을 뜻하는 것이고 이를 수학적, 논리적 도구를 써서 정의한 것이 바로 동치관계인 것입니다.1
그래서 동치류는 말하자면 동치관계라는 성질을 가진 '대표 원소'로 비유할 수 있는 뉘앙스를 가지고 있습니다. 예를 들어 여러분들은 초등학교를 졸업했다면
$$\frac{1}{2}=\frac{2}{4}=\frac{3}{6}=\cdots =\frac{100}{200}
\cdots $$
에 수긍하실 수 있을 것입니다. 그리고 $0.5$ 와 값이 같은 분수의 개수는 무한히 많다는 것도 알고 있을 것입니다. 그러면 이 모든 원소들은 본질은 같지만 마치 입고 있는 옷의 모양만 다르다고 비유할 수 있겠죠. 그래서, 이 원소들 모두를 앞으로 나타내기 보다도, 기약분수를 대표로 삼아 $\displaystyle\frac{1}{2}$ 를 사용할 수 있을 것입니다. 이때의 이러한 $ \displaystyle\frac{1}{2}$ 을 동치류라고 부르는 것입니다.
학부 수학의 집합론에서 동치관계와 동치류를 제대로 학습하지 않고 주먹구구식으로 암기하거나 겉핥기로 공부하면 추후 거대한 고생길을 고독히 걷게 될 가능성이 많습니다. 당장 2학년 정수론에 가면 합동의 개념을 이해하고 활용할 때 동치관계가 등장하고, 대수학 분야에서는 아예 원소들을 동치류로 대표하여 표현합니다. 위상수학에서는 겉보기에 모양이 다른 도형들을 동치관계를 통해 엮어 하나로 취급합니다.2 따라서 동치관계와 동치류를 집합론에서 시험을 잘 보기 위해 공부하는 수준을 넘어서, 까먹지 말고 졸업까지 머릿 속에 확실히 저장해두어야 미래 본인의 고전을 억제할 수 있을 것입니다.

수학 공부를 하다 보면 전혀 연관성을 찾을 수 없었거나 완전히 다른 개념이라고 생각했던 대상들이 탐색 과정을 거치면서 유기적으로 연결되어 있음을 깨닫는 경우가 많을텐데, 이와 같은 과정 속에서 서로 다른(것이라 생각했던) 개념들이 동치관계였음을 인지하는 순간이 발생할 것입니다. 그 때 명확한 동치관계의 정의인 위 세 가지 성질을 만족하는지 확인하면 동치관계 여부를 제대로 파악할 수 있게 됩니다.
예시를 몇가지 분석해 봅시다.
예제 1) $X=\left\{ 1,2,3 \right\}$ 에서의 하나의 관계 $\mathcal{R}=\left\{ (a,a),(b,b),(c,c),(a,b),(b,a)\right\}$ 는 동치관계임을 보여라.
sol) 각각의 $X$ 의 원소에 대해 반사율, 대칭률, 추이율을 따져 보면 됩니다.
① 반사율 : 모든 $X$의 원소에 대해 확인해야 하므로, $a,b,c$ 에 대해 모두 따져본다. 그러면 $(a,a)=a\mathcal{R} a \in \mathcal{R}$이고, $(b,b)=b\mathcal{R}b \in \mathcal{R}$ 이며, $(c,c)=c\mathcal{R}c \in \mathcal{R}$ 이 성립하므로 반사율을 충족한다.
② 대칭률 : 순서쌍의 앞과 뒤가 서로 다른 원소들에 대해서 모두 점검한다. $(a,b)=a\mathcal{R}b\in\mathcal{R}$ 이므로, $(b,a)=b\mathcal{R}a \in \mathcal{R}$ 인지를 확인해야 한다는 뜻이다. 이 조건이 성립한다. 반대로 $(b,a)=b\mathcal{R}a \in \mathcal{R}$ 이므로, $(a,b)=a\mathcal{R}b\in\mathcal{R}$ 인지 확인해야 하는데 참이기 때문에, 대칭률도 만족한다.
③ 추이율 : 두 개의 순서쌍을 뽑았을 때, 첫번째 순서쌍의 뒤쪽 좌표와 두번째 순서쌍의 첫째 좌표가 같은 모든 경우의 수를 따져준다. 이 각각의 경우에 대해서, 첫번째 순서쌍의 앞쪽 좌표와 두번째 순서쌍의 뒤쪽 좌표로 만들어진 순서쌍이 $\mathcal{R}$ 에 포함되어 있는지를 확인하면 된다.
1) $(a,a)$ 와 $(a,b)$ : $(a,a)=a\mathcal{R}a \in \mathcal{R}$ 이고 $(a,b)=a\mathcal{R}b \in \mathcal{R}$ 이므로, $(a,b)=a\mathcal{R}b \in \mathcal{R}$ 임을 확인하면 된다. 참이다.
2) $(b,b)$ 와 $(b,a)$ : $(b,b)=b\mathcal{R}b \in \mathcal{R}$ 이고 $(b,a)=b\mathcal{R}a \in \mathcal{R}$ 이므로, $(b,a)=b\mathcal{R}a\in\mathcal{R}$ 임을 확인하면 된다. 성립하므로, 참이다.
이외에는 없다. 따라서 주어진 관계 $\mathcal{R}$ 은 반사율, 대칭률, 추이율을 모두 만족하므로 동치관계이다. $_\blacksquare$
예제 2) 집합 $A=\left \{ a,b,c \right \}$ 에 대해 다음 두 관계 $R_1,R_2$가 동치관계인지 판별하여라.
$$R_1=\left \{ (a,a),(b,b),(c,c) \right \}
R_2=\left \{ (a,a),(b,b),(c,c),(a,b),(b,a),(a,c),(c,a) \right \}$$
sol) 관계는 이처럼 집합 형태로 주어지는 것이 일반적입니다. 그러면 '관계가 있다'의 뜻은 무엇이었나요? 바로 $(a,b)\in R$인 것입니다.
$R_1$의 경우, 동치관계입니다. $A$의 원소 하나에 대해서만 해볼까요? $c$를 골랐다고 합시다. 그러면 $(c,c)\in R_1$ 이므로 $c\sim c$입니다. 반사성은 만족합니다. 그 다음 지금 $R_1$에 들어가있는 순서쌍이 항상 같은 원소 들로만 이루어져 있으므로 대칭성과 추이성은 모두 자기 자신에 대해서만 적용할 수 있습니다. 무슨 뜻이냐면 예컨대 $(a,b)$ 과 같은 원소기 $R$에 있을 때 $(b,a)$가 있는지 확인하는 과정이 대칭성을 판별하는 것인데, 지금 $R_1$에는 모조리 $(x,x)\;x\in A$ 꼴의 원소만 있으니 대칭성과 추이성이 자동으로 만족되어 이미 동치관계란 것입니다.
$R_2$는 조금 다릅니다. $(a,a),(b,b),(c,c)$ 는 위에서 했으니 따질 필요도 없고,
$(a,b),(b,a)$는 반사성은 기본,
$(a,b)\in R_1\;\;\Rightarrow \;\;(b,a)\in R_1$ 이고 $(a,c)\in R_1\;\;\Rightarrow \;\;(c,a)\in R_1$ 이므로 이들은 대칭성은 만족합니다. 그러나, $(b,a)\in R_1\;,\;(a,c)\in R_1$ 인데 $(b,c)\notin R_1$ 이지요? 따라서 추이성을 만족하지는 않으니 $R_2$는 동치관계가 아닙니다. $_\blacksquare$
예제 3) [정수론과 대수학에서 매우 중요] 두 정수 $a,b$ 가 $n\mid (a-b)$, 즉 적당한 정수 $k$ 에 대하여 $a-b=nk$ ($n\in\mathbb{N},\,n\geq 2$ 3 ) 를 만족하면 두 정수는 '법(modulo) $n$ 에 관한 합동(congruence)' 4 이라고 부른다. 합동이 집합 $\mathbb{Z}$ 위에서 동치관계라는 것을 보여라.
Sol) 합동관계는 정수론과 대수학에서 굉장히 많이 다루기에 이것이 동치관계라는 사실을 집합론에서 처음에 잘 정리해 두는 것이 좋습니다. 그리고 저 식에서, $k$는 우리가 조절해서 넣을 수 있는 하나의 정수값이고, $n$은 2이상의 모든 자연수입니다. (각주를 참고하세요)
① 반사율 : $a\in\mathbb{Z}$ 에 대하여 $a-a=n\cdot k=n\cdot 0=0$ 이므로, 즉 $k=0$ 으로 선택하여 등식이 성립하기 때문에 $a\equiv a\;(\text{mod}\;n)$ 이다.
② 대칭률 : $a\equiv b\;(\text{mod}\;n)$ 이면 $b\equiv a\;(\text{mod}\;n)$ 이다. $k$ 대신 $-k\in\mathbb{Z}$ 를 택하면 되기 때문이다.
③ 추이율 : $a\equiv b\;(\text{mod}\;n)$ 이고 $b\equiv c\;(\text{mod}\;n)$ 가 성립하면, $a-b=k_1n$ 이고 $b-c=k_2n$ 이 성립하는 적당한 두 정수 $k_1, k_2$ 가 존재한다. 그러면 $a-c=(a-b)+(b-c)=(k_1+k_2)n$ 이며 $ (k_1+k_2)\in\mathbb{Z}$ 이므로, $a\equiv c\;(\text{mod}\;n) $ 이 성립한다. 따라서 합동관계 $\equiv$ 는 동치관계이다. $_\blacksquare$
어떤 공집합이 아닌 집합을 가지고 오더라도 최소한 두 개의 동치관계는 만들 수 있습니다. 첫번째 것은 관계가 데카르트 곱과 그냥 같은 집합일 때에 해당하고, 두번째의 경우 첫 좌표와 두번째 좌표가 동일한 순서쌍의 집합을 말합니다.
정리($S.T$) 3.2 동치관계의 최소 갯수
임의의 공집합이 아닌 집합 $X$ 에서의 동치관계는 적어도 다음 두 개는 존재한다.
① 자명관계(Trivial relation) : $R_T:=X\times X$
② 항등관계(Identitiy relation) : $R_I:=\left\{ (x,x)\mid x\in X \right\}$
증명) ① 이름 그대로, 자명하다. $R_T=X\times X$ 이면, 모든 $a\in X$ 에 대하여 $(a,a)\in R_T$ 이고, 임의의 $a,b\in X$ 에 대하여 $(a,b)\in R_T$ 이면 $(b,a)\in R_T$ 이다. $R_T=X\times X$ 이기 때문. 추이율도 자연스럽고 자명하게 만족한다. 그래서 $R_T=X\times X$ 는 동치관계이다.
② $R_I:=\left\{ (x,x)\mid x\in X \right\}$ 와 같이 정의하면, 모든 $a\in X$ 에 대해 순서쌍 $(a,a)\in R_I$ 이다. 반면 대칭률과 추이율의 경우, 이 관계 $R_I$ 는 오로지 앞 좌표와 뒤 좌표가 같은 순서쌍 $(a,a)$ 만을 취급하기 때문에, 대칭률과 추이율의 가정이 거짓이다. 조건문의 가정이 거짓이면 조건문의 진리값은 언제나 참이므로, $R_I$ 는 동치관계이다. $_\blacksquare$
항등관계를 증명할 때 대칭률과 추이율에 있어서는 조건문의 진리값에 대한 수리 논리 지식이 필요합니다. 또한 항등관계는 기하적으로 생각할 때 가로와 세로의 점들의 집합을 $X$라 두었을 때, 만들어지는 정사각형의 대각선들의 집합을 의미하게 됩니다. 순서쌍의 두 좌표가 항상 같으니까 마치 $y=x$ 그래프처럼 대각선 지점만을 의미하기 때문입니다. 그래서 '대각관계(diagonal relation)'이라 부르기도 합니다.
2. 동치류와 분할
정의($S.T$) 3-5) 동치류와 동치류의 집합
공집합이 아닌 집합 $X$ 위에서의 하나의 동치관계를 $\mathcal{E}$ 라 하자. 이때 각각의 $x\in X$ 에 대하여 집합
$$x/\mathcal{E}:=\left\{ y\in X\mid y\mathcal{E}x \right\}$$ 을 $x$에 의해 정해진 '동치류(equivalence class)'라고 한다. 또 이같은 $X$ 에서의 '동치류의 집합(set of equivalece classes)'은
$$X/\mathcal{E}:=\left\{ x/\mathcal{E}\mid x\in X \right\}$$ 으로 나타낸다.
수학에서 갑자기 어려워지는 경우는 흔히 몇가지 정의들이 마구 쏟아져 나올 때에 해당합니다. 동치류와 동치류의 집합에 관한 정의를 잘 이해해야 하는데, 사실 동치류 자체도 집합입니다. 그러니 동치류의 집합이란, 기본적으로 원소가 집합인 집합이라고 해석할 수 있습니다.
동치류의 정의를 보고 해석해 봅시다. 어떤 관계 $\mathcal{E}$ 에 대해서 순서쌍의 두번째 좌표가 $x$ 일 때, 순서쌍의 앞 좌표들을 끌어 모은 집합이 바로 $x$의 동치류에 해당하는 것으로 볼 수 있습니다. 즉, 어떤 순서쌍이 있을 때 뒤쪽 좌표에 대한 동치류는 앞쪽 좌표들을 모두 모은 집합에 해당한다는 것입니다.
예제 3') [대수학으로의 심화] 잉여류의 집합 $\mathbb{Z}_n$ 은 동치류인 '잉여류들(residue classes)'로 이루어진 집합이므로, 위 정의($S.T$) 3-5) 에서 $X/\mathcal{E}$ 에 대응되는 개념이다. 왜냐하면
$$\mathbb{Z}_n\cong \mathbb{Z}/n\mathbb{Z}$$
가 성립하기 때문이다. 예제 3) 에서 합동 $\equiv$ 가 동치관계임을 보였고, 따라서 합동을 동치관계로 생각할 때의 동치류가 존재하는데 그것이 바로 '법 $n$ 에 대한 잉여류(residue class of modulo $n$)'이 되는 것이다. 이들의 집합이 $\mathbb{Z}_n$ 이다. $_\blacksquare$
이 예제는 추상대수학을 공부할 때 요긴하게 쓰이며, 집합론과 대수학을 매끄럽게 연결합니다. 동치류의 집합은 추상대수학에서 잉여류(coset)들의 모임인 몫 군(Factor group)
$$G/K=\left\{ Kg\mid g\in G \right\}$$
을 바라볼 때 사용되는 관점으로 해석할 수도 있습니다. 여기서 $K$는 동치관계로, $K\unlhd G$ 이고 $G$ 는 군입니다. $Kg$ 는 우측 잉여류(right coset)입니다. 이것은 그 자체로 집합이기 때문에, 몫 군은 원소가 집합인 집합, 즉 집합족(family)입니다. 또한 이 잉여류들의 집합들은 $G$ 를 분할하게 되지요. 즉 몫 군과 잉여류의 개념은, 정확히 동치류의 집합 및 동치류에 대응되는 개념입니다.
아까 풀었던 예제를 통해 동치류에 대한 개념을 정리해 보겠습니다.
예제 4) 위의 예제 1)에서 $X=\left\{ 1,2,3 \right\}$ 에서의 하나의 관계 $\mathcal{R}=\left\{ (a,a),(b,b),(c,c),(a,b),(b,a)\right\}$ 는 동치관계임을 보였다. 여기서 $X$ 의 각 원소에 대한 동치류를 구하고 동치류의 집합을 찾아라.
Sol) $\mathcal{R}$ 이 동치관계이니까 모든 원소에 대해 각각 동치류를 구해봐야 합니다. 우선 $a/\mathcal{E}$ 라는 것은, 위에서 설명한 바와 같이 $a$가 두번째 좌표에 속해 있는 모든 순서쌍에 대하여 앞 좌표들을 모은 집합에 해당합니다. $a$가 두번째 좌표에 위치할 때의 순서쌍은 $\mathcal{R}$ 에서 $(a,a),(b,a)$ 뿐입니다. 따라서 $a/\mathcal{E}=\left\{ a,b \right\}$ 가 됩니다. 마찬가지로 $b/\mathcal{E}$ 를 구해보면 $b$가 순서쌍에서 두번째 좌표에 놓여 있을 때, 첫번째 좌표를 차지하는 모든 원소들의 모임이니 $b/\mathcal{E}=\left\{ a,b \right\}$ 입니다. $a,b$ 의 동치류는 사실 여기서 같네요. 마지막으로 $c$의 경우 순서쌍이 오로지 $(c,c)$ 밖에 없어서 $c/\mathcal{E}=\left\{ c \right\}$ 입니다.
따라서 동치류의 집합은
$$X/\mathcal{E}=\left\{ a/\mathcal{E},b/\mathcal{E},c/\mathcal{E} \right\}=\left\{ \left\{ a,b \right\} ,\left\{ c \right\}\right\}$$
가 되는 것입니다. 주의할 것은 위에서도 강조했지만 동치류 자체는 집합이며, 따라서 동치류의 집합은 원소들이 모두 집합인 것이지, 집합이 아닌 원소 표기를 하면 안됩니다. 즉 $X/\mathcal{E}=\left\{ a/\mathcal{E},b/\mathcal{E},c/\mathcal{E} \right\}=\left\{ a,b,c \right\}$ 라고 쓰면 틀립니다. $_\blacksquare$
재밌는 사실은 이 예제 4)에서 동치류의 집합의 원소들은, 그 자체로 $X$의 한 부분집합이 되는데, 그 부분집합들을 모으면 $X$를 완성시킬 수 있습니다. 이를 보고 동치류가 $X$를 분할한다고 표현합니다. $X/\mathcal{E}=\left\{ a/\mathcal{E},b/\mathcal{E},c/\mathcal{E} \right\}=\left\{ \left\{ a,b \right\} ,\left\{ c \right\}\right\}$ 에서, 동치류의 집합의 원소는 $X$를 몇가지 부분집합으로 쪼갰을 때 쪼개진 부분집합에 해당한다는 것입니다. 동치류와 분할에 대한 개념을 다음 글에서 정리해 보겠습니다.
[참고문헌]
You-Feng Lin, Shwu-Yeng T,Lin - Set thoery
- 위에서 말한 유리수를 정의하는 여러가지 방법이 있다는 비유에 대해서, 사실 유리수의 정의 자체는 하나로 보는 것이 적절하지만, 동어 반복을 통해 본질적으로 같은 대상을 표현하는 방법이 여럿 있다는 점에 주목하시기 바랍니다. [본문으로]
- 휴지 한 칸 = 휴지 곽 = 곽을 늘여 만든 도넛 [본문으로]
- 그러니까 $n$ 은 2이상의 모든 자연수가 다 들어갈 수 있다는 것입니다. 고정된 값이 아니라 2이상의 자연수 아무거나 다 넣었을 때 등식이 성립해야 합니다. [본문으로]
- 여기서 '법'이란, 법률의 '법'자가 맞는데, 수학에서 어떤 규칙을 법칙으로 하여 무언가를 만들 때 쓰는 전치사입니다. [본문으로]
'집합론(Set Theory) > 관계와 함수' 카테고리의 다른 글
| 함수의 엄밀한 정의(Definition of function in Set theory) (1) | 2023.12.15 |
|---|---|
| 두 집합의 데카르트 곱(Cartesian product of two sets) (0) | 2023.10.14 |
| 함수의 기본 개념 정리 (0) | 2020.12.17 |


댓글