▶ 여기서 설명하는 함수는 중고교 수준과 이를 넘어 대학교 미적분학 수준에서의 함수의 정의입니다.
이 글의 내용과 함수의 정의 수준 또한 논리적으로 전혀 문제가 없습니다.
하지만 만일 독자분이 다소 어렵더라도 엄밀한 정의를 알아보길 원하거나, 본격적으로 수학과에서 학습하는 집합론, 그리고 그 이상의 고난도 과목에서 다루는 엄밀한 함수의 정의를 알아보고 싶다면 이곳을 참고해 주시기 바랍니다.
1. 함수의 정의
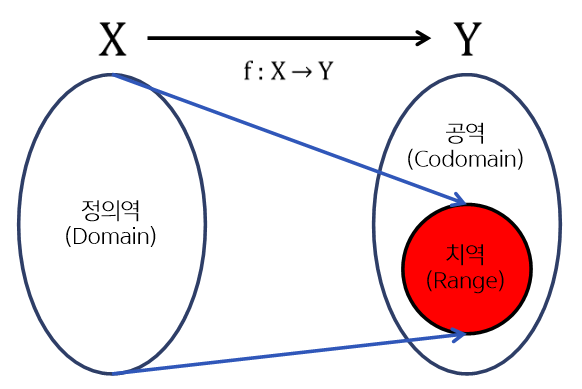
두 집합 $X,Y$에 대하여 $X$의 각 원소 $x$에 $Y$의 유일한 원소 $f(x)$를 대응시키는 규칙을 $X$에서 $Y$로 가는 '함수(function)' 또는 '사상(mapping)'이라 하고, $f:X\rightarrow Y$ 로 표기한다.
이 때 $X$와 $Y$를 각각 $f$의 '정의역(domain)', '공역(codomain)'이라 하고 집합 $\left \{ f(x)\mid x\in X \right \}$ 는 '치역(range)'이라 한다. 치역은 공역의 부분집합이다. 추가로 $f(x)$는 $f$에 의한 $x$의 상(image), $x$는 $f$에 의한 $f(x)$의 원상(preimage)라 한다.
2. 정의역, 치역, 공역의 관계에 의한 함수의 분류
'전사(全射, surjective)'는 $f$의 공역과 치역이 일치하는 함수이다. '위(上)로의 함수(onto)' 라고도 한다.
'단사(單射, injective)'는 임의의 $x_1,x_2\in X$ 에 대해 $f(x_1)=f(x_2)\;\;\Rightarrow x_1=x_2$ 인 함수 $f$를 말한다. '일대일 함수(one-to-one function)'이라고도 한다.
'전단사(全單射, bijective)'는 전사이고 단사인 함수이며 '일대일 대응(one-to-one correspondence)'이라고도 한다.
전사, 단사, 전단사는 영어보다 한국어 용어가 더 의미를 잘 표현하는 드문 용어에 속한다고 생각합니다. 적어둔 한자의 뜻을 알면 바로 함수의 특징을 해석할 수 있습니다.
전사는, 전부(全) 쏜다(射)는 뜻으로 정의역의 모든 원소가 공역의 모든 원소에 대응되는 함수를 뜻합니다. 그래서 치역과 공역이 같은 함수입니다.
단사는, 하나의 $x$값이 단 하나의(單) $y$값에 대응, 쏴진다(射)는 뜻입니다.
전단사는 전사(全射)이고 단사(單射)임을 뜻합니다. 역함수의 존재 조건과도 같습니다.
'집합론(Set Theory) > 관계와 함수' 카테고리의 다른 글
| 함수의 엄밀한 정의(Definition of function in Set theory) (1) | 2023.12.15 |
|---|---|
| 동치관계와 동치류(Equivalence relation, equivalence class) (1) | 2023.10.15 |
| 두 집합의 데카르트 곱(Cartesian product of two sets) (0) | 2023.10.14 |


댓글