잉여류는 대수학의 시작, 즉 군론에 입문할 때 반드시 알아야 하는 정수론의 개념입니다. 저는 정수론의 기초를 잘 모른 채 대수학 공부를 시작했었는데, 그 때문에 정말 골머리를 앓았던 기억이 생생합니다. 그런데 군론을 공부하고 나서 정수론의 개념 중 단 한가지만 제가 제대로 알고 넘어갔다면, 하는 후회가 남는 것이 바로 합동과 이 잉여류의 개념입니다. 달리 말하자면 여러분이 만일 정수론에 대한 빠삭한 학습 없이 대수학을 공부해야 한다면 합동과 잉여류에 대한 개념은 반드시 알아야 한다는 것입니다. 왜냐하면 군론을 다룰 때는 순환군과 더불어 $\mathbb{Z}_n$ 을 알아야 하고, 이것이 나중에 몫 군 $\mathbb{Z} / n\mathbb{Z}$ 과 동형(isomorphic)이라는 것을 보이게 되는데 이것이 다 합동에서 우러나오는 정수론의 즙이기 때문이죠.1
뿐만 아니라, 사실 정수론에서 이 잉여류(residue class)는 추상대수학에서 똑같이 잉여류(coset)로 번역하는 개념과 밀접한 관련이 있습니다. 대수학 버전이 좀 더 추상화와 일반화를 거친 개념에 해당합니다. 하지만 지금은 정수론이니, 대수학에서의 잉여류 개념은 마지막에 간단히만 적겠습니다.
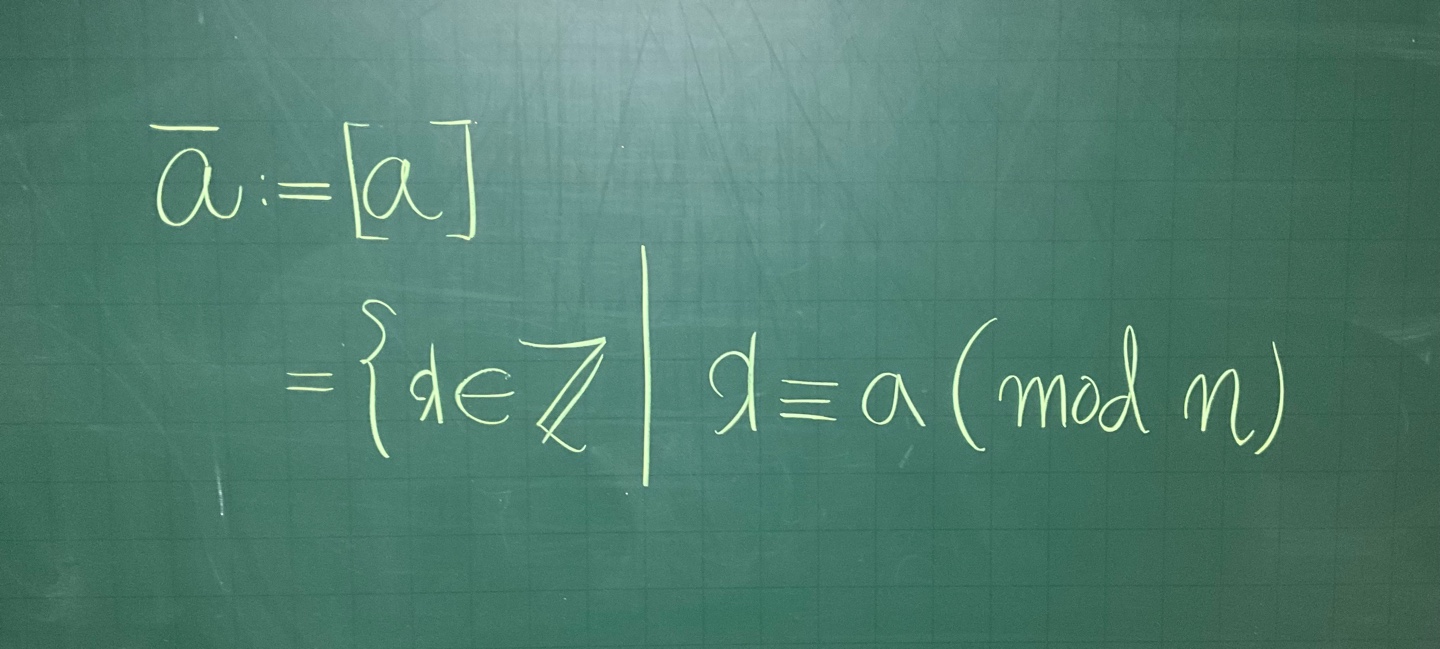
잉여류는 합동을 바탕으로 여러 원소들을 하나로 표현한다는 동치관계를 적용한 것으로 볼 수 있습니다. 그 글에서 저는 동치관계란 말하자면 '본질'이고, 동치류는 '대표원소'라는 말을 한 적이 있습니다. 우리가 오늘 다룰 잉여류라는 것은 일종의 동치류입니다. 즉 어떤 성질들을 만족하는 원소들이 수없이 존재할텐데 그들을 하나의 대표원소로 표현하겠다는 것이죠. 당연, 이 본질에 해당하는 성질은 합동과 관련된 것입니다.
합동의 정의를 다시 봅시다.
정의($N.T$) 3-1) 정수론에서 합동(Congruence)
어떤 자연수 $n$이 주어졌을 때, 정수 $a,b$ 가 다음을 만족할 때 $a$ 와 $b$는 법(modulo)2 $n$에 대해 합동이다'라고 말한다.
$$a\equiv b\mod n \;\;\Longleftrightarrow \;\;n\mid (a-b)$$
이것으로부터 유도되는 성질을 마치 동어 반복과 같이 나열하면, 아래와 같은 다섯 개의 TFAE 명제를 얻습니다.
정리($N.T$) 3.2)
TFAE : 다음은 전부 서로 동치이다
① $a\equiv b\;( \text{mod} \;\;n)$
② $a-b$ 는 $n$의 배수이다
③ $a-b=kn$ 을 만족하는 $k\in\mathbb{Z}$ 가 존재한다
④ $a$ 와 $b$ 는 $n$ 으로 나눴을 때 나머지가 동일하다.
⑤ $0\leq b < n$ 일 때는, $a$ 를 $n$ 으로 나눈 나머지가 $b$ 이다.
이 중 우리가 오늘 주목할 것은 ④번입니다. 도대체 왜 ④이 동치류와 연관된다는 것일까요?
1. 동치류는 대표원소라는 철학
④번은 $a$ 와 $b$ 가 법 $n$ 에 대해 합동이라면 $n$ 으로 나눈 나머지가 정확히 일치한다는 것을 보여줍니다. 나눗셈 알고리즘에 의해, 두 수의 나머지가 동일하다면 차를 구했을 때 나머지끼리 사라지게 될 것이므로 $kn$ $(k\in \mathbb{Z})$ 만 남아 $n$ 의 배수가 되어버리기 때문입니다.
이러한 성질은 종종 쓸모가 있습니다. 예를 들어 $7,12,17,22,27\cdots$ 은 $7$ 부터 시작해서 $5$ 씩 더한 숫자들입니다. 그러면 조건제시법으로 적으면 $A=\left\{ 5k+2\mid k\in\mathbb{Z} \right\}$ 와 같이 쓸 수 있습니다. 이렇게 적는 것은 중학교 또는 고등학교 수준의 수학에서도 가능합니다.
하지만 합동 개념을 알고 있는 우리 대학 수준에서는 보다 멋진 방법을 찾을 수 있습니다. 나열된 모든 숫자들은 $7$ 부터 시작해서 $5$ 의 배수들을 차근차근 더한 셈입니다. 이때 $5<7$ 이므로, 나눗셈 알고리즘의 불문율 $r<b$ 에 따라 $5$ 의 배수에 $7$ 을 더한 꼴인 $5k+7$ 대신 $5k+2$ 로 쓸 수도 있습니다.
하지만, 이는 또한 $5$ 로 나누었을 때 나머지가 $2$ 인 숫자들의 모임으로도 볼 수 있습니다. 그리고 이 관점이 우리가 지금 주목해야 할 부분입니다. 법(modulo)는 언제나 '나누는 수'에 해당함을 기억해 보자면, 이를 $n=5$ 를 택하는 상황으로 볼 수 있습니다. 잉여류 개념의 핵심은 바로 이것입니다 : 우리는 $ 7,12,17,22,27\cdots $ 를 전부 앞으로 $\overline{2}$ 로 표기할 것입니다. 동시에, ④의 개념까지 적용해보자면 $7,12,17,22,27\cdots $ 들 중 임의의 두 개를 선택하더라도 $5$ 로 나눈 나머지가 전부 $2$ 로 동일하며, $a-b$ 즉 이 숫자 중 임의의 두 개를 선택해서 차를 구하더라도 $5$ 로 나누어 떨어진다는 점에서 ②의 성질도 당연히 적용된다는 것을 알 수 있지요.
말하자면 주황색의 관점을 그대로 적용한 것이 잉여류이고, 초록색의 관점이 합동의 관점입니다. 정리($N.T$) 3.2) 에 의하면 이 둘은 동치이므로 결국 잉여류가 동치관계임을 보인다는 것은 합동이 동치관계를 보인다는 것과 대등합니다. 따라서 우리가 지금 정의할 잉여류는 동치관계임을 보일 수 있고, 이미 제가 다 설명했다고 생각하여 증명하지는 않을 것입니다.3
정의($N.T$) 3-4) 정수론에서 잉여류(residue class)
정수 $a$ 의 '법 $n$ 에 대한 잉여류(residue class modulo $n$)' 란 다음과 같이 정의하고 표기한다.
$$\overline{a}:=\left[ a \right]=\left\{ x\in\mathbb{Z}\mid x\equiv a \;(\text{mod}\; n) \right\}$$ 풀어서 설명하자면, $\overline{a}$ 는 법 $n$ 에 대해 정수 $a$ 와 합동인 모든 정수들을 모든 집합을 말한다.4
잉여류에서 문자가 헷갈려요 $\Longrightarrow$ 법 $n$ 은 '나누는 수'이고, 동치류(잉여류) $a$ 는 '나머지'다.
위 정의에서 종종 $n$ 과 $a$ 의 의미가 헷갈릴 때가 있습니다. 예컨대 위의 예시에서 저는 $7,12,17,22,27\cdots$ 가 법 $5$ 에 대한 $2$ 의 잉여류라고 하였으니, $\overline{2}$ 라고 적어야 합니다. 하지만 실수로 $\overline{5}$ 라 적지 않기 위한 방법이 무엇이 있을까요? 잉여(residue) 라는 것이 사실 말그대로 '나머지'를 뜻하는 다른 말입니다. 그래서, '나누는 수'는 언제나 법(modulo)이고, 그로 인해 발생한 부산물인 나머지가 바로 동치류인 잉여류에 해당한다는 원칙만 잘 기억하면 혼동을 방지할 수 있을 것으로 생각합니다.
예제 1) $n=2$ 일 때 $\overline{0}$ 과 $\overline{1}$ 을 조건제시법(Set-builder notation)으로 분석하여라
Sol) $n=2$ 로 나누었을 때 나머지가 $0$ 인 집합은 다음과 같다.
$$\overline{0}=\left\{ x\in\mathbb{Z}\mid x\equiv 0\;(\text{mod 2}) \right\}$$
따라서 이는 모든 짝수들의 집합이다. 반면, $2$ 로 나누었을 때 나머지가 $1$ 인 집합은
$$\overline{1}=\left\{ x\in\mathbb{Z}\mid x\equiv 1\;(\text{mod 2}) \right\}$$
이고, 이는 모든 홀수들의 집합이다. $_\blacksquare$
정리($N.T$) 3.5)
$n\geq 2$ 인 정수에 대하여, $\overline{a}=\overline{b}\;\Longleftrightarrow\; a\equiv b\;(\text{mod}\; n)$ 이다.
증명) $\Longrightarrow$ : $\overline{a}=\overline{b}$ 라 하자. $a\in \overline{a}$ 이므로, 정의에 의해 $a\equiv a\left( \text{mod}\;n \right)$ 이 성립한다. 그런데 $\overline{a}=\overline{b}$ 이므로 $a\in\overline{b}$ 이기도 하다. 그러면 $a\equiv b\left( \text{mod}\;n \right)$ 이 성립한다.
$\Longleftarrow$ : $\overline{a}\subseteq \overline{b}$ 와 $\overline{b}\subseteq \overline{a}$ 를 보임으로서 증명하자. 먼저 $x\in\overline{a}$ 이면, $x\equiv a \left( \text{mod}\;n \right)$ 를 뜻한다. 가정에 의해 $\overline{a}\equiv \overline{b}$ 이고 합동은 동치관계이므로 동치관계의 전이성(transitivity)에 의해 이는 결국 $x\equiv b \left( \text{mod}\;n \right)$ 임을 뜻한다. 따라서 $\overline{a}\subseteq \overline{b}$ 가 성립한다. 나머지 관계도 이와 똑같이 증명 가능하다. $_\blacksquare$
정리($N.T$) 3.6)
$n\geq 2$ 인 $n\in\mathbb{Z}$ 를 생각하자.
① $a\in\mathbb{Z}$ 이면, $\overline{a}=\overline{r}$ 가 성립하는 어떤 $0\leq r \leq n-1$ 인 $r\in \mathbb{N}$ 이 존재한다.
② 법 $n$ 에 대한 잉여류들은 정확히 서로 다른 $n-1$ 개, 즉 $\overline{0},\overline{1},\overline{2},\cdots \overline{n-1}$ 으로 존재한다.
증명) ②만 증명하면 충분하다. $\overline{r}=\overline{m}$ 이라 하고 $0\leq r,s \leq n-1$ 라 하자. $r\leq s$ 라 가정하자. 그러면 $0\leq s-r \leq n-1$ 이 성립한다.
그런데 $\overline{r}=\overline{s}$ 로부터 $r\equiv s\;(\text{mod n}$ 이므로 $0\leq s-r$ 는 $n$ 의 배수가 된다. 위의 $s-r$ 의 범위를 고려하면 $s-r=0$ 이 되어야 하고, 따라서 $s=r$ 이다. 즉 $\overline{r}=\overline{s}$ 이면 반드시 $s=r$ 이므로 법 $n$ 에 대한 모든 잉여류들 중 그 어느 것도 서로 같을 수 없다. $_\blacksquare$
①이 의미하는 것은, 만일 어떤 법 $n$ 에 대한 동치류를 $n-1$ 개 나열하게 되었을 때, 임의의 정수 $a\in\mathbb{Z}$ 를 데려왔을 때 이 $a$ 가 $n-1$ 개의 동치류 중 어느 하나에 반드시 속함을 의미합니다.
2. 잉여류들로 구성된 집합
잉여류들로 구성된 집합은 정수집합을 다룰 때 매우 중요합니다. 정수론보다 대수학의 군론, 환론의 단골손님이니 확실히 개념을 익히고 넘어갈 필요가 있습니다. 정수론만 당장 급히 학습하는 단계라면, 직접적으로 필요하지 않을 수 있으니 이 내용은 생략해도 좋습니다.
정의($N.T$) 3-5) 잉여류들로 구성된 집합(군의 연산이 덧셈)5
법 $n\in\mathbb{N}$ 이 주어졌을 때, 다음의 집합을 '법 $n$ 에 대한 정수 집합(Sets of integers modulo $n$)'이라고 정의한다. 이는 곧 법 $n$ 에 대한 모든 서로 다른 $n$ 개의 잉여류들을 원소로 갖는 집합을 말한다.
$$\begin{align*}
\mathbb{Z}_n&:=\left\{ \overline{a}\mid \overline{a}=
\left\{ x\in\mathbb{Z}\mid x\equiv a \;(\text{mod}\; n) \right\}\;,\;a\in\left\{ 0,1,2,\cdots n-1 \right\}
\right\}
\\\\&=\left\{\overline{0},\overline{1},\overline{2},\cdots \overline{n-1} \right\}
\end{align*}$$
잉여류에 대한 개념과 잉여류로 구성된 집합의 개념을 잘 구분해야 합니다. 잉여류는 동치류이니 그 자체로 '집합'입니다. 반면 잉여류들로 구성된 집합 $\mathbb{Z}_n$ 을 생각할 때는 이 집합의 원소가 잉여류이니, $\mathbb{Z}_n$ 은 집합들을 원소로 가진다는 것입니다.
아래 예제를 통해 명확한 개념 구분을 해봅시다.
예제 2) $\mathbb{Z}_7=\left\{ \overline{0},\overline{1},\overline{2},\cdots \overline{6} \right\}$ 에 대해 $13,20,41\in \mathbb{Z}_7$ 인가? 아니라면 어떻게 설명해야 하는가?
Sol) 문제가 잘못되었다. $13,20,41\notin \mathbb{Z}_n$ 이다. 정확히 말하면 $13,20,41$ 은 $\mathbb{Z}_7$ 의 원소인 잉여류에 속한다. 따라서 $13,20,41$ 이 어떤 $\mathbb{Z}_7$ 의 원소에 속하는지를 탐구해야 한다.
그런데 $13,20,41$ 은 공교롭게도 모두 주어진 법 $n=7$ 로 나누었을 때 나머지가 $6$ 으로 동일하다. 다시 말해 $13\equiv 6\; (\text{mod 7})$ 이고 $20\equiv 6\; (\text{mod 7})$ 이고 $41\equiv 6\; (\text{mod 7})$ 이다. 따라서 $13,20,41\in \overline{6}\in \mathbb{Z}_7$ 이다. $_\blacksquare$
예제 3) $\overline{48}$ 과 $\overline{-16}$ 은 $\mathbb{Z}_7$ 의 원소인가?
Sol) 정리($N.T$) 3.6) 을 이용하면 그렇다. $48\equiv 6\; (\text{mod 7})$ 이므로, $\overline{48}=\overline{6}$ 이다. 반면 $-16\equiv 5\; (\text{mod 7})$ 이므로 $\overline{-16}=\overline{5}$ 이다. $_\blacksquare$
음수에 대해 이 답이 $5$ 라는 것이 빨리 떠오르지 않는다면, 합동에서 연습을 충분히 하지 않았기 때문입니다. 합동에 관한 글의 예제3)-3)을 참고하시기 바랍니다. 그래도 친절히 설명을 해드리자면, $5$ 대신 $b$ 라는 문자를 두었다 생각해봅시다. 그러면 합동의 성질을 이용한다고 했을 때 $-16-b$ 가 $7$ 의 배수여야 합니다. 여기서 $-16$ 과 가장 가까운 $7$ 의 배수를 찾으면 $-14$ 와 $-21$ 인데, 제시된 $\mathbb{Z}_7$ 의 원소들은 $\overline{0}$ 부터 $\overline{6}$, 즉 양수인 $b$ 를 찾아야 하기 때문에 $-21$ 을 만들 수 있도록 $b=-2$ 대신 $b=5>0$ 을 택한 것입니다. 실제로 $\overline{5}=\overline{-2}$ 이죠?
3. 대수학으로의 확장
정의($A.A$) 2-?) 대수학에서 잉여류(cosets)
$G$ 가 군이고, $H\leqslant G$ 라 하자. 주어진(정해진 어떤) $g\in G$ 에 대하여,
① $H$ 의 '좌측 잉여류(left coset)'은
$$gH=\left\{ gh\mid h\in H \right\}$$ 라 정의한다.
② $H$ 의 '우측 잉여류(right coset)'은
$$Hg=\left\{ gh\mid h\in H \right\}$$ 로 정의한다.
여기서 연산이 무엇인지는 집합에 따라 달라지게 됩니다. 이 글에서 다룬 정수론에서의 법 $n$ 에 대한 잉여류의 개념과 비교하려면 연산이 덧셈이 되어야 합니다. 이때 대응 관계는 다음과 같습니다. 대수학-정수론 순서입니다.
$$G \longleftrightarrow \mathbb{Z}$$
$$H \longleftrightarrow n\mathbb{Z}$$
$$\overline{a} \longleftrightarrow g+H$$
$$g\in G \longleftrightarrow a\in \mathbb{Z}$$
고로 $g+H$ 라는 좌측 잉여류는 $\overline{a}=a+n\mathbb{Z}$ 로 나타낼 수 있고, 넘기면 $\overline{a}-a=n\mathbb{Z}$ 꼴이 됩니다.
이 상태에서 위에서 들었던 예시를 적용해봅시다. 아까 법 $n$ 에 대한 잉여류 설명을 할 때 $n=5$ 로 택하고 $a=2$ 를 사용했으므로, 대수학의 잉여류 개념을 활용하면 $\overline{2}=2+5\mathbb{Z}$ 가 됩니다.
좌변부터 해석합시다. 좌변은 순수 정수론입니다. $\overline{2}$ 의 값, 곧 법 $n=5$ 에 대한 $2$ 의 잉여류란 $5$ 로 나누었을 때 나머지가 $2$ 인 숫자들의 집합임을 뜻합니다. 이는 $7,12,17,22,27,\cdots $ 에 해당하지요.
우변을 보면 $2+5\mathbb{Z}$ 이고, 여기서 우변의 두번째 항인 $5\mathbb{Z}$ 는 $H$ 의 역할로서 $\mathbb{Z}$ 의 부분군이며, 모든 원소가 다 들어갈 수 있습니다. 따라서 $\cdots -1,0,1,2,3,\cdots $ 이렇게 다 대입을 한다고 가정해보면, 똑같이 $7,12,17,22,27,\cdots $ 를 얻습니다. 6
재밌는 것은 이때 좌측 잉여류와 우측 잉여류가 같으니,7 $5\mathbb{Z}\unlhd \mathbb{Z}$, 즉 정수 집합의 정규 부분군(normal subgroup)이 된다는 것입니다. 물론 $5\mathbb{Z}$ 는 애초에 아벨군 $\mathbb{Z}$ 의 부분군이니 $5\mathbb{Z}$ 가 정규 부분군이라는 것을 굳이 이렇게 보일 필요는 없지만, 따지고 보면 이 과정을 통해서도 확인 가능하다는 것이죠.
[참고문헌]
Introduction to Abstract Algebra, 4e, W.Keith Nicholson
- 앗, 근데 만일 1학년에 노느라 집합론의 동치관계 및 동치류를 제대로 보지 않았다면... 당연한 말이지만 그것부터 제대로 챙기고 오셔야 합니다. [본문으로]
- 복수형은 moduli [본문으로]
- 합동이 동치관계인 것은 이미 집합론의 동치관계와 동치류 글에서 증명했습니다. [본문으로]
- 당연히 $a$ 자기 자신도 포함합니다. $a\mathcal{R}a$ [본문으로]
- 정수론에서 당장 군의 연산이 무엇을 의미하는지 알 필요는 없습니다. 이 개념은 대수학에서 중요합니다. [본문으로]
- 물론 좌변이나 우변이나, $7$보다 작은 숫자들도 무수히 많이 포함되어 있지만 귀찮아서 그냥 스타트를 $7$ 로 정한 것일 뿐입니다. 실제로는 음수도 다 포함되지요. [본문으로]
- 참고로 여기서 좌측 잉여류와 우측 잉여류가 군인 것은 아닙니다. [본문으로]
'정수론(Number Theory) > 합동 이론' 카테고리의 다른 글
| 정수론의 합동에서 동치류들의 연산 (0) | 2024.06.29 |
|---|---|
| 합동방정식(congruence equation) (0) | 2024.06.27 |
| 합동의 연산성질(Operations on congruence in the Number Theory) (1) | 2024.06.24 |
| 정수론에서 합동(Congruence) (1) | 2024.01.10 |




댓글