복소수의 거듭제곱근과 드 무아브르의 정리(Powers and Roots of Complex number and De Moivre's Theorem)

이번 시간에는 복소수의 거듭제곱과 거듭제곱근을 다루어 보겠습니다. 약간 난이도가 올라가면서도 복소해석의 후반부에 등장하는 매우 중요한 적분 테크닉에 다시 등장할만큼 중요한 개념이고 이것 자체가 복소수가 갖는 유별난 특징이기 때문에 머리에 힘을 좀 주는 것이 필요합니다.

---

 

1. 복소수의 $n$ 제곱근

 

1) 드 무아브르의 정리

 

정리($C.N$) 1.4) 드 무아브르의 정리
복소수 $z$ 를 $n$ 제곱 하면,
$$z^n=\left( re^{i\theta} \right)^n=r^n\left( \cos \theta +i\sin\theta \right)^n=r^n\left( \cos n\theta +i\sin n\theta \right)$$ 을 얻는다. 여기서 $\left( \cos\theta+i\sin\theta \right)^n=\left( \cos n\theta + i\sin n\theta \right)$ 의 관계를 '드 무아브르의 정리(De Moivre's Theorem)'이라고 한다.
반면 복소수 $z$ 에 $\displaystyle\frac{1}{n}$ 승을 취하면
$$z^{\frac{1}{n}}=\left( re^{i\theta} \right)^{\frac{1}{n}}=\sqrt[n]{r}\left( \cos\frac{\theta}{n}+i\sin\frac{\theta}{n} \right)\;\;\;\cdots \;\;\;(1)$$

 

복소수의 $n$제곱은 크기를 $n$제곱하고 각도에 $n$을 곱하는 것으로 해석할 수 있습니다. 즉 원점으로부터의 점까지의 팔 거리는 길어지고, 각도는 더 많이 회전하게 되는 셈입니다.

 

반면에 $\displaystyle\frac{1}{n}$ 제곱을 씌우는 경우 크기 $r$ 도 그만큼 줄어들고,  각도도 $\displaystyle\frac{1}{n}$ 배 덜 회전하게 됨을 알 수 있습니다.

 

그런데 이 때는 단순 $n$ 제곱을 할 때와 달리 주의해야 할 점이 발생합니다. 원래 극좌표에서는 $360$도를 회전할 때마다 위치가 동일해지기 때문에 순환성을 가집니다. 예를 들어 (제곱근을 씌우지 않은) 오리지널 복소수가 $z=re^{i\theta}=re^{i\left( \theta+2m\pi \right)}\;\;\; (m\in \mathbb{Z})$  로 표현된다고 해도, 두번째 항의 값이나 세번째 항이 가리키는 점 그리고 값은 같습니다. 30도를 돌거나, 360+30도를 돌거나, 720+30도를 돌아도 같은 지점으로 돌아오기 때문입니다. 마치 회전목마를 타면서 같은 위치에서 기다리는 부모님을 여러번 돌아도 동일한 위치에서 동일한 시야를 통해 볼 수 있는 것처럼 말입니다.

 

그러나 지수에 $\displaystyle\frac{1}{n}$ 을 취하면 이런 일종의 규칙성이 깨집니다. 공식에 의하면 돌린 각도는 원래 각도를 $n$으로 나눈 $\displaystyle\frac{\theta}{n}$ 으로 변화합니다. 그런데, 나누기 전에는 점이나 값이 30도 = 360+30도 였지만 이를 같은 수로 나누게 된다면? 만일 두 값을 3으로 똑같이 나누면

 

$$\frac{30}{3}=10\neq \frac{360+30}{3}=130$$
이 됩니다. 즉 동일한 $z$값을 나타냈던 여러 표현은 만일 거듭제곱근을 취하게 되면 각기 다른 값이 된다는 뜻입니다. 이것이 바로 '다가함수(Multi-Valued function, Multifunction)'의 개념이며 거듭제곱에 쓰일 주어진 $n$의 값에 따라 복소수 $z^{\displaystyle\frac{1}{n}}$ 의 값은 ($m$ 때문에) 2개 이상이 될 수 있음을 뜻합니다. 다가함수의 개념은 이후에 고도의 복소적분을 수행하기 위해 다룰 가지 자름(Branch cut)이란 무시무시한 녀석이 등장할 때 이해의 필수 조건이니 꼭 머리 한구석에 기억해두셔야 합니다. 이와 같은 개념을 이제 체계적으로 정리해 봅시다.

 

 

2) 복소수의 $n$ 제곱근

 

 

정리($C.N$) 1.5) 두 복소수가 같을 조건
두 복소수 $z_1=r_1e^{i\theta_1}$ 과 $z_2=r_2e^{i\theta_2}$ 를 생각하자. $z_1=z_2$ 이기 위한 필요충분조건은 $r_1=r_2$ 이고 $\theta_1=\theta_2+2k\pi\;(k\in\mathbb{Z})$ 인 것이다.

 

제곱근을 다루기 전에 뜬금없이 이와 같은 성질을 정리한 이유가 있습니다. 잠시 중고등학교 수학으로 돌아가, 어떤 실수 $a$ 의 $n$ 제곱근은 몇 개인지 따져보았던 기억의 세계로 빠져들어가 봅시다. 그러면 당황하지 말고 기계처럼 다음을 외쳐야 합니다.

 

$a$ 의 $n$ 제곱근을 찾는 문제는 방정식 $x^n=a$ 의 실근을 떠올린다.

1) $n$ 이 짝수일 때와 홀수일 때로 나누고, 그에 따라 $a$ 의 부호까지 떠올린다.
2) $n$ 이 짝수이면, $a>0$ 일 때 2개, $a=0$ 일 때 1개, $a<0$ 일 때 실근이 없다. 허근이 두 개 존재한다.
3) $n$ 이 홀수이면, $a$ 의 부호와 관계없이 항상 1개의 실근이 존재한다.

 

 

이때 $x,a$ 만을 복소수로 바꾼 것이 우리가 지금 다룰 내용입니다. 만일 이들이 복소수로 달라지게 된다면 간단히 말해 그냥 허근까지 세면 된다는 문제에 도달하게 됩니다. 그리고, 실근에서는 $n$ 의 홀짝성에 따라, 또 $a$ 값에 따라 실근의 개수가 변화했지만 복소수 범위에서 근을 고려한다면 항상 $n$ 제곱근에 대해서 근이 $n$ 개 존재한다는 것을 예상할 수 있을 것입니다. 실근과 허근이 아닌 근은 존재하지 않기 때문이죠. 고로 허근까지 카운팅을 한다면, 정확히 $n$ 개 존재합니다.^[각주:1]

 

그렇다면 이제 $x^n=a$ 를 복소수 버전으로 바꾸어 $z^n=z_0$ 와 같이 나타나는 방정식을 고려해 봅시다. 여기서 $z=re^{i\theta}$ 이라 하고 $z_0=r_0e^{i\theta_0}$ 로 잡습니다. 그러면 두 수가 같다는 것은 정리($C.N$) 1.5) 에 의하여

 

$$r^n=r_0\;,\; i n\theta = \theta_0+2k\pi\;\;(k\in\mathbb{Z})$$

 

이때 복소수의 크기(modulus)는 반드시 양수이므로 $r=\sqrt[n]{r_0}$ 와 같이 $r$ 은 $r_0$ 의 양의 $n$ 제곱근이 됩니다. 반면 각도는

 

$$\theta = \displaystyle \frac{\theta_0+2k\pi}{n}=\displaystyle \frac{\theta_0}{n} +\displaystyle \frac{2k\pi }{n} \;\;(k\in\mathbb{Z})$$

 

가 되어, $z_0$ 의 모든 $n$ 제곱근들은

 

$$z= (z_0)^{\frac{1}{n}}=\sqrt[n]{r_0}\,e^{i\left( 
\displaystyle \frac{\theta_0}{n} +\displaystyle \frac{2k\pi }{n} \right)}\;\;\;(k\in\mathbb{Z})$$

으로 나타낼 수 있게 됩니다. 여기서 관찰할 것은 각도 부분을 보면, 각은 $\displaystyle\frac{\theta_0}{n}$ 을 시점으로 하여 계속해서 $2\pi \cdot \displaystyle\frac{1}{n}$ 만큼 추가되는 상황입니다. $2\pi$ 는 한 바퀴이고, 그렇기에 이를 $n$ 으로 나누게 되면 적당한 정해진 호의 길이만큼을 주기로 계속 돌게 된다는 것입니다. 여기까지의 결과를 정리해 봅시다.

 

 

정리($C.N$) 1.6) 복소수의 $n$ 제곱근
두 복소수 $z=re^{i\theta}$ 와 $z_0=r_0e^{i\theta_0}$ 를 생각하자. $z_0$ 의 $n$ 제곱근은 방정식 $z^n=z_0$ 의 근 $z$ 값을 말하고, 그 값은
$$z= (z_0)^{\frac{1}{n}}=\sqrt[n]{r_0}\,e^{i\left( 
\displaystyle \frac{\theta_0}{n} +\displaystyle \frac{2k\pi }{n} \right)}\;\;\;(k\in\mathbb{Z})$$ 으로 나타낼 수 있다. 이 값의 개수는 정확히 $n$ 개이고 무한히 많은데 반복되기 때문에, 서로 다른 $n$ 제곱들을 $c_k$ 라 하면
$$c_k=\sqrt[n]{r_0}\,e^{i\left( 
\displaystyle \frac{\theta_0}{n} +\displaystyle \frac{2k\pi }{n} \right)}\;\;\;(k=0,1,2,\cdots , n-1)$$ 와 같이 나타낼 수 있다.

정의($C.N$) 1-6) 주 $n$ 제곱근
① $\theta_0=\mathrm{Arg}\, z_0$ 일 때, 다시말해 $\theta_0$ 가 $\arg z$ 의 주 값일 땐 $c_0=\sqrt[n]{r_0}\,e^{i\left( \displaystyle \frac{\theta_0}{n} \right)}$ 을 $z_0$ 의 '주 $n$ 제곱근(principal root)'이라고 한다.
② $\omega_n = e^{i\left( \displaystyle\frac{2\pi }{n} \right)}$ 이라고 정의하자. 이 $\omega_n$ 은 반시계방향으로 $\left( \displaystyle\frac{2\pi}{n} \right)$ 만큼의 회전을 의미하는 값이다. 그러면
$$\omega_n^k = e^{i\left( \displaystyle\frac{2k\pi }{n} \right)}\;\;\;(k=0,1,2,\cdots , n-1)$$ 과 같이 정리할 수 있고, 이를 바탕으로 
$$c_k=c_0\omega_n^k=\sqrt[n]{r_0}\,e^{i\left( 
\displaystyle \frac{\theta_0}{n} +\displaystyle \frac{2k\pi }{n} \right)}\;\;\;(k=0,1,2,\cdots , n-1)$$ 와 같이 적을 수 있다. 즉 $z_0$ 의 모든 서로 다른 $n$ 제곱근들은 이 표현으로 하면 $c_0\omega_n\;,\;c_0\omega_n^2\;,\; \cdots \;,\; c_0\omega_n^{n-1}$ 이다.

 

예제를 하나는 풀어보고 갑시다.

---

예제 1) 8의 세제곱근을 복소수 범위로 확장해서 모두 구하여라.


Sol) 실수 범위에서만 따지면 8의 세제곱근은 2 한개밖에 존재하지 않습니다. 그러나 복소수로 확장하면 몇가지 더 찾을 수 있을 것이며 위 정리 결과에 의하면 3개가 존재할 것이라 예상할 수 있을 것입니다. 우선 복소수의 Power, root 공식을 이용해서 세제곱근을 달아봅시다.

$$8^{\frac{1}{3}}=r^{\frac{1}{3}}e^{\frac{i\theta}{3}}$$
그러면 $r$과 $\theta$ 를 찾는 것이 목적이 됩니다. 이것을 구하는 방법은 아래 원칙을 적용하면 됩니다.

1) $r$을 찾는 방법 : 주어진 숫자의 실수 제곱근을 구한다. (단, 이 때 부호는 양수로 생각한다. 즉 $r$은 애초에 정의상 양수이다.)

본 문제에서 8의 실수 세제곱근은 2입니다. 즉 우리가 구하는 $r$값은 2입니다. (만약 -8의 세제곱근을 구하는 문제라면? $r$은 항상 부호가 양수이기 때문에 이 때도 $r$은 2입니다. 괄호 안의 '이 때 부호는 고려하지 않는다'가 바로 이러한 의미입니다.


2) $\theta$ 를 찾는 방법 : 주어진 숫자를 복소평면에 찍고, 극좌표에서의 각도를 셈한다.

주어진 숫자는 8이고, 이것을 복소 평면에 찍으면 허수 부분은 0이고 실수 부분의 값이 8이니 $x$축에 원점으로부터 거리가 8인 지점에 찍히게 됩니다. 그러면 이 때 극좌표 표현 방식에서 각도 $\theta$ 는

$$\theta=0,\,2\pi,\,4\pi,\,\cdots$$
가 되지요.

근데 이건 8을 복소수로 나타냈을 때의 $\theta$ 값이지 $8^{\frac{1}{3}}$ 의 각도값이 아닙니다. 다시 말해

$$z=8=2e^{i\theta}=2e^{0}=2e^{2i\pi}=2e^{4i\pi}\;\;\;\cdots$$
라는 뜻이지요. 우리는 $8^{\frac{1}{3}}$ 을 구하기를 원하므로 이 각도에 $\displaystyle\frac{1}{3}$ 배를 해야 합니다. 그러므로 8의 세제곱근 값들은 다음과 같이 3개가 나옵니다.

$$\begin{align*}
8^{\frac{1}{3}}

&=2e^{0}=2

\\\\\\&=2e^{\frac{2i\pi}{3}}=2\left( \cos \frac{2\pi}{3}+i\sin \frac{2\pi}{3} \right)=-1+i\sqrt{3}
\\\\\\&=2e^{\frac{4i\pi}{3}}=2\left( \cos \frac{4\pi}{3}+i\sin \frac{4\pi}{3} \right)=-1-i\sqrt{3}
\end{align*}$$
여기서 $6\pi,\,8\pi \cdots $ 는 왜 다 셈하지 않느냐하는 의문이 들 수 있는데, 실제로 그들을 계산해보면 저 3개의 값에서 로테이션이 발생함을 알 수 있습니다. 이는 아래서 곧 만나게 될 [그림 1]처럼 원을 그려놓고 보면 저 세개의 점만 계속 찍힌다는 사실로부터도 알 수 있습니다. 그래서 정답은 오로지 위 3개만 존재하는 것입니다. $_\blacksquare$

 

 

 

3) 다가함수의 발생

 

보조정리($C.A$) 1.1) $n$ 제곱근의 다가성
$z$ 를 나타냈던 여러 표현들, 즉 각의 순환성(주기성) 때문에 발생했던 표현들은 $n$의 거듭제곱근을 취하면 값이 달라질 수 있다. 곧, 등식
$$z=re^{i\theta}=re^{i\left( \theta\pm 2\pi \right)}=re^{i\left( \theta\pm 4\pi \right)}=\cdots$$ 의 각 모든 변에 거듭제곱근 $\displaystyle\frac{1}{n}$ 을 씌웠을 때, 이 등호가 유지되지 않을 수 있게 된다는 것이다.

정의($C.N$) 1-7) 다가(多價)함수
복소수 집합을 정의역과 공역으로 삼는 함수 $f:\mathbb{C}\longrightarrow \mathbb{C}$ 가 $z\longmapsto \sqrt{z}=z^{\frac{1}{2}}$ 로 정의된 경우를 생각하자. 그러면 $f$ 의 정의역의 한 원소가 서로 다른 $n$ 개의 공역의 원소로 대응될 수 있기 때문에 전통적인 의미에서 이는 함수의 정의를 만족시키지 않지만, 이러한 함수 $f$ 는 관례적으로 '다가함수(multi-valued function or simply multifunction)'이라고 부른다. 가장 대표적인 다가함수는 거듭제곱 함수이다.

 

다가함수 개념은 뒤쪽에서 유수정리와 같은 고난이도 테크닉을 사용해 복소적분을 할 때 '분지절단(branch cut)'의 개념을 이해하기 위해 반드시 필요한 도구입니다. 하지만 다가함수의 개념 자체는 특별한 적분과 관련있는 것이 아니라 단순히 복소수의 $n$ 제곱근에 바탕을 두고 있는 것이기 때문에 지금 소개하는 것입니다.

 

복소수는 $n$ 제곱근을 달아 주었을 때, 보조정리($C.N$) 1.1) 에서 말하는 것처럼 등호 관계가 박살날 수 있습니다. 예를 들어 아래 [그림 1] 을 봅시다. $(a)$ 의 case 부터 보게 되면, 복소수 관점에서 $1^{\frac{1}{3}}$ 을 구하면 $1$ 만을 떠올리기 십상이지만 복소수 범위에서 $1$ 은 대표값(주 값)일 뿐이고 실제로는 3개나 존재합니다.

 

[그림 1] 여러가지 값들의 1/3 제곱근의 값. 복소수 범위로 늘리면 이처럼 허수단위 $i$를 포함한 세가지 값이 존재한다. 참고로 'cube root'는 세제곱근의 영어 표현이다.

 

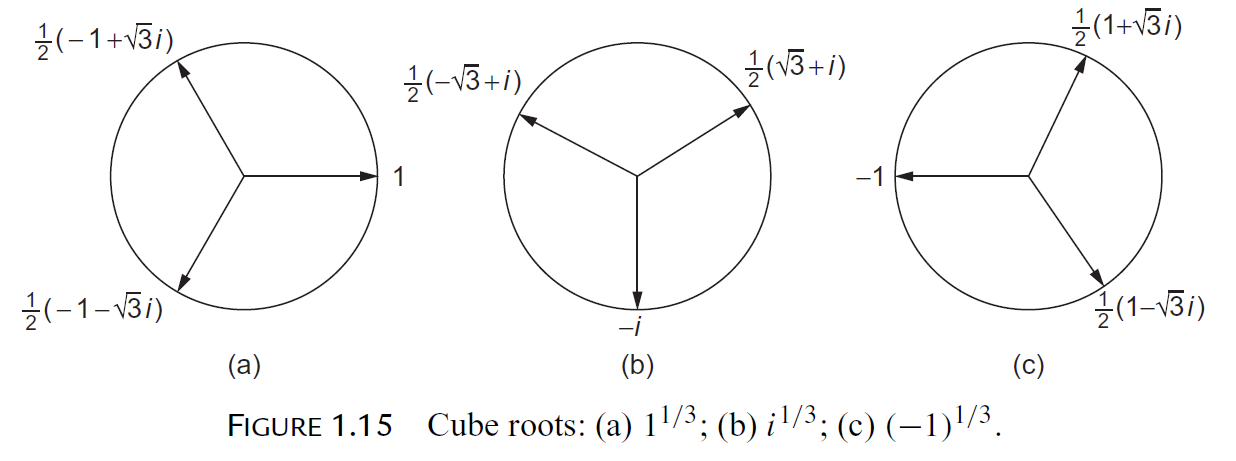
나머지 $(b),(c)$ 또한 같이 검토해보면, 주 제곱근 값은 순서대로 $1,-i,-1$ 임은 쉽게 눈치챌 수 있을 것입니다.

 

그런데 $(a)$ 에서 $1$ 이라는 수를 표현할 때, $1=e^{i\cdot 0}=e^{i\cdot 0+2\pi}=e^{i\cdot 0+4\pi}=\cdots$ 과 같이 계속해서 $2k\pi \;\;(k\in\mathbb{Z})$ 를 더하는 형식을 지수에 올려 넣어도 등호가 성립합니다. 복소평면에서 $(1,0)$ 이라는 점은, 중심이 원점이고 반지름이 $1$ 인 원 위에서 임의의 정수 바퀴를 돌더라도 제자리로 돌아오기 때문입니다. 그러나 문제는 만일 여기에 $\displaystyle\frac{1}{3}$ 이라고 $n$ 제곱근을 씌워주는 순간 3가지 종류의 값으로 쪼개지게 된다는 것입니다. 그러면 등호는 3값을 주기로만 유지되고, 나머지 등호들은 전부 박살나게 되는 것이지요. 따라서 만일 $z\in\mathbb{C}$ 를 $z^{\displaystyle\frac{1}{3}}\in\mathbb{C}$ 로 보내는 함수 $g$ 가 있다고 생각하면, 전통적 의미에서 이것은 함수가 되지 않습니다.

 

하지만 왜 '다가함수'라는 이름을 붙여주어서 Semi 함수처럼 취급을 해주는 것일까요? 이는, 예를 들어 주 값(principle value)만을 활용하면 함수처럼 다룰 수 있게 되기 때문입니다. 위에서 본 예제 1)의 답을 관찰하면 $8^{\frac{1}{3}}$ 의 값이 $2$, $-1+i\sqrt{3}$, 그리고 $-1-i\sqrt{3}$ 임을 확인했습니다. 그리고 이들은 극 형식으로 나타내었을 때 각각 $2e^0$, $2e^{\frac{2i\pi}{3}}$, $2e^{\frac{2i\pi}{3}}$ 에 해당했습니다. 그리고 지수에 $6\pi, 8\pi,\cdots$ 를 계속 넣어도 그 값은 이 셋에서 벗어나지 않게 됩니다. 그렇다면 만일 여기서 각도의 범위를 $0\leq \theta \leq 4\pi$ 로 조여주게 된다면? 그렇다면 더 이상 정의역의 한 원소가 여러 원소로 대응되지 않도록 조작할 수 있게 된다는 뜻입니다. 물론, 여전이 $8$ 을 $8^{\displaystyle\frac{1}{3}}$ 으로 보내면 세 값 중 하나는 선택해야 하기는 하지만, 셋 중 하나를 선택한 뒤 각의 범위를 조여줌으로서 함수처럼 바꿀 수 있다는 것입니다.

 

실제로 이렇게 한 세트(위에서는 3개)를 가진 하나의 주기는 '리만평면(Riemann sheet)'의 근본적 개념이고, 이어지는 리만평면을 하나씩 잘라서 적분하는 테크닉을 복소해석학 후반부에 다루게 될 것입니다.

 

 

 

 

 

[참고문헌 ]

Mathematical methods for Physicists, 7e, Arfken & Weber & Harris

Complex variables and applications, James Ward Brown & Ruel V. Churchill, 9e

 

 

 

 

1. 이에 관한 정리는 대수학의 기본정리라고 부르는 것으로 대수학에서 증명합니다. 아니면 복소해석학 후반부에서 다룰 수 있는 도구를 배우게 될 것입니다. 그러니 지금 당장은 연역적으로 깔끔하게 증명하기 까다롭기에, 경험적인 사실로부터 이해하고 받아들이는 수준에서 머물러야 합니다. [본문으로]