3차원 양자역학에서 각운동량과 스핀은 중요하면서도 알아내어 가는 과정이 상당히 험난합니다. 각운동량은 핵과 전자 사이의 관계 및 전자나 기본 입자와 같은 성질을 파헤치는 영역이기 때문에 양자역학에서 가장 중요한 주제 중 하나이고 그만큼 이해하기도 난해하고, 계산 과정도 복잡합니다.
참고로 각운동량에 대한 분석을 하는 과정은 양자역학 교과서마다 조금씩 차이가 있습니다. 주관적인 생각으론 크게 Griffiths 방식과 Gasiorowicz 방식이 있다고 할 수 있는데, 전자는 약간 Algebric 한 방법으로 직진하고 후자도 비슷하긴 한데 Bracket notation 을 위주로 풀어갑니다. 우선 저는 두 방법을 혼합하긴 할 것인데 전자의 책을 좀 더 참고하도록 하겠습니다.1 그리고 후자의 책 방법에 대해서도 빠지는 내용 없이 추후 포스팅을 할 것이니 걱정하지 않으셔도 됩니다.
1. 각운동량(Angular moment)
1) 고전역학에서의 정의
고전역학에서 '각운동량(Angular moment)'는 회전하는 대상(물체)의 위치벡터와 선운동량의 외적이다.
$$\mathbf{L}=\mathbf{r}\times \mathbf{p}=\begin{vmatrix}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
x &y &z \\
p_x & p_y &p_z
\end{vmatrix}=(yp_z-zp_y)\,\mathbf{i}+(zp_x-xp_z)\,\mathbf{j}+(xp_y-yp_x)\,\mathbf{k}$$
이 개념을 모른다면 양자역학이 아닌 일반물리학을 공부해야 합니다.
2) 양자역학에서의 정의
양자역학에서의 각운동량도 기본적으로 위의 고전적에서의 정의를 따른다. 각 성분을
$$L_x=yp_z-zp_y \\ L_y=zp_x-xp_z \\ L_z=xp_y-yp_x$$ 으로 적고, 다만 여기서 선운동량의 성분들은 연산자에 해당하여
$$p_x=\frac{\hbar}{i}\frac{\partial }{\partial x}\;,\;p_y=\frac{\hbar}{i}\frac{\partial }{\partial y}\;,\;p_z=\frac{\hbar}{i}\frac{\partial }{\partial z}$$ 로 취급한다.
양자역학에서도 각운동량의 정의는 고전역학에서와 같습니다. 그런데 각운동량을 정의한다는 것은 사실 회전이 어떤 상태로 벌어지고 있는지가 먼저 정해져야 합니다. 여기서 회전은 [그림 2]와 같이 전자가 원자핵 주위를 공전하는 것을 말하는 것으로 핵 주위를 돌고 있는 전자의 각운동량을 말하는 것입니다.2 그래서 '궤도 각운동량(Oribital angular momentum)'이라고 부르는 것이 정확합니다. 앞으로 기호 $L$로 표현되는 것은 모두 궤도 각운동량을 뜻하는 것이며 이외에 '스핀 각운동량(Spin angular momentum)'이라는 것도 존재하지만, 그것은 궤도 각운동량에 대한 분석을 모두 마친 뒤에 분석할 것입니다.
2. 각운동량 연산자 사이의 교환 관계
기본적으로 각운동량에 대한 분석은 교환자를 사용하는 것 위주로 진행됩니다. 우선 교환자를 사용한다는 것은 초보적으로 말하면 두 연산자 사이의 관계를 본다는 것이고, 나름 전문적으로 말하면 동시 고유벡터를 찾을 수 있다는 희망을 향해 달려가는 것에 해당합니다.
1) 각운동량 성분들 사이의 교환관계
정리($Q.M$) 4.1
각운동량 성분 $L_x, L_y, L_z$ 사이의 교환관계는 다음과 같다.
$$\left[ L_x,L_y \right]=i\hbar L_z \\ \left[ L_y,L_z \right]=i\hbar L_x \\ \left[ L_z,L_x \right]=i\hbar L_y$$ 순환 관계를 가지므로, 다음과 같이 간단히 표기할 수 있다.
$$\left[ L_i,L_j \right]=i\hbar \,\epsilon_{ijk}L_k$$
증명시 다음의 교환자 관계식을 사용한다.
$$\left[ A-B,C-D \right]=\left[ A,C \right]-\left[ A,D \right]-\left[ B,C \right]+\left[ B,D \right]$$
교환자 식까지 증명하진 않겠습니다. 단순히 양변을 계산하면 맞는지 아닌지 확인할 수 있으니 각자 해보시길 바랍니다.
증명) 열심히 계산하면 된다.
$$\begin{align*}
\left[ L_x,L_y \right]&=\left[ yp_z-zp_y,zp_x-xp_z \right]\\\\&=\left[ yp_z,zp_x \right]
-\left[ yp_z-xp_z \right]-\left[ zp_y,zp_x \right]+\left[ zp_y,xp_z \right]\\\\&=
\left[ yp_z,zp_x \right]+\left[ zp_y,xp_z \right]\\\\&=\left( yp_z\, zp_x-zp_x\,yp_z \right)+
\left( zp_y\,xp_z-xp_z\,zp_y \right)\\\\&=yp_x\left[ p_z,z \right]+xp_y\left[ z,p_z \right]\\\\&=i\hbar \left( xp_y-yp_x \right)\\\\&=i\hbar L_z
\end{align*}$$
사실 뻘짓을 했다고 볼 수 있습니다. 각운동량의 세 성분 $L_x, L_y, L_z$ 중 임의의 둘을 뽑아도 서로 교환하지 않으므로 동시 고유벡터를 뽑을 수가 없기 때문입니다. 3 그래도 교과서들에서는 결국 큰 의미가 없음을 경험적으로 알려주기 위해 이 작업을 거칩니다. 그래서 새로운 계산을 해봅니다.
2) $L^2$ 과 $\mathbf{L}$ 성분의 교환 관계
정리($Q.M$) 4.2
각운동량의 제곱과 각운동량 벡터의 각 성분들은 서로 교환한다.
$$\left[ L^2,L_x \right]= \left[ L^2,L_y \right]= \left[ L^2,L_z \right]=0 \;\;\Leftrightarrow \;\; \left[ L^2,\mathbf{L} \right]=0$$
증명시 다음의 교환자 관계식을 이용한다.
$$\left[ AB,C \right]=A\left[ B,C \right]+\left[ A,C \right]B$$
증명) 각운동량 성분 중 $L_z$ 를 뽑아 (대표로) 계산한다.
$$\begin{align*}
\left[ L^2,L_z \right]&=\left[ L_x^2+L_y^2+L_z^2,L_z \right]=\left[ L_x^2,L_z \right]+\left[ L_y^2,L_x \right]
+\left[ L_z^2,L_z \right]\\\\&=\left[ L_x^2,L_z \right]+\left[ L_y^2,L_x \right]
\\\\&=L_x\left[L_x,L_x \right]+\left[ L_x,L_z \right]L_x+L_y\left[ L_y,L_z \right]+\left[ L_y,L_z \right]L_y
\\\\&= -i\hbar L_xL_y-i\hbar L_yL_x+i\hbar L_yL_x+i\hbar L_xL_y \\\\&=0
\end{align*}$$
같은 방법으로 $L_x,L_y$ 를 각각 $L^2$ 와 교환자 계산을 수행하여도 $0$ 을 얻게 된다.
3. 각운동량 사다리 연산자(Ladder operation of angular moment)
이제 교환관계 $\left[ L^2,L_z \right]$ 를 바탕으로 고유값 방정식을 다음과 같이 두 개 세웁니다.
$$\left\{ \begin{array}{cl}
\;L^2|\,l,m\rangle=\lambda|\,l,m\rangle \;\;\;\;\;\cdots \;\;\;(1)\\\\
\;L_z|\,l,m\rangle=\mu|\,l,m\rangle\;\;\;\;\;\cdots \;\;\;(2)
\end{array} \right.$$
두 고유값 $\mu, \lambda$ 는 상수배 차이만 나게 됩니다. 그리고 고유벡터는 켓벡터로 $|\,l,m\rangle$ 라 적었습니다. 원래 브라켓 표기법으로 켓벡터를 쓰고 싶다면 그냥 $|\psi\rangle$ 라고 적으면 되는데, 굳이 이렇게 쓰는 이유는 $\psi$ 가 결과적으로 $l,m$ 의 함수가 되기 때문입니다. 그리니 수학적 관점에선 $\psi_l^m$ 으로 써도 상관은 없습니다만 양자역학이니 디랙 표기법을 사용하는 것입니다. 뒤에서 다시 다루겠지만 $l$은 궤도 양자수이고 $m$은 자기 양자수에 해당합니다.
이 고유값 방정식을 다루기 위해, 조화 진동자에서처럼 사다리 연산자를 도입합니다.
각운동량에 관한 사다리 연산자를 다음과 같이 정의한다.
$$L_{\pm}:=L_x\pm iL_y$$
사다리 연산자를 $L_z, L^2$ 와 각각 교환시켜 봅시다.
$$\begin{align*}
\left[ L_z,L_{\pm} \right]&=\left[ L_z,L_x\pm iL_y \right]=\left[ L_z,L_x \right]\pm i\left[ L_z,L_y \right]
\\\\&=i\hbar L_y\pm i(-i\hbar L_x)\\\\&= \pm \hbar \left( L_x\pm iL_y \right)= \pm \hbar L_{\pm}\;\;\;\;\;\cdots \;\;\;(3)
\end{align*}$$
$$\begin{align*}
\left[ L^2,L_{\pm} \right]&=\left[ L^2, L_x\pm iL_y \right]\\\\&=\left[ L^2, L_x \right]\pm i\left[ L^2,L_y \right]=0\;\;\;\;\;\cdots \;\;\;(4)
\end{align*}$$
교환자는 값이 0이 될 때 신나야 합니다. 누차 말하지만 교환했을 때 0이 되어 교환 가능하면 동시 고유벡터를 갖습니다. $L_z$ 의 경우 직접 사다리 연산자와 교환하진 않는데 $L^2$ 는 사다리 연산자랑 교환하네요. 이로부터 몇가지 재밌는 사실을 알 수 있게 됩니다.
정리($Q.M$) 4.3
식 $(4)$ 에 의하여
$$L^2(L_{\pm}|\,l,m\rangle)=L_{\pm}\left( L^2|\,l,m\rangle \right)=L_{\pm}\left( \lambda |\,l,m\rangle \right)
=\lambda\left( L_{\pm}|\,l,m\rangle \right)$$ 가 성립한다. 즉, $|\,l,m\rangle$ 뿐만 아니라 $L_{\pm}|\,l,m\rangle$ 또한 $L^2, L_z$ 의 고유벡터이다.
정리($Q.M$) 4.4
식 $(3)$에 의하면 $L_{\pm}$는 $L_z$와 교환하진 않지만,
$$\begin{align*}
L_zL_{\pm}|\,l,m\rangle&=\left( L_zL_{\pm}-L_{\pm}L_z \right) |\,l,m\rangle +
L_{\pm}L_z|\,l,m\rangle \\\\&=\pm\hbar L_{\pm}|\,l,m\rangle+L_{\pm}\left( \mu|\,l,m\rangle \right)
\\\\&= \left( \mu\pm\hbar \right)\,L_{\pm}|\,l,m\rangle
\end{align*}$$ 와 같이 계산하면 $L_{\pm}|\,l,m\rangle$ 은 새로운 고유값 $(\mu\pm\hbar )$ 를 갖는 $L_z$ 의 고유벡터이다.
두 정리의 결론은 매우 매우 중요합니다. 이를 이해하면 왜 $L_{\pm}$ 가 정확히 사다리 연산자인지를 깨닫게 됩니다. 이 연산자는 $L^2, L_z$ 의 고유벡터이면서 동시에 고유값을 한 칸(=$\hbar$) 씩 내리거나 올리는 역할을 하기 때문이죠. 위의 두 정리를 결합하여 아래의 정리, 즉 사다리 연산자의 의의를 획득할 수 있습니다.
정리($Q.M$) 4.5
$L_{+}$ 는 '올림 연산자(Rasing operator)' 또는 '생성 연산자(Creation operator)' 라 부른다. 그 까닭은 $L_z$ 의 고유값을 $\hbar$ 만큼 증가시키기 때문이다.
$L_{-}$ 는 '내림 연산자(Lowering operator)' 또는 '소멸 연산자(Annihilation operator)' 이라 부른다. 그 까닭은 $L_z$ 의 고유값을 $\hbar$ 만큼 감소시키기 때문이다.
여기서 고유값 방정식은
$$L_z\left[ L_{\pm}|\,l,m\rangle \right]=\left( \mu\pm\hbar \right)\left[ L_{\pm}|\,l,m\rangle \right]$$ 임에 주의하라.
주의깊게 기억해야 할 것이 있는데, 사다리 연산자가 고유벡터에 적용되는 것이 아닙니다. 위 박스 마지막에 적어두었듯이 고유값 방정식에서 연산자는 $L_z$ 이고 고유벡터는 $L_{\pm}|\,l,m\rangle$ 입니다. 즉 이 방정식에서 고유벡터는 $|\,l,m\rangle$ 이 아니고 $L_{\pm}|\,l,m\rangle$ 이라는 것입니다. 그래서 위 정리에서 주어와 목적어, 수식어를 똑바로 읽어낼 줄 알아야 합니다.
4. 고유값의 최대·최소
그러나 사다리 연산자로 고유값을 무한정 내리거나 무한정 올릴 수는 없기에 상한과 하한을 결정해야 합니다.
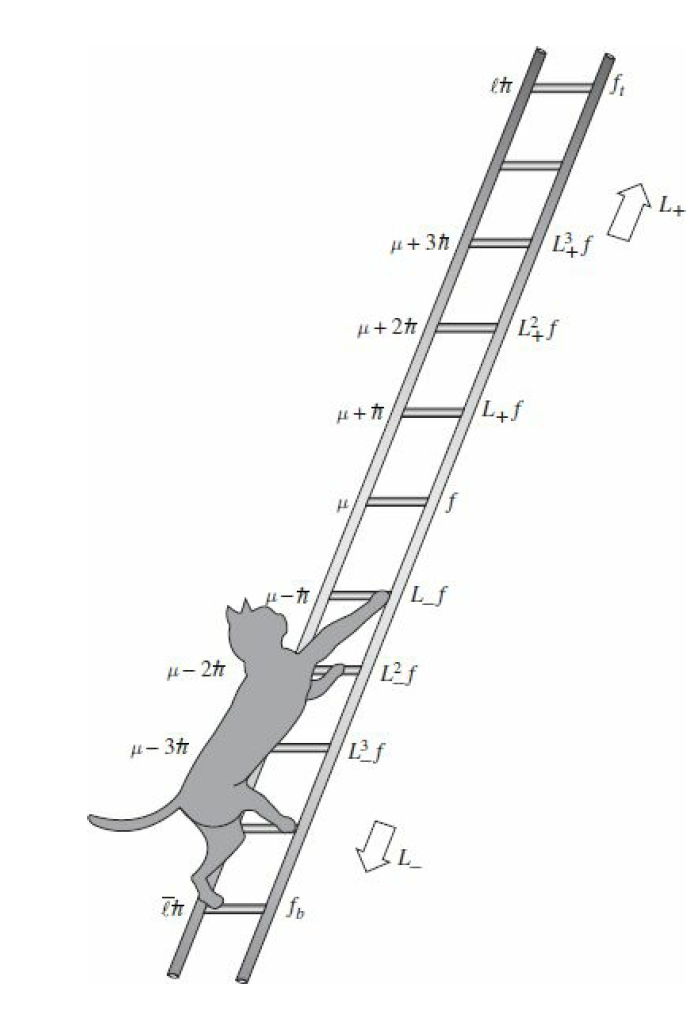
1) 상한 정하기
가장 높은 고유값을 $l$, 고유벡터는 $|\,l,m\rangle_t$ 라 하겠습니다.4 첨자 $t$ 는 가장 높다는 뜻에서 top 을 의미하는 것입니다. 그러면 고유값 방정식은
$$\left\{ \begin{array}{cl}
\;L_+|\,l,m\rangle_t=0 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\cdots \;\;\;(5) \\\\
\;L_z|\,l,m\rangle_t=(l\hbar)|\,l,m\rangle_t\;\;\;\;\cdots \;\;\;(6) \\\\
\;L^2|\,l,m\rangle_t=\lambda |\,l,m\rangle_t\;\;\;\;\;\;\;\cdots \;\;\;(7)
\end{array} \right.$$
우선, 첫째 식은 $|\,l,m\rangle_t$ 에선 한번 더 올림 연산자를 적용할 경우 상한이기에 0이 된다는 뜻입니다. 둘째 식은 상한 고유벡터 $|\,l,m\rangle_t$ 에 대해선 고유값이 $l\hbar$ 임을 뜻합니다. 셋째 식은 원래 맨 처음에 세웠던 고유값 방정식이죠.5
목적은 이 셋을 적절히 비벼서 $\lambda$ 와 $l$의 관계를 찾는 것입니다. 이 작업을 하려면 또 귀찮은 계산을 해야만 합니다. 우선 사다리 연산자 두 개를 연달아 곱해봅시다.
$$\begin{align*}
L_{\pm}L_{\mp}&=(L_x\pm iL_y)(L_x\mp iL_y)\\\\&=L_x^2+L_y^2 \mp i\left( L_xL_y-L_yL_x \right)
\\\\&= (L^2-L_z^2)\mp i\left[ L_x,L_y \right]\\\\&=
L^2-L_z^2\mp i(i\hbar L_z)\\\\&= L^2-L_z^2\pm \hbar L_z
\end{align*}$$
이로부터 깔끔히 정리된 식 4개를 뽑아낼 수 있습니다. 네 식은 결국 다 같은 식입니다.
정리($Q.M$) 4.6
사다리 연산자, 각운동량 제곱, 각운동량의 성분 셋을 연결하는 식은 다음과 같다.
$$L^2=L_{\pm}L_{\mp}+L_z^2\mp \hbar L_z\\\\\\
L_+L_-=L^2-L_z^2+\hbar L_z\\\\\\
L_-L_+=L^2-L_z^2-\hbar L_z\\\\\\
L^2=\frac{1}{2}\left( L_+L_-+L_-L_+ \right)L_z^2$$
그러면
$$\begin{align*}
L^2|\,l,m\rangle_t&=\lambda |\,l,m\rangle_t=\left( L_-L_++L_z^2+\hbar L_z \right)|\,l,m\rangle_t
\\\\&=\left( 0+\hbar^2l^2+\hbar^2l \right)|\,l,m\rangle_t
\\\\&= \hbar^2 l(l+1)|\,l,m\rangle_t
\end{align*}$$
드디어 $\lambda=\hbar^2l(l+1)$ 의 관계를 알아냈네요.
2) 하한 정하기
하한도 정해야 합니다. 속도를 좀 내보죠.
$$\left\{ \begin{array}{cl}
\;L_-|\,l,m\rangle_b=0 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\cdots \;\;\;(8) \\\\
\;L_z|\,l,m\rangle_b=(\bar{l}\hbar)|\,l,m\rangle_b\;\;\;\;\cdots \;\;\;(9) \\\\
\;L^2|\,l,m\rangle_b=\lambda |\,l,m\rangle_b\;\;\;\;\;\;\;\cdots \;\;\;(10)
\end{array} \right.$$
달라진 것은 최소 고유값을 $\bar{l}\hbar$ 로 표기한 것과 고유벡터의 첨자를 바닥을 뜻하는 bottom 의 첨차 b를 달았다는 것입니다.
$$\begin{align*}
L^2|\,l,m\rangle_b&=\left( L_+L_-+L_z^2-\hbar L_z \right)|\,l,m\rangle_b
\\\\&=\left( 0+\hbar^2\bar{l}^2-\hbar^2\bar{l} \right)|\,l,m\rangle_b
\\\\&=\hbar^2\bar{l}^2(\bar{l}-1)|\,l,m\rangle_b
\end{align*}$$
여기서는 $\lambda=\hbar^2\bar{l}^2(\bar{l}-1)$ 를 얻을 수 있네요.
3) 고유값 $\lambda$ 는?
이쯤 적으니까 글이 너무 길어서 렉이 걸리고 있습니다. 1)과 2)에서 얻은 $\lambda$ 값이 같아야 합니다.
$$l(l+1)=\bar{l}(\bar{l}-1) \;\;\Rightarrow \;\; l=-\bar{l}\;\;\;\mathrm{or}\;\;\; \bar{l}=l+1$$
그러나 $\bar{l}=l+1$ 의 경우 최소 고유값이 최대 고유값보다 크다는 모순이 나오므로 우리가 선택할 해는
$$\bar{l}=-l$$
이 됩니다. 즉 고유값의 범위가 $-l$ 부터 $+l$ 까지라는 것입니다! 그리고 올림 연산자와 내림 연산자는 각각 고유값을 정확히 $\hbar$ 만큼, 다시 말해 사다리 연산자를 여러번 작용하더라도 $\hbar$ 의 정수배만큼만 변하게 됩니다. 이제 마무리를 해봅시다.
정리($Q.M$) 4.7
각운동량에 관한 고유값 방정식은
$$ \left\{ \begin{array}{cl}
L^2|\,l,m\rangle=\hbar^2l(l+1)|\,l,m\rangle \\\\
L_z|\,l,m\rangle=m\hbar |\,l,m\rangle
\end{array} \right.$$
로 정리할 수 있다. 이 때 $-l\le m \le +l$ 이며 각 $m$값은 정수만큼의 차이가 나게 된다. 또한 여기서 사다리 연산자로 고유값은 $\hbar$ 의 정수배만큼씩 올라갈 수 있어서, 최대 고유값과 최소 고유값의 차는 자연수가 되어야 한다. 이 경우, $l$ 은 정수거나 반정수(정수의 절반)이 될 수 있다.
정리($Q.M$) 4.8
$l$ 이 정수가 되는 경우,6 $l$을 '궤도 주양자수(Orbital quantum number)'이라 부른다.
$l$ 이 반정수가 되는 경우, 관례적으로 $s$ 로 표기하며, '스핀 양자수(Spin quantum number)' 이라 부른다.
$m$ 값은 '자기 양자수(Magnetic quantum number)' 이라 부른다. $m=-l,-l+1,\cdots ,l-1,l$ 의 값들이 존재한다. $m$ 값은 구면조화함수에서 방위각 주기성을 만족하는 물리적인 의미를 가지기 위해 정수여야만 한다.
고유값 방정식을 깔끔히 정리했지만, 숙제가 남습니다. 바로 $l$ 값이 반정수인 경우, 스핀에 대한 해결법을 찾지 못했다는 것입니다. 우리가 지금 계산한 과정 - 청록색 두 박스를 제외한 모든 내용들 - 은 각운동량의 정의 자체를 제외하면 순수 '수학'이지 물리가 아닙니다. 다시 말해 철저히 선형대수학의 언어로 수학적 논리를 밟아 계산을 했을 뿐입니다. 물리학이 되려면 마지막에 나온 결과에 의미를 부여해주어야 합니다. 즉 수학적으로 $l$ 값은 반정수가 될 수 있으나, 물리적으로 보면 $l$ 이 반정수가 될 경우 $m$ 값도 정수가 아닌 반정수가 될 수 있다는 말인데, 고유벡터 $|\,l,m\rangle$ 를 $\theta, \phi$ 에 관하여 3차원 구면좌표계에서 전개할 경우 고유벡터 $|\,l,m\rangle$ 는 구면조화함수(Spherical harmonic function)에 대응되는데 물리학적으로 방위각 주기성이 만족되어야 하므로 $m$은 반정수가 될 수 없습니다.
그렇다면 대수적으로 $l$ 은 반정수가 될 수 있으나 물리적으로 $l$ 이 반정수가 되는 경우를 제외해야 할까요? 수학은 우주의 언어이기 때문에 수학적 개념에 대응되는 자연의 물리적 성질이 존재한다는 명제는 여기서도 깨지지 않습니다. $l$ 이 반정수인 경우에 대응되는 자연의 비밀스런 성질은 기본입자의 고유 성질이라 알려져 있는 스핀이라는 녀석입니다. 스핀은 각운동량의 성질을 대부분 물려받으면서도 약간의 독특한 성질을 가지고, 양자역학에서 매우 흥미로운 주제입니다. 수학과 물리의 조화는 양자역학에서도 여전히 강력하게 유지된다는 것입니다.
[참고문헌]
Introduction to Quantum mechanics, David Griffiths, 3e
Quantum physics, Stephen Gasiorowicz, 3e
- 사실 Gasiorowicz 는 원래 설명이 대충 되어 있는 것으로 악명 높습니다. 그렇지만 알짜배기 내용들을 정확히 포함하고 있기 때문에 제 블로그의 양자역학 글들에선 Gasiorowicz 를 더 많이 참고했었습니다. 다만 Griffiths 책의 연습문제를 보면 Gasiorowicz 에서 다루는 방법들이 포함되어 있으니 적당한 책을 골라 공부하시면 됩니다. [본문으로]
- 물론, 전자는 구름 모형으로 해석하는 것이 맞기에 실제 이 [그림 2]처럼 정확히 위치를 알고 있는 것처럼 보이는 그림은 완벽하진 않으며, 어떤 위치에서 정확히 공전하고 있는지를 관측할 수는 없습니다. 하지만 우리가 정확히 전자를 관측할 수 있는지에 관한 논의를 떠나서, 어찌되었든 전자는 핵 주위를 공전하고 있기에, 궤도 각운동량을 다루는 데에는 문제가 없습니다. [본문으로]
- 동시 고유벡터 포스팅을 반드시 참고하시기 바랍니다. Griffiths 교재에서는 이를 설명하지 않고 대신 불확정성 정리를 소개하여 넘어가는데, 그보다는 동시 고유벡터 개념을 알고 있는 것이 좋습니다. [본문으로]
- 고유값을 $l$ 로 적으면 문자가 중복되서 의미가 흐려질 수 있다고 생각할 수 있지만, 고유벡터에 들어있는 $l$ 값이 가장 높은 고유값에 해당함이 밝혀질 것이기에 같은 문자로 씁니다. 하지만 이러한 의문은 사실 허점이 있는데, 어디까지나 아직 고유벡터에서 우리가 쓰고 있는 $l$ 의 의미는 밝혀지지 않은 상태라는 것을 기억합시다. [본문으로]
- 벌써 까먹으셨다면, 이 포스팅의 3번 도입부로 쭉 올라가 보세요. [본문으로]
- 아직까지 $l$ 에 물리적 의미를 부여하지 않았습니다. 즉 이름을 붙이지 않았다는 겁니다. 즉 아직까지 $l$ 은 그냥 미지수입니다. [본문으로]
'양자역학(Quantum Physics) > 3차원 문제' 카테고리의 다른 글
| 3차원 슈뢰딩거 방정식 (3-dimension Schrodinger equation) (0) | 2022.06.11 |
|---|
댓글