일차결합, 일차독립, 일차종속의 개념을 이해했다면 공간을 이루는 기초 요소 벡터인 기저에 대한 개념을 확립할 수 있습니다. 기저는 어떤 공간을 형성하기 위한 기본 재료라고 할 수 있어서, 공간의 차원을 결정하는 중대한 도구입니다. 선형대수학에서 등장하는 많은 기저와 공간은 서로 밀접한 연관성을 가집니다. (유클리드 공간,내적공간, 직교공간...) 고등학교 수학에서 벡터 표현을 $(3,2,4)$로 하였다면 대학 미적분학에서는 이보다는 $3\mathbf{i}+2\mathbf{j}+4\mathbf{k}$ 로 하게 되는데, 이것이 기저를 적극적으로 활용하는 대표적인 예입니다. 어렵지 않은 내용이니 부담 없이 본론으로 들어가 보도록 합시다.
1. 기저(Basis)
기저가 될 조건은 일차독립이면서 벡터공간 $V$를 생성해야 한다는 것입니다. 벡터공간 $V$의 임의의 원소를 가리키는 벡터를 항상 선형결합으로 만들 수 있어야 합니다. 그러니 일차종속인 벡터들로 이루어진 집합에서 어떤 벡터공간을 만든다면 그 집합 자체로는 기저가 될 수 없습니다. (종속인 벡터가 $n$개라면, $n-1$개의 벡터를 제거하면 기저가 될 것입니다)
일차종속과 독립에 관한 글에서 벡터를 늘리거나 줄여서 다른 벡터를 만들 수 있는지에 관한 설명을 한 적이 있습니다. 만약 하나의 벡터를 가지고 있고 그것의 스칼라 배를 해서 만들 수 있는 임의의 벡터에 대해 두 벡터는 일차종속이라고 설명한 적이 있지요. 임의의 한 벡터만을 가지고 있을 때는, 그것을 선형결합 해도 생성할 수 있는 도형이 직선 뿐입니다. 그렇다면 어떤 직선 위의 점들이 벡터공간이라고 한다면 그 직선은 기저벡터 1개로 생성된 공간입니다. 이런 공간을 '1차원'이라고 하지요. (차원의 자세한 정의는 후술)
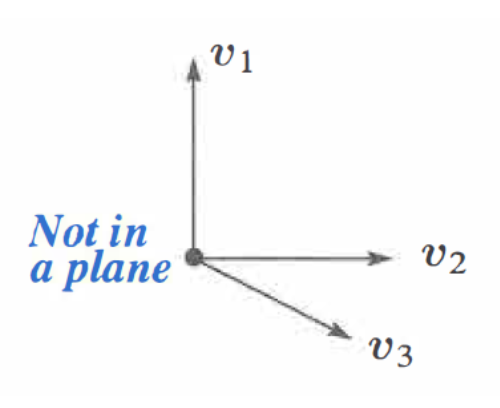
그렇다면 독립인 벡터 2개를 가지고 있을 때는 어떠할까요? 그 두 벡터를 선형결합했을 때 어떤 평면 하나를 얻게 될 것입니다. 그 평면이 벡터공간이라면 이 두 벡터는 평면의 기저에 해당하게 됩니다. 3차원 공간이면 위 그림처럼 세 기저는 한 평면에 존재할 수 없으며, 일차독립이어야 합니다. 우리가 사용하는 $x,y,z$축 방향의 임의의 벡터 세개를 고르면 3차원 실수 공간의 기저가 됩니다.
2. 기저가 가지는 여러가지 특징들
일반적으로 $n$차원 공간을 만드려면 $n$개의 기저가 필요합니다. 기저를 가지고 있으면 벡터공간을 만들 수 있으며, 역으로 벡터공간이 존재한다면 그것의 기저가 반드시 존재하고 찾을 수 있습니다.
1) 한 벡터공간의 기저의 개수는 무수히 많다.
기저에 관한 몇가지 특징이 존재하는데, 그 중 하나는 한 벡터공간의 기저의 개수가 매우 많을 수 있다는 것입니다. 예컨대 실수 전체 평면 R^2의 기저는 몇가지가 존재할까요? 그 답은 간단히 평면상에서 일차독립인 두 벡터를 고르면 끝납니다. 두 벡터는 선형결합하여 실수 평면을 만들 수 있기 때문이지요. 몇가지를 구해보면
$$\left \{ (1,1),(-2,0) \right \}\;,\;\left \{ (-1,0),(0,-3) \right \}$$
등이 있습니다. 이들 모두 2차원 실수 평면의 기저에 해당합니다. 이로부터 임의의 기저를 뽑았을 때 그 벡터공간 전부를 나타낼 수 있기 때문에, 내가 뽑은 기저로 다른 무수히 많은 기저들 또한 생성할 수 있습니다. 즉 벡터공간의 한 기저는 그 벡터공간의 기저를 형성합니다.
2) 순서기저
기저로 구성된 집합의 원소인 기저들에 순서를 부여한 것을 말합니다. 보통 집합에서 $\left \{ a,b,c \right \}\;,\;\left \{ c,b,a \right \}$ 는 같은 집합으로 취급합니다. 그렇지만 순서기저라는 것은 둘을 다르게 보겠다는 것입니다. 이 순서를 매기는 것이 뭐가 중요할까, 의문이 들 수 있는데 우리가 $3\mathrm{e_1}+2\mathrm{e_2}-\mathrm{e_3}$ 라고 썼다고 해봅시다. 엄밀하게는 $1\leq i\leq 3$에 대하여 $\mathrm{e_i}$이 순서기저라고 해야 저 벡터가 $(3,2,-1)$이라고 할 수 있습니다. 만약 저 세 $\mathrm{e_i}$가 $x,y,z$ 순서가 아니라고 할 수도 있기 때문입니다.
3) 표준 기저(Standard basis)
이렇게 한 벡터공간의 기저가 무수히 많을 수 있어서 사람들이 통용할 수 있는 가장 간편한 기저를 정했는데 그것을 표준기저라고 하고 우리가 줄곧 사용해왔던 것입니다. 표준기저란 $\mathrm{e_1},\mathrm{e_2},\mathrm{e_3}$ ... 또는 $\mathbf{i},\mathbf{j},\mathbf{k}$ 등으로 나타내는 벡터를 말하며, n차원 (유클리드) 공간에서 n개의 서로 독립인 벡터들이 모두 수직관계를 이루고 있는 것을 말합니다. 쉽게 생각하면 2차원, 3차원의 $x,y,z$축을 떠올리면 됩니다. 이들은 서로 수직이라 독립인 것이 자명하고 그 방향으로의 크기가 1인 단위벡터가 표준기저에 해당합니다. 이 때 $x,y,z$축 방향에 대해 각각 첨자로 1,2,3 과 i,j,k 를 사용하는 것이 일반적이기 때문에 우리는 기본적으로 '표준순서기저(Standard ordered basis)'를 사용합니다.
벡터공간 $F^n$에서 $i$번째 성분만 1이고 나머지 성분은 모두 0인 벡터를 $\mathrm{e_1}$ 로 나타낸다. $\mathrm{e_1}$ 들로만 구성된 집합을 '표준기저(standard basis)'라 하고, 특히 집합 $\left \{ \mathrm{e_1},\mathrm{e_2},\cdots ,\mathrm{e_n} \right \}$ 를 '표준순서기저(Standard ordered basis)'라 한다.
예를 하나 들어봅시다. 임의의 2차 다항식의 집합을 $P_2(x)$라고 씁니다. $P_2(x)$ 의 표준순서기저는 $\left \{ 1,x,x^2\right \}$ 가 됩니다. 이들을 기저로 삼아 앞에 적절한 스칼라를 붙이면 세상에 존재하는 모든 2차 다항식을 나타낼 수 있기 때문입니다.
3) 기저에 관한 정리
다음 정리는 기저의 성질을 완벽히 보여주면서, 기저가 될 필요충분조건을 설명하고 있습니다.
벡터공간 $V$의 기저 $\beta$가 $n\in N$개의 벡터로 이루어져 있을 때, $n$은 $V$의 '차원(dimension)'이라 하며 $\mathrm{dim}(V)$로 나타낸다. 이 때 $n$은 유일하고 이 차원은 '유한차원(finite dimension)'이라 한다. 유한차원이 아닌 벡터공간의 차원은 '무한차원(infinite dimension)'이라 한다.
기저를 이용해 공간의 한 점을 나타내는 방법은 유일해야 한다는 것입니다. 기저의 성질에 의하면 2차원 공간에서 어떤 벡터 두 개를 가지고 앞에 적당한 숫자를 붙여 선형결합 했을 때 임의의 벡터를 나타낼 수 있어야 하는데, 한 점을 나타내는 두 가지 선형결합이 존재할 수는 없습니다. 그리하여 벡터의 표현 방법이 유일해야 기저로 취급할 수 있다는 것입니다.
3. 차원(Dimension)
학부 수준의 선형대수학에서는 대부분 유한차원을 다룹니다. 우리가 알고 있는 실수 평면, 공간은 차원이 한정되어있는 유한차원입니다.
무한차원의 경우, 대표적으로 양자역학에서 등장하는 힐베르트 공간이 있는데 그 이유는 파동함수의 성질 때문입니다. 다만 이건 너무 어려운 이야기니까 간단한 무한차원을 생각해봅시다. 체(field)를 원소로 하는 다항식의 차원은, 기저의 원소 개수가 무한히 많기 때문에, 즉 기저가 $\left \{ 1,x,x^2,\cdots \right \}$ 로 끝을 정할 수 없겠지요? 그러므로
$$\mathrm{dim}(P(F))=\infty$$
가 됩니다.
'선형대수학(Linear Algebra) > 벡터공간' 카테고리의 다른 글
| 벡터의 선형독립과 선형종속 그림으로 이해하기 (Linearly independent, Linearly dependent) (0) | 2020.12.13 |
|---|---|
| 벡터의 선형결합, 일차결합 (Linear Combination) (2) | 2020.12.13 |
| 벡터공간의 부분공간 (Subspace) (1) | 2020.12.11 |
| 벡터공간의 정의 (Vector space) (6) | 2020.12.11 |


댓글