도체, 반도체, 부도체는 물질을 전기 전도성에 따라 분류한 것이라 할 수 있습니다. 반도체는 2021년 현재에도 호황이며, 나아가 차세대에도 꾸준히 각광받을 기업의 강력한 기술이자, 보배입니다. 그러나 아쉽게도, 반도체의 과학적 원리를 정확히 이해하기 위해서는 전자기학을 넘어 양자역학이 필요합니다. 반도체를 배우기 위해서는 도체와 부도체(절연체)에 대한 이해가 필요한데, 그 중 가장 간단해서 먼저 배우는 것이 바로 도체입니다.
도체와 이것의 전기 전도성에 대해서는 그다지 열심히 설명하지 않더라도 이 글을 보고 계신 분들이라면 대략적으로 알 것이라 생각합니다. 도체는 기본적으로 열 및 전기 전도성이 뛰어나고, 원자 내부에만 속박되어 있지 않은 자유전자가 존재하며, 원자가 띠의 일부가 비어있어 이 공간에서 전자가 자유롭게 이동할 수 있습니다.
이렇게만 보면 도체는 간단히 전기가 잘 통하는 물질이라 생각할 수 있는데, 이렇게만 생각하면 몇가지 오해를 불러 일으킬 수 있습니다. 그렇다면 우리가 배우고 있는 전기장이나 전위의 개념을 사용했을 땐 도체를 어떻게 설명할 수 있는지, 그리고 특히 도체 내부에서는 어떤 일이 벌어지는지를 알아봅시다. 결론부터 말하자면 번개가 쳤을 때 자동차 내부에 있는 사람은 안전하다는 말이 있는 것처럼, 도체 내부에는 전기가 통하지 않습니다.
1. 도체의 기본성질
1) 도체 내부에서 전기장은 0이다.
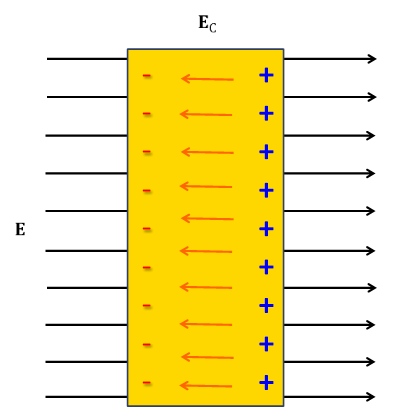
① 외부 전기장이 존재하는 경우 & 전기적 중성 도체
우선, 도체 내부에 알짜 전하가 없어서 전기적으로는 음전하와 양전하의 전하량이 같아 중성인 상태를 고려해봅시다. [그림 1]과 같이 외부에 전기장 $\mathbf{E}$ 가 존재할 때 그 속에 도체(노란색 직사각형)을 놓아 두었습니다. 도체 내부에는 자유전자가 존재하기 때문에, 외부 전기장에 반응하여 자유전자들이 이동해서 새로운 전기장 $E_C$ 가 도체 내부에 생성됩니다. 이렇게 외부 전기장에 의해 유도된 전하들을 유도전하(Induced charge)라 하며 원래 있는 장 $\mathbf{E}$ 를 지우는 역할을 합니다. 결국 $\mathbf{E}=\mathbf{E}_C$ 가 될 때까지 자유전자가 이동하여 알짜 전기장이 완전히 사라지게 되어, 도체 내부의 전기장은 0이 됩니다. 그리고 이러한 일들은 순식간에 발생하게 됩니다.
$$\mathbf{E}_{\mathrm{Inside}}=\mathbf{E}+\mathbf{E}_C$$

여기서 들 수 있는 의문은 두 가지 정도 있습니다.
첫째, 도체 왼쪽과 오른쪽에 각각 모인 전하들끼리의 반발력을 고려해야 하지 않느냐에 관한 것입니다. 도체 내에 전자 배열은 외부 전기장이 충분히 도체 내부의 같은 종류 전하들끼리의 반발력보다 강한 힘으로 유도를 시켰을 때만 저렇게 그림과 같이 발생합 다. 그렇다면 외부 전기장이 없을 때는 저렇게 유도되지 않을까요? 네, 저렇게 유도되지 않습니다. 그런데 그 상황은 별 중요하지 않다는 것을 아래의 ③에서 다룹니다.
둘째, 도체 내에 외부 전기장을 상쇄시킬만큼의 충분한 자유전자가 존재한다고 단정할 수 있느냐인 것입니다. 원자의 크기는 매우 작고 도체 내부의 자유전자의 개수는 사실 일상생활에서 우리가 만나는 눈에 볼 수 있는 크기의 도체라면 - 그리고 그 내부의 크기를 따질 수 있을 만한 적당한 크기라면 (예컨대 모래알이나 머리카락 굵기의 도체 전선 따위가 있을 때 그것의 내부를 따지는 것은 딱히 큰 의미가 없을 것임) - 전자의 개수는 충분히 많다고 할 수 있습니다. 즉, 적당한 부피를 가진 크기의 도체는 항상 외부 전기장을 상쇄시킬 만큼의 충분한 전자를 매우 많이 보유하고 있습니다. 물론, 이론적으로 외부 전기장을 무한히 늘린다면 언젠가는 평형을 이루지 못할 것이라 예상할 수는 있으나, 자연이 보여주는 대게의 특징은 그러한 일들이 발생하지 않는다는 것이니 깊게 고려하지 않아도 된다는 것입니다.

* 그럼에도 불구하고 도체 내부의 전자의 개수는 정확히 말해서 무한개라고 할 수는 없겠죠? 유한한 부피와 형태를 가지고 있으니 전자의 개수가 아주 많기야 하겠지만 유한하기는 할 것입니다. 그래서 그 전자들을 모두 표면으로도 유도하고도 남을 만큼의 강력한 외부 전기장이 존재하는 경우, 도체는 스파크가 일거나, 폭발하여 파괴됩니다. 이는 유전강도를 넘어서는 파괴 현상과도 유사한데, 이 때 여러가지 방전(discharge)현상이 발생합니다. (ex 코로나 방전) 그러나 일상 생활에서 우리가 탑승할 정도의 크기의 물체가 이렇게 강력한 전기장에 노출되기는 참으로 어렵습니다. 그러므로 일상 생활에서는 아주 거대한 고전압 전류가 흐르는 송전탑, 지하철 전선 등에 다가가지 않는다면 감전되어 죽거나 도체가 파괴되는 현상을 볼 일은 없다고 마무리 지을 수 있겠네요.
② 외부 전기장이 존재하는 경우 & 전기적으로 중성이 아닌 대전된 도체
다만, 우리는 전기적 중성인 도체만 고려했습니다. 만약 저 도체가 대전되어 알짜 전하를 가진 경우에도 내부의 전기장이 0이 될까요? 정답은 '그렇다'라는 겁니다. 만약 저 상황에서 도체 내부 정중앙에 내가 자유전자를 한 움큼 집어서 떨어뜨렸다고 합시다. 그러면 그 즉시 전자들은 도체의 왼쪽 끝단으로 움직입니다. 여전히 외부 전기장의 힘을 받고 있기 때문이죠.
만약 '외부 전기장이 엄청 약한데 알짜 전하는 엄청 많이 퍼부어서 이들이 모두 다 외부 전기장에 의해 끝에 모이지 않으면 어떻게 하나요?' 라는 의문이 든다면 아래의 ④를 읽으시면 됩니다. 간단히 말하면 그 전하들끼리의 반발력 때문에 결국 또 표면에만 남습니다.

이것이 의미하는 바는, 외부 전기장이 있는 한 도체 내부에는 알짜 전하가 존재할 수 없다는 것입니다. 그 알짜 전하들이 죄다 표면으로 도망갑니다. 왜냐하면 내가 도체 내부에 전하를 추가시키는 순간, 그 전하는 그 도체를 지배하고 있는 내부 전기장의 힘을 받지 않을 수가 없고, 따라서 그로 인해 재배열을 받아 도체의 양 끝으로 몰리게 되기 때문입니다. 양전하야 움직일 수 없지만 자유전자는 외부 전기장의 (+)방향으로 밀려나서 도체 왼쪽의 겉표면에 모이게 됩니다.
이와 같은 이유로, 도체에 외부 전기장을 걸어주는 경우 즉 도체에 전기력을 작용한다거나, 전류를 흘려주는 경우 표면에서만 그 효과를 느낄 수 있고 내부에서는 느낄 수 없습니다. 자동차가 번개에 내리치면 전류는 자동차의 겉표면을 따라 지표로 이어져 흐를 뿐, 자동차를 뚫고 내부에 타고 있는 사람이 감전되지는 않습니다. (물론 불이 나서 폭발할 가능성이 높기 때문에 가능한 한 차를 탈출하는게 좋기는 합니다) 항공기 또한 번개를 맞아도 추락하거나 하지 않게 잘 설계되어 있는데 그 조건 중 하나가 표면을 알루미늄 등 도체로 만드는 것입니다. 이 원리를 이용하면 도체로 된 그물을 여러번 감아 외부의 전자기파를 차단할 수 있는데, 이를 흔히 '패러데이 새장'이라고 합니다. 엘레베이터를 탔을 때 전자파 신호가 먹통이 되며 통화가 잘 되지 않는 과학적 원리가 바로 이것입니다. (다만 빛을 막는 전자기 차폐는 단순 전기장을 막는 것보다는 복잡한 원리가 숨어 있습니다. 자기장도 막아야 하니..)
③ 외부 전기장이 존재하지 않는 경우 & 전기적 중성인 도체

가장 일반적인 일상생활에서 우리가 마주하는 도체들의 모습입니다.
외부 전기장도 없는 중성 도체의 경우, 사실 도체 내부 전기장은 당연히 0이며 이를 따지는 것이 딱히 의미가 없습니다. 도체든, 부도체든, 반도체든, 외부에서 전류를 흘러 보내주지 않으면 절대로 스스로 전류가 갑자기 막 흐르지 않습니다. 우리가 밥을 먹으려고 쇠숟가락, 쇠젓가락을 들었는데 갑자기 수저에서 전기가 통해 움찔하거나, 국자를 들다 감전되거나 하지는 않지요. 고의로 도체에 전기장을 가하지 않으면 도체 스스로 전기가 갑자기 흐를 일은 전혀 없습니다. 왜냐하면 자유전자는 무질서하게 도체 내부에서 이동하고 있는데 전류라는 것은 전하들이 한 방향으로 시간에 따라 일정한 속도로 움직인다는 것이거든요. 이건 마치 공기 중의 공기 분자들이 갑자기 한 시점에 줄을 지어 직선으로 움직인다는 것인데 자연적으로 이치에 맞지 않는 일입니다.
④ 외부 전기장이 존재하지 않는 경우 & 전기적으로 중성이 아닌 대전된 도체
그러면, 우리의 궁금증은 외부 전기장이 없을 때 과잉전하가 존재하는 도체의 내부 모습은 어떠한가? 에 관한 것입니다. 예컨대 (-)전하가 더 많아 음으로 대전된 도체구가 있다고 해봅시다. 이 공이 중성 상태일 때는, 양전하와 음전하가 같은 전하량만큼 존재하니 자유롭게 전자들이 이리저리 움직이고 있을 겁니다. 그런데 내가 (-)전하 양념을 공에 뿌려주는 순간, 음전하가 더 많아졌지요? 이 때는 같은 종류의 전하들끼리 작용하는 '반발력'이 도체의 전하 분포를 만듭니다. 음전하들끼리 서로 반발력이 작용하여 도체 내부에 전하가 놓이지 못하고 최대한 같은 종류의 전하들끼리 멀어지는 분포 양상을 말합니다. 이게 바로 알짜 전하가 표면에만 남는다는 뜻입니다.
이게 이해가 안된다면 쉽게 아주 간단한 상황으로 예를 들어 봅시다. 어떤 도체구가 중성일 때 음전하가 -10, 양전하가 +10만큼 있다고 해봅시다. 그러다가 내가 -7의 음전하를 도체 정중앙에 뿌렸습니다. 그러면 총 전하량은 도합 -10+10-7=-7 인데, 이 -7은 이제 아무것으로부터 영향을 받지 않습니다.(외부 전기장도 없다고 가정했으므로) 그렇다면 어떻게 분포하는 것이 자연적인지를 상식적으로 생각해보면 답이 나옵니다. 답은 '서로 최대한 멀어지려고 한다'가 되겠지요? 따라서 가장 서로 거리가 먼 전하의 배열, 표면에만 알짜 전하가 남는다는 결론이 나오는 것입니다.
2) 도체 내부에서 전하밀도는 0이다.
가우스 법칙의 미분꼴을 이용하면, 도체 내부에서 전기장이 0이기 때문에
$$\nabla\cdot\mathbf{E}=0=\frac{\rho}{\epsilon_0}\;\;\Rightarrow \;\;\rho=0$$
물론 이는 진짜 전하가 하나도 없어서 0이라는 뜻은 아니고 알짜 전하밀도가 0이라는 것으로, 양전하와 음전하의 양이 같다는 것입니다.
3) 도체 내부에서 전위는 같다. 즉 도체 내부는 등전위이다.
점 $\mathbf{a}$ 와 $\mathbf{b}$ 를 도체 내부 또는 표면 상의 임의의 두 지점이라고 하면, 전위를 계산했을 때 피적분함수인 전기장이 0이므로 항상 전위도 0입니다.
$$V(\mathbf{b})-V(\mathbf{a})=-\int_{\mathbf{a}}^{\mathbf{b}}\mathbf{E}\cdot d\mathbf{l}=0 \;\;\Rightarrow \;\; V(\mathbf{b})=V(\mathbf{a})$$
4) 도체 바로 외부의 전기장은 도체 표면에 수직하다.
수직 성분이 아니라면, 도체 내부의 전기장에 의해 1)에서 했던 내용처럼 지워집니다. 표면에만 전하가 있고 내부 전기장이 0이기에, 역선은 발산하는 것으로 관찰됩니다.
또는, 전기장과 퍼텐셜의 관계를 고려했을 때 전기력선은 등전위면에 항상 수직임을 고려해도 좋습니다. 도체 내부와 표면이 등전위이기 때문에 표면을 따라 만든 선이나 면도 등전위면이라는 뜻이지요.

[참고문헌]
David Griffiths - Introduction to Electrodynamics, 4e
'전자기학(Electromagnetics) > 정전기학' 카테고리의 다른 글
| 전자기학에서의 유일성 정리 (Uniqueness Theorem in Electromagenetics) (1) | 2021.01.19 |
|---|---|
| 전위와 라플라스 방정식 (Electric potential and Laplace Equation) (0) | 2021.01.19 |
| 점전하 분포의 에너지 (The Energy of a point charge distribution) (0) | 2021.01.12 |
| 전기장, 전위의 경계조건 (Boundary condition of $\mathbf{E}, V$) (0) | 2021.01.12 |
| 전위, 전기 퍼텐셜 (Electric Potential) (0) | 2021.01.08 |


댓글