벡터의 크기와 길이에 대한 정보를 다루기 위해서는 흔히 절댓값 벡터로 알고 있는 노름(norm)에 대한 지식이 필요합니다. 노름은 번역을 하기가 힘들어 번역서에서도 그냥 노름이라 말하지만, 읽을 때는 '놈'에 가깝습니다. 그러나 놈은 한국어로 좋은 뜻은 아닐 뿐더러 R 발음을 살려주기 위해서 노름이라고 적어둔 책이 좀 더 많습니다. 저는 아무 표현이나 다 사용할 것입니다.
노름은 고등학교 수학에서 사용했던 절댓값의 일반화되고 추상화된 개념입니다. 길이나 거리를 측정하기 위한 수단으로서 사용되는 경우가 대부분입니다. 지금은 선형대수학 포스팅을 하고 있기 때문에 선형대수학의 노름을 위주로 설명하겠지만, 공간이라는 키워드에 초점을 맞춘다면 노름을 특정 정의를 만족하는 노름 공간의 원소로서 관찰하는 것도 가능합니다. 이에 대한 개념이 필요하시다면 해당 링크를 눌러 찾아보시면 되겠습니다.
1. 선형대수학에서 노름
1) 정의
선형대수학에선 다음과 같이 내적에 근호를 씌움으로서 노름을 정의하게 됩니다.
정의($L.A$) 6-2) 놈의 정의
내적공간 $V$와 벡터 $x\in V$에 대하여 $x$의 '노름(norm)' 또는 길이(length)를
$$\left\| x \right\|=\sqrt{\left\langle x,x \right\rangle}$$ 로 정의한다.
정의($L.A$) 6-3) 유클리드 놈(Euclidean norm)
$V=F^n$ 과 $x=\left( a_1,\cdots ,a_n \right)$ 에 대하여
$$\left\| x \right\|=\left\| a_1,\cdots ,a_n \right\|=\sqrt{\sum_{i=1}^{n}\left| a_i \right|^2}$$ 를 $x$에 대한 '유클리드 길이(Euclid length)'라 한다.
유클리드 길이는 기하와 벡터에서부터 배웠던 벡터의 절댓값을 연산하여 얻은, 3차원상에서 두 점 사이의 최단 직선 거리를 구하는 방법으로도 알려져 있는 바로 그 개념입니다. 그리고 이것은 선형대수학에서 자기 자신끼리의 내적에 근호를 취해주는 방식으로 연산을 하여 구할 수 있습니다. 노름 공간에도 적어두었지만, 비유클리드 기하학으로 가면 노름을 노름 공간의 원소 정의를 만족하지만 유클리드 길이와는 다른 방식으로 길이를 정의할 수도 있게 됩니다. 유클리드 놈이 아닌 다른 종류의 놈은 기하학, 해석학, 함수해석학 등에서 구체적으로 다룹니다. 다만 지금은 선형대수학을 다루고 있고,그쪽으로 너무 가면 삼천포이니 지금은 선형대수학의 범위에서만 놀아 볼 것입니다.
2) 노름의 성질
정리($L.A$) 6.2
$F$-내적공간 $V$와 임의의 벡터 $x,y\in V$, 스칼라 $c\in F$ 에 대하여 다음이 성립한다.1
① $\left\| cx \right\|=\left| c \right|\left\| x \right\|$
② $\left\| x \right\|=0\;\;\Rightarrow \;\;\ x=\mathbf{0}$
증명) ① $$\begin{align*}
\left\| cx \right\|&=\sqrt{\left\langle cx,cx \right\rangle}=\sqrt{c\left\langle x,cx \right\rangle}
\\\\&=
\sqrt{c\overline{\left\langle cx,x \right\rangle}}=\sqrt{c\overline{c}\left\langle x,x \right\rangle}\\\\&=
\left| c \right|\sqrt{\left\langle x,x \right\rangle}=\left| c \right|\left\| x \right\|
\end{align*}$$
② $\left\langle x,x \right\rangle=0 \;\;\Rightarrow \;\; x=\mathbf{0} $ 이므로, $\left\| x \right\|=0\;\;\Rightarrow \;\; x=\mathbf{0}$ 이다.
이외에도 노름은 코시-슈바르츠 부등식과 삼각부등식을 만족합니다. 해당 내용이 길기 때문에 다음 포스팅에 따로 적어둘 예정입니다.
2. 노름 공간
선형대수학의 범위를 넘어, 일반적으로 놈의 정의는 다음과 같이 합니다.
정의($L.A$) 6-4) 놈의 정의
벡터공간 $V$에 대하여 $V$ 상에서의 노름(Norm)은 다음 조건을 만족하는 함수 $f$
$$f=\left\| \cdot \right\| : V\rightarrow \mathbb{R}$$ 으로 정의된다.
① 모든 $x\in V$ 에 대하여 $\left\| x \right\|
\geq 0$ 이고 $\left\| x \right\|=0\;\;\Leftrightarrow \;\;x=\mathbf{0}$ 이다.
② $c\in \mathbb{C}$ 에 대하여 $\left\| cx \right\|=\left| c \right|\left\| x \right\|$
③ 임의의 $x,y\in V$ 에 대하여 $\left\| x+y \right\|\leq \left\| x \right\|+\left\| y \right\|$ 이 조건은 '삼각부등식(Triangle inequality)'라고도 부른다.
위의 세 조건을 만족하는 벡터공간을 '놈(벡터)공간(Normed vector spaces)' 라 부른다.
그러니 함수 $f$는 벡터에서 실수로 가는 함수이며 선형성을 가지므로 선형범함수의 일종입니다. 이러한 조건을 만족하는 벡터공간을 특별히 놈공간이라 불러주겠다는 것입니다.
놈은 왜 정의하고 왜 필요한걸까요? 놈은 '크기'라는 성질을 수학적으로 일반화하여 정의한 것입니다. 물리적으로 우리가 어떤 대상의 크기를 측정할 때 - 행성의 크기라던지, 과일의 길이라던지, 토지의 면적이라던지 - '크기'라는 성질은 0이 나왔다면 측정한 대상 자체가 0이었어야 하고(=1번 조건), 스칼라 배를 해서 크기를 재나 크기를 재서 스칼라 배를 하나 같아야 하며(=2번 조건), 둘의 크기를 각각 더했을 때가 둘을 더한 다음 크기를 쟀을 때보다 같거나 커야 한다(=3번 조건)는 조건들을 만족해야 한다는 것이죠.
대수학은 수학에서 여러 문자 등을 통해 현상이나 진리들을 '대신(代)' 표현하겠다는 것입니다. 즉 '크기'라는 성질을 노름함수 $f$로 대신 표현하겠다는 것이죠. 수학은 일반화를, 추상화를 향해 나아가므로 노름공간은 그냥 벡터공간의 한 일종 뿐이며 위의 정의를 달달 외울 것이 아니라, 전 문단에서 설명드린 것처럼 '크기'라는 성질과 연관지어 생각하면 좋습니다.
벡터공간의 범위를 내적공간으로 줄이게 되면, 벡터의 놈을 $\left\| x \right\|=\sqrt{\left\langle x,x \right\rangle}$ 라고 정의했을 때 놈 공간의 조건들을 모두 만족시키게 되므로, 선형대수학에서 내적공간의 원소인 벡터 $x$에 대해서 놈을 이와 같이 정의한 것입니다. 그러므로 벡터의 '크기'에 관한 연산을 하거나 성질을 다룰 때는 놈을 사용하는 것이며, 원칙적으로 놈의 기호는 짝대기가 두개입니다. 흔히 우리가 숫자의 크기는 절댓값 기호를 통해 나타내고 이는 짝대기가 하나지만, 벡터공간을 배운 이상 벡터의 크기는 엄밀히 말하면 놈이니 짝대기 두개 기호를 써야 하는 것이고, 스칼라에 대해서는 짝대기 하나를 쓰는 것이 원칙인 것입니다.
놈은 의미상 거리공간과 공통점이 있으면서도 정의가 다르다는 점때문에 혼란을 야기하는 경우가 있습니다. 결론적으로 보면 모든 놈 공간은 거리공간이지만 모든 거리공간이 놈 공간은 아닙니다. 다시 말하면 모든 놈 공간에서는 거리를 정의할 수 있으나, 거리가 정의된다고 해서 반드시 놈을 정의할 수 있다고 볼 수는 없습니다. 또한 놈 공간의 정의를 보면 기본적으로 놈은 벡터공간이어야 합니다. 하지만 거리공간의 공리에서 주어진 공간(집합)이 벡터공간의 공리를 만족해야 한다는 내용은 어디에도 없음을 알 수 있습니다.
2. 여러가지 놈
놈은 사실 놈 공간의 조건만 만족시키면 무엇이든 만들 수 있는 것이라서 하나만 존재하는 것은 아닙니다. 놈은 실제 여러 가지 종류가 있습니다. 선형대수학에서는 주로 유클리드 놈 정도만 학습하고 응용하지만, 해석학이나 위상수학에 가면 여러 가지 놈을 다루게 됩니다.
정의($L.A$) 6-5) 여러가지 놈
$\mathbf{x}\in \mathbb{R^n}$ 이라 하자.
① $\mathbf{x}$ 의 '유클리드 놈(Euclidean norm)' 또는 크기(magnitude)는 스칼라
$$\left\| \mathbf{x} \right\|:=\sqrt{\sum_{k=1}^{n}\left| x_k \right|^2}=\sqrt[]{\left\| \mathbf{x}_2 \right\|}$$ 로 정의한다. 이는 '$l2$ 놈'이라고 부르기도 한다.
② '택시 거리(Taxicab norm)' 또는 '맨해튼 놈(Manhattan norm)', 또는 '$l1$ 놈'은 놈의 일종으로 다음과 같이 정의한다. $x\in V$ 이고 $x$의 $i$번째 성분이 $a_i$ 일 때,
$$\begin{align*}
\left\| x \right\|&=\left\| a_1 \right\|+\left\| a_2 \right\|+\cdots +\left\| a_n \right\|=\sum_{i=1}^{n}\left\| a_n \right\| \\\\&
\Leftrightarrow \left\| \mathbf{x} \right\|_1:=\sum_{k=1}^{n}\left| x_k \right|
\end{align*}$$
③ '상한 놈(Sup-norm)'은 스칼라
$$\left\| \mathbf{x} \right\|_{\infty}:=\max \left\{ \left| x_1 \right|,\cdots ,\left| x_n \right| \right\}$$ 으로 정의한다.
④ 두 점 $\mathbf{a},\mathbf{b}\in \mathbb{R}^n$ 의 '유클리드 거리(Euclidean distance)'는 스칼라
$$d(\mathbf{a},\mathbf{b}):=\left\| \mathbf{a}-\mathbf{b} \right\|$$ 이다.
여기서 특이한 노름을 하나 살펴보겠습니다. 우리가 보통 다루는 기하학인 유클리드 기하학에는 5가지 공리와 공준이 존재합니다. 그 중 5번째 공준을 비틀어 만든 비유클리드 기하학 중 택시 기하학에서도 놈을 정의할 수 있는데, 유클리드 놈과 그 형태가 다릅니다.
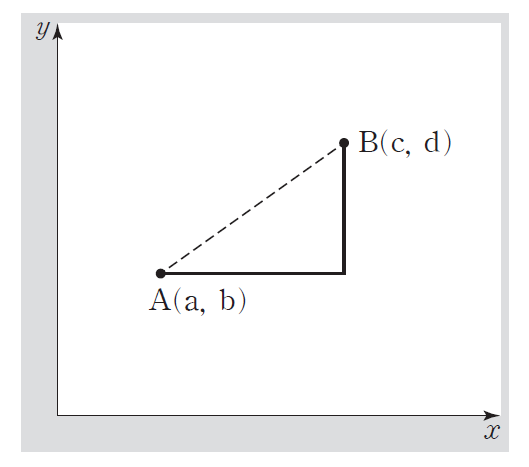
우선 정의한 대로 해석을 해보자면 예컨대 위의 평면의 두 점 $A,B$ 사이의 맨해튼 놈은 최단거리로 가는 경로의 길이가 아니라 뒤집어진 ㄴ자로 갈 때 이 경로의 길이가 됩니다. $x$성분의 절댓값 + $y$성분의 절댓값이 되니 때문이죠.
이름이 왜 택시, 맨해튼일까요? 맨해튼은 뉴욕의 심장부로 우리가 뉴욕을 떠올렸을 때 유명한 것들이 다 모여있는 섬입니다. (공교롭게도 이 글을 작성하기 1주일 전까지 뉴욕 여행을 다녀왔었습니다..) 맨해튼을 포함해 미국의 대도시들은 길거리가 완전히 좌표평면의 정사각형처럼 배치되어 있어, 한 블럭 두 블럭 이렇게 블럭이라는 말로 표현을 하죠. 전망대에 올라가서 보면 정말 사각형들이 조밀하게 모여 있고 칼로 빵을 자른듯이 엄밀하게 블럭들이 나뉘어 있습니다.

이러한 도시에 사는 택시기사는 출발지에서 도착지로 갈 때 최단거리, 곧 대각선처럼 이동하지 못하고 반드시 가로로 몇 블럭, 세로로 몇 블럭 이렇게 이동해야 합니다. 그래서 택시기사에게 두 점 $A,B$ 사이의 거리는 $(d-b)+(c-a)$ 가 되는 것이죠. 그래서 택시 거리, 맨해튼 노름이라는 말이 붙은 것입니다.
비유클리드 기하학은 유클리드 기하학에서와 놈의 정의가 다르니 당연히 여러 성질들이 달라집니다. 똑같이 원의 방정식을 세웠을 때 유클리드 기하학에서는 우리가 아는 둥근 모양의 원 곡선이 나오지만, 택시 기하학에서는 마름모가 원의 방정식을 갖습니다. 이렇게 벡터공간의 정의는 정말 추상화된 대상이며 그 아래로 범위를 점점 좁혀갈수록 예전엔 다 같은 것인줄 알았던 것들이 세분화되어 다른 것이라는 사실을 알아가게 되는 것이 대수학의 묘미라고 할 수 있겠네요.
[참고문헌]
Linear Algebra : S.Friedberg, A.Insel, L.Spence, 5e, PEARSON
- 당연한 말이지만 원래 벡터는 볼드체로 표기하는 것이 맞으나, $V$의 원소임이 적혀 있다면 볼드체로 적혀 있지 않더라도 벡터로 생각해주시기 바랍니다. [본문으로]
'선형대수학(Linear Algebra) > 내적공간' 카테고리의 다른 글
| 그람-슈미트 직교화 과정(Gram-Schmidt orthogonalization process) (0) | 2022.12.18 |
|---|---|
| 벡터의 직교와 정규화(Orthogonality and normalization) (0) | 2022.07.17 |
| 삼각 부등식의 증명(Triangle inequality) (0) | 2022.07.12 |
| 코시-슈바르츠 부등식 증명(Cauchy-Schwarz inequality) (0) | 2022.07.12 |
| 내적공간 (Inner product space) (0) | 2022.02.13 |

댓글