행렬식은 영어로 'Determinants'라 하여 직역하면 행렬의 식이라기보단 무언가를 판별이나 결정하는 식이라는 뜻에 가깝습니다.실제로도 원래 연립방정식의 해가 존재하려면 어떤 조건이 필요한지를 연구하는 과정에서 태동한 것입니다. 그러니 행렬보다 행렬식을 먼저 다루기 시작했다는 말도 일리가 있습니다.
행렬식을 정의하고 구하는 방법은 유일하지 않은데, 이는 어렵게 들어가면 행렬식은 사실 다중 선형성(n-linearity), 교대(alternating), 그리고 항등행렬의 행렬식의 값이 1이라는 세 가지 성질을 만족하는 유일한 선형 범함수(Linear functional)에 해당하고 이를 만족하는 하나의 정의가 있지만, 유일성이 보장되어 몇가지 다른 표현을 할 수 있기 때문입니다. 이 성질을 모두 가장 정확히 만족하는 정의는 치환(permutation)을 이용하는 것이고, 그러나 이는 대수학의 개념을 알아야 하므로 가장 널리 쓰이는 방법은 '여인수 전개(Cofactor, Laplace development)'이며 연립방정식을 풀 땐 '크래머의 규칙(Cramer's Rule)', 그냥 단순 계산이면 $3\times 3$ 행렬에 한해 '사루스 법칙(Sarrus rule)' 을 사용합니다. 하나 하나씩 살펴봅시다.
1. 정의
1) 치환으로 정의
본인은 여인수 전개(아래에서 설명)를 기대하고 들어왔는데, 아래의 황당한 수식을 보고 벙찐 분들은 굳이 이 정의를 필수적으로 알 필요까진 없습니다. 아마 수학과가 아니라면 행렬식을 이렇게 배우지 않을 가능성이 높으며, 여러분들이 알고 있는 여인수 전개로 행렬식을 계산하면 됩니다. 증명과 수학적 엄밀성에 매달리는 수학과가 아니라면 꼭 알아야 하는 건 아닙니다. 다만 이 치환의 방법은 행렬식의 몇가지 규칙들을 정의하는데 유용히 쓰이기는 합니다. 여기서 쓰이는 수학적 도구들은 치환, 순환, 호환, 부호함수 입니다.
정사각행렬 $A\in M_n(F)$의 행렬식(determinant)은 $\mathrm{det}A$ 또는 $\left | A \right |$ 로 나타내고 다음과 같이 정의한다.
$$\mathrm{det}A=\sum_{\sigma \in S_n}\prod_{i=1}^{n}a_{i\sigma(i)}
=\sum_{\sigma \in S_n}\mathrm{sgn}(\sigma)\,a_{1\sigma(1)}a_{2\sigma(2)}\,\cdots\,
a_{n\sigma(n)}$$
행렬식은 $S_n$의 치환을 성분의 일부로 삼고 부호함수의 곱으로 정의를 합니다. 그러나 딱딱한 위의 식만 봐서는 당연히 무슨 뜻인지 알 수 없겠죠? 예제를 봅시다.
예제 1) $2\times 2$ 행렬 $A=\begin{pmatrix}
a_{11} &a_{12} \\
a_{21} & a_{22}
\end{pmatrix}$ 의 행렬식을 구하라.
정사각행렬의 사이즈가 $n$입니다. 그러면 $S_2$이므로 두개의 치환
$$\sigma_1=\begin{pmatrix}
1 &2 \\
1 & 2
\end{pmatrix}=\begin{pmatrix}
1 & 2
\end{pmatrix}\begin{pmatrix}
1 & 2
\end{pmatrix}\;\;,\;\;\sigma_2=\begin{pmatrix}
2 &1 \\
1 &2
\end{pmatrix}=\begin{pmatrix}
1 & 2
\end{pmatrix}$$
은 순서대로 각각 짝치환, 홀치환이므로 부호는 $+1,-1$ 입니다. 첫 치환 $\sigma_1$은 항등치환으로 $\sigma(1)=1,\sigma(2)=2$ 라서
$$\mathrm{sgn}(\sigma_1)a_{1\sigma(1)}a_{2\sigma(2)}=+a_{11}a_{22}$$
같은 방법으로 $\sigma_2$에 대한 치환과 부호함수를 고려하면
$$\mathrm{sgn}(\sigma_2)a_{1\sigma(1)}a_{2\sigma(2)}=-a_{21}a_{12}$$
이기 때문에, $2\times 2$ 행렬의 행렬식은
$$\mathrm{det}A=a_{11}a_{22}-a_{12}a_{21}$$
$3\times 3$ 정사각행렬의 행렬식은 다음과 같다.
$$\mathrm{det}A=\left ( a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{31}a_{21}a_{31} \right )
-\left ( a_{13}a_{22}a_{31}+a_{11}a_{23}a_{32}+a_{12}a_{21}a_{33} \right )$$
이것을 보이려면 $S_3$의 모든 치환을 구하고, 짝치환과 홀치환에 대해 부호를 붙여주면 됩니다. 6개의 치환을 밑에 적어두었는데, 이전에 호환에서 이미 살펴보았던 내용으로 위의 3개는 짝치환, 아래 3개는 홀치환입니다.
$$\begin{pmatrix}
1 & 2 &3 \\
1 &2 &3
\end{pmatrix}=\begin{pmatrix}
1 & 2
\end{pmatrix}\begin{pmatrix}
1& 2
\end{pmatrix}$$
$$\begin{pmatrix}
1 & 2 &3 \\
3 &1 &2
\end{pmatrix}=\begin{pmatrix}
1 & 3 & 2
\end{pmatrix}=\begin{pmatrix}
1 & 2
\end{pmatrix}\begin{pmatrix}
1& 3
\end{pmatrix}$$
$$\begin{pmatrix}
1 & 2 &3 \\
2 &3 &1
\end{pmatrix}=\begin{pmatrix}
1 & 2 & 3
\end{pmatrix}=\begin{pmatrix}
1 & 3
\end{pmatrix}\begin{pmatrix}
1 & 2
\end{pmatrix}$$
$$\begin{pmatrix}
1 & 2 &3 \\
1 &3 &2
\end{pmatrix}=\begin{pmatrix}
2 & 3
\end{pmatrix}\;\;,\;\;
\begin{pmatrix}
1 & 2 &3 \\
3 &2 &1
\end{pmatrix}=\begin{pmatrix}
1 & 3
\end{pmatrix}\;\;,\;\;
\begin{pmatrix}
1 & 2 &3 \\
2 &1 &3
\end{pmatrix}=\begin{pmatrix}
1 & 2
\end{pmatrix}$$
2) 여인수 전개(라플라스 전개)
공업수학이나 수리물리학에서 행렬식을 구하는 방법은 거의 대부분 여인수 전개입니다.
행렬 $A\in M_n(F)$의 행렬식은 다음과 임의의 $i$행에 대한 여인수 전개로 정의할 수 있다.
$$\mathrm{det}A=\sum_{j=1}^{n}\left ( -1 \right )^{i+j}a_{ij}\,\mathrm{det}\left ( \tilde{A_{ij}} \right )$$
이 때 $C_{ij}=\left ( -1 \right )^{i+j}\mathrm{det}(\tilde{A_{ij}})$ 는 '여인수(Cofactor)'라 하며 $\tilde{A_{ij}}$ 는 $A$의 $i$행과 $j$열을 제외한 나머지 성분으로 만든 $(n-1)\times(n-1)$ 행렬식으로 '소행렬식(Minor)'이라고 한다. 소행렬식은 $M_{ij}$ 라 표기하기도 한다.
이 방법은 미적분학에서 벡터의 외적(Outer product)를 셈할 때 사용하는 행렬식 방법과 똑같습니다. $3\times 3$ 행렬식을 구할 땐 3차원 외적을 할 때는 1행이 기저벡터였지만 행렬식에선 그냥 숫자로 구성되어 있다는 점만 다릅니다. 이 정의는 특별한 새로운 개념을 알아야 하는 것이 아니기에 가장 널리 사랑받는 방법입니다.
예제 2) 행렬 $A=\begin{pmatrix}
1 & 2 &-1 \\
3 & 0 & 4\\
-1 & 7 & 2
\end{pmatrix}$ 의 행렬식을 2행에 대한 여인수 전개로 구하라.
$$\mathrm{det}A=\left ( -1 \right )^{2+1}\cdot 3\begin{vmatrix}
2 &-1 \\
7 &2
\end{vmatrix}+\left ( -1 \right )^{2+2}\cdot 0\begin{vmatrix}
1 &-1 \\
-1 &2
\end{vmatrix}+\left ( -1 \right )^{2+3}\cdot 4 \begin{vmatrix}
1 &2 \\
-1 &7
\end{vmatrix}=-69$$
이 예제로부터 중요한 사실을 알 수 있습니다. 여인수 전개를 할 때는 특정 행(이 문제에서는 2행)을 선택하고 그것에 대한 전개를 하는데, 그 행 성분이 각각 곱해집니다. 그런데 0이 있다면 계산량이 확 줄어드는거 보이시나요? 그리하여 행렬식을 계산할 때 성분으로 0이 존재한다면 여인수 전개에 의한 방법이 유리하며, 그 0이 포함된 행을 선택하는 것이 좋습니다. 만약 한 행이나 열 전체가 0이라면 어떻게 될까요? 그 행이나 열에 대해 여인수 전개하면 알겠지만 행렬식의 값은 반드시 0이 나옵니다.
3) 사루스 공식
$3\times 3$ 행렬에 한해서 다음의 규칙을 이용하면 행렬식을 빠르게 구할 수 있습니다. 이건 수식 작성으로 만들지 못하기 때문에 그냥 퍼왔습니다.
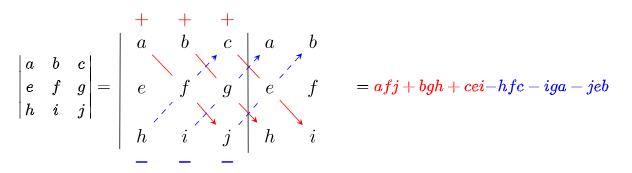
사용 방법은 다음과 같습니다. $3\times 3$ 행렬식 우측 짝대기 바깥에 행렬의 1,2열을 추가로 그려 넣습니다. 그 다음 우하향 대각선(그림의 빨간색 대각선)으로 3개의 숫자를 3번 곱해 양수를 달아주고, 우상향(파란색) 대각선으로도 숫자를 3번 3개씩 곱해 음수를 달아줍니다. 이렇게 6개의 숫자를 모두 더하면 바로 행렬식을 구할 수 있습니다. 이 방법은 $3\times 3$ 행렬식에 대해서는 가장 빠른 방법입니다.
'선형대수학(Linear Algebra) > 행렬과 행렬식' 카테고리의 다른 글
| 크래머 공식(Cramer's Rule) (0) | 2020.12.11 |
|---|---|
| 행렬식의 다중 선형성(n-linearity, multi linearity of determinants) (0) | 2020.12.10 |
| 가우스-조르당 소거법(Gauss-Jordan Elimination) (1) | 2020.12.02 |
| 가역행렬과 가역성에 대한 모든 정리 (Invertibility of the matrix) (0) | 2020.12.01 |
| 행 사다리꼴, 기약 행 사다리꼴 행렬 (Reduced Row-Echelon form) (2) | 2020.12.01 |
댓글