이미 위상공간인 두 집합이 제시되었을 때, 이들을 데카르트 곱으로 묶어 집합을 만들고 그 위에서 위상을 만들 수 있습니다. 이에 대해 알아봅시다.
1. 곱 위상
1) 정의
정의($T.P$) 2-13) 곱 위상
$(X,\mathcal{T}),(Y,\mathcal{T}')$ 을 위상공간이라고 하자. 데카르트곱 $X\times Y$ 에서의 '곱 위상(product topology)이란', 모든 각각의 열린집합 $U\subseteq X\;,\;V\subseteq Y$ 들로 이루어진 데카르트곱 $U\times V$ 를 기저원소 $B\in\mathcal{B}$ 로 가지는 기저 $\mathcal{B}=\displaystyle \bigcup_{U\subseteq X,V\subseteq Y}^{}(U\times V)$ 에 의해 생성되는 위상을 말한다.
으레 그래왔듯이, 실제로 위와 같이 정의하면 $\mathcal{B}$ 가 기저가 된다는 것을 보여야만 합니다. 예제로 돌려서 확인해 보도록 하겠습니다.
예제 1) 위와 같이 곱 위상을 정의했을 때 실제로 $\mathcal{B}=\displaystyle \bigcup_{U\subseteq X,V\subseteq Y}^{}(U\times V)$ 가 기저의 정의를 만족하는지 확인하여라.

Sol) 기저의 정의를 만족하는지 확인하자.
i) 덮개 조건을 만족할까? : 임의의 $(x,y)\in (X\times Y)$ 를 생각했을 때, $U\subseteq X$ 이고 $V\subseteq Y$ 일 때 $(x,y)\in (U\times V)$ 인 $U,V$ 가 존재해야 한다고 볼 수 있다. 그런데 그냥 $U=X, V=Y$ 로 택해버리면 자명하게 덮개 조건이 성립한다. 즉 임의의 $(x,y)$ 는 그냥 $X\times Y$ 에 들어있는데, 위상공간 $X,Y$ 자체의 데카르트곱이 기저원소로 작동할 수 있는 상황인 것이다.
ii) 교집합 조건 : $X\times Y$ 의 두 기저원소 $U_1\times V_1$ 과 $U_2\times V_2$ 를 생각하자. 그러면
$$(U_1\times V_1)\cap (U_2\times V_2)=(U_1\cap U_2)\times (V_1\cap V_2)$$
가 성립하고, $U_1,U_2\subseteq X$ 는 $X$ 에서 열린집합이며 $X$ 는 위상공간이기 때문에, $U_1\cap U_2$ 또한 $X$ 에서 열린집합이 된다.1 같은 이유로 $V_1\cap V_2$ 또한 $Y$ 위에서의 열린집합이다. 그러면 $U_1\cap U_2\in\mathcal{T}$ 와 $V_1\cap V_2\in\mathcal{T}'$ 이 성립하므로,
$$(x,y)=U_3\times V_3:=(U_1\cap U_2)\times (V_1\cap V_2)\subseteq(U_1\times V_1)\cap (U_2\times V_2)$$
가 되어 교집합 조건도 만족된다. 따라서 $\mathcal{B}$ 는 주어진 위상공간 $X\times Y$ 에서의 위상의 기저 정의를 만족한다. $_\blacksquare$
예제 2) 기저집합 $\mathcal{B}$ 는 위상공간 $X\times Y$ 상에서 위상이 되지 못함을 보여라.
Sol) 위 정의의 두번째 합집합 조건을 생각해보자. $(U_1\times V_1)\cup (U_2\times V_2)=(U_1\cup U_2)\times (V_1\cup V_2)$ 에서 $(U_1\cup U_2)\times (V_1\cup V_2)$ 이 기저집합 $\mathcal{B}$ 에 항상 포함된다고 볼 수 없다. 즉 기저의 정의를 생각해보았을 때 $U_1\cup U_2= U_3$ 이고 $V_1\cup V_2= V_3$ 인 $U_3, V_3$ 가 항상 $\mathcal{B}$ 에 존재한다고 보장할 수가 없다. $_\blacksquare$
예제 3) 두 위상공간이 $X=\{ 1,2 \}, Y=\{ a,b,c \}$ 으로 주어져 있고, $\mathcal{T}=\{ \emptyset, X, \{ 1\} \}, \mathcal{T}'=\{ \emptyset, Y, \{ a\}, \{ b,c\} \}$ 이라고 하자. 여기서 $\mathcal{T},\mathcal{T}'$ 은 각각 $X,Y$ 위에서의 위상이다. 이때 $\mathcal{B}=\{ U\times V\mid U\in\mathcal{T},V\in \mathcal{T}'\}$ 이라고 할 때 기저집합 $\mathcal{B}$ 의 원소를 원소나열법으로 모두 찾아보아라.
Sol) 결국 각각의 열린집합들 $U\in\mathcal{T}$ 와 $V\in\mathcal{T}'$ 을 하나씩 뽑아서 데카르트곱을 만드는 것에 불과하다. $\mathcal{T}$ 와 $\mathcal{T}'$ 의 원소의 개수가 각각 $3,4$ 이므로, 일단 순서쌍의 개수는 $3\times 4=12$ 개가 발생한다. 이를 모두 적어보면 다음과 같다.
$$\begin{align*}
1. &\ \emptyset \times \emptyset = \emptyset \\
2. &\ \emptyset \times Y = \emptyset \\
3. &\ \emptyset \times \{a\} = \emptyset \\
4. &\ \emptyset \times \{b, c\} = \emptyset \\
5. &\ X \times \emptyset = \emptyset \\
6. &\ X \times Y = \{(1, a), (1, b), (1, c), (2, a), (2, b), (2, c)\} \\
7. &\ X \times \{a\} = \{(1, a), (2, a)\} \\
8. &\ X \times \{b, c\} = \{(1, b), (1, c), (2, b), (2, c)\} \\
9. &\ \{1\} \times \emptyset = \emptyset \\
10. &\ \{1\} \times Y = \{(1, a), (1, b), (1, c)\} \\
11. &\ \{1\} \times \{a\} = \{(1, a)\} \\
12. &\ \{1\} \times \{b, c\} = \{(1, b), (1, c)\} \\
\end{align*}$$
물론, 공집합을 반복해서 적지 않는 것이 관례이기 때문에, 이들을 모아 기저집합을 원소나열법으로 모두 적으면 다음과 같다.
$$\begin{align*}
\mathcal{B} &= \{U\times V\mid U\in\mathcal{T},V\in\mathcal{T}' \}
\\\\&=
\left\{ \right.\emptyset, X\times Y=\left\{ (1, a), (1, b), (1, c), (2, a), (2, b), (2, c) \right\},
\\\\& \left\{ (1, a), (2, a) \right\}, \left\{ (1, b), (1, c), (2, b), (2, c) \right\},
\\\\& \left\{ (1, a), (1, b), (1, c) \right\},\left\{ (1, b), (1, c) \right\} , \{ (1,a) \}
\left. \right\}
\end{align*}$$
그리고 여기서 $\mathcal{B}\subseteq \mathcal{P}(X\times Y)$ 임을 알 수 있다. 또한, 추가로 이 기저에 의해 만들어지는 위상을 생각해보면
$$\mathcal{T}_{\mathcal{B}} = \{ W=\displaystyle \bigcup_{\alpha\in I}^{}B_{\alpha}\subseteq (X\times Y)\mid \forall \alpha\in I\;,\; B_{\alpha}=U\times V\in \mathcal{B}\;\; \text{where}\;U\in \mathcal{T}\;,\;V\in \mathcal{T}'
\}$$
와 같이 적을 수 있을 것이다. $_\blacksquare$
2) 성질
정리($T.P$) 2.11)
$\mathcal{B},\mathcal{C}$ 를 각각 위상공간 $X,Y$ 의 기저라고 하자. 그러면 다음의 집합족
$$ \mathcal{D}=\{ B\times C\mid B\in\mathcal{B}\;,\;C\in\mathcal{C}\}$$ 는 위상공간 $X\times Y$ 위에서의 위상의 기저가 된다. 즉, 이 위상은 $\mathcal{T}_{\mathcal{D}}$ 라 적을 수 있을 것이다.
증명) 열린집합 $W\subseteq (X\times Y)$ 를 생각하고, 각각의 $(x,y)\in W$ 에 대하여, $(x\times y)\in (U\times V)\subseteq W$ 가 성립하는 기저원소 $U\times V$ 가 존재함을 보이면 정리($T.P$) 2.3) 에 의하여 증명할 수 있다.
가정에 따라 $\mathcal{B},\mathcal{C}$ 가 각각 위상공간 $X,Y$ 의 기저이므로, 임의의 $(x,y)$ 에 대하여 $x\in B\subseteq U$ 이고 $y\in C\subseteq V$ 인 기저원소 $B,C$ 를 항상 선택할 수 있다. 그러면 $(x,y)\in (B\times C)\subseteq (U\times V)\subseteq W$ 가 성립한다. 따라서 $\mathcal{D}$ 는 정리($T.P$) 2.3) 에 의하여 위상공간 $X\times Y$ 의 기저가 된다.$_\blacksquare$
예제 4) 보통위상이란 $\mathcal{B}_u=\{ (a,b)\mid a,b\in\mathbb{R}\;,\; a<b\}$ 와 같이 기저원소가 모든 실직선 $\mathbb{R}$ 에서의 열린구간으로 구성된 집합족을 기저로 하여 생성되는 위상 $\mathcal{T}_{\mathcal{B}_u}$ 로 정의된다. 이때 집합 $X=\mathbb{R}$ 이 위상공간이 되는 것이다. 이 보통위상은, $\mathbb{R}^2$ 에서의 곱 위상에 해당함을 보여라.
Sol) 보통위상의 기저는 $\mathcal{B}_u=\{ (a,b)\mid a,b\in\mathbb{R}\;,\; a< b \}$ 에 해당한다. 이것에 대응되는 위상공간이 $\mathbb{R}$ 이므로, 정리($T.P$) 2.11) 에 따라 기저 $\mathcal{D}$ 를
$$\begin{align*}
\mathcal{D} &= \left\{ B\times C\subseteq \mathbb{R}^2\mid B\in\mathcal{B}_u\;,\;C\in\mathcal{B}_u \right\}
\\\\&=\left\{ (a,b)\times (c,d)\mid a,b,c,d\in\mathbb{R}\;,a< b\;\wedge \;c < d \right\}
\end{align*}$$
와 같이 설정해줄 수 있고, 따라서 이 정리에 의해 $\mathcal{D}$ 는 위상공간 $\mathbb{R}^2=\mathbb{R}\times \mathbb{R}$ 위에서의 위상의 기저가 된다. 그런데 이 표현은 보통위상의 기저식을 단순히 2차원 식으로 늘린 것에 불과하다. 즉, 실수 평면 $\mathbb{R}^2$ 에서의 보통위상을 생성하는 기저인 것이다. 그러므로, $\mathcal{D}$ 는 위상공간 $\mathbb{R}^2$ 위에서의 곱 공간의 기저이면 보통위상의 기저이기도 하다는 뜻이다.2 $_\blacksquare$
2. 사영
곱 위상과 같이 소개할 수 있는 사영의 개념이 있습니다. 사영은 뒤에 가서 상자 위상을 소개할 때 다시 등장하니, 개념을 간단히 알아둘 필요가 있습니다.
1) 정의
정의($T.P$) 2-14) 사영
두 함수 $\pi_1 : X\times Y\longrightarrow X$ 와 $\pi_2 : X\times Y\longrightarrow Y$ 를 $\pi_1(x,y)=x$, $\pi_2(x,y)=y$ 로 정의하자. 그러면 $\pi_1,\pi_2$ 는 위상공간 $X\times Y$ 에서의 각각 첫번째, 두번째 변수에 대한 '사영(projection)'이라고 한다.
사영은 고등학교 수학의 기하나 선형대수학에서의 정사영 느낌으로 볼 수 있습니다. 단순히 $x$ 또는 $y$ 좌표만을 끄집어 내는 역할을 하는 함수에 해당합니다.
또한 사영은 이와 같이 정의하면 그 자체로 전사함수(surjective function)이 됩니다. 그 이유는, 예컨대 $\pi_2$ 를 예시로 들자면, 임의의 $y\in Y$ 에 대해 $y=\pi_2(x,y)$ 가 되게 하는 $(x,y)$ 를 뽑아낼 수 있기 때문입니다. 단순히, $\pi_2$ 에 들어갈 모든 $(x,y)$ 에 대해 이것의 $y$ 값은 반드시 공역 $Y$ 에 포함되어야 하기 때문에, 치역과 공역이 같아지는 것으로 볼 수 있습니다.
정리($T.P$) 2.12)
$X$ 가 위상공간일 때 $U\subseteq X$ 를 $X$ 위에서의 열린집합이라고 하자. 그러면 $\pi_1^{-1}(U)=\left\{ (x,y)\in X\times Y \mid \pi_1(x,y)=x\in U \right\}=U\times Y $ 가 성립하고, 이때 $U\times Y\subseteq X\times Y$ 는 $X\times Y$ 에서의 열린집합이 된다.
비슷하게, 위상공간 $Y$ 에 대해 $V\subseteq Y$ 를 $Y$ 위에서의 열린집합이라고 하면 $\pi_2^{-1}(V)=\left\{ (x,y)\in X\times Y \mid \pi_2(x,y)=y\in V \right\}=X\times V $ 가 성립하고 $X\times V\subseteq X\times Y$ 는 $X\times Y$ 에서의 열린집합이 된다.
따름정리($T.P$) 2.12.1)
두 위상공간 $(X,\mathcal{T})$ 와 $(Y,\mathcal{T}')$ 에 대하여, 집합족
$$\mathcal{S}:=\left\{ \pi_1^{-1}(U)=U\times Y\mid U\in\mathcal{T} \right\}\cup
\left\{ \pi_1^{-1}(V)=X\times V\mid V\in\mathcal{T}' \right\} $$ 은 $X\times Y$ 위에서의 곱 위상의 부분기저가 된다.
증명) 비슷한 과정을 따라 $\pi_2$ 에 대해서도 증명 가능하니, $\pi_1$ 에 대해서만 증명한다. 원상(preimage) $\pi_1^{-1}(U)$ 의 정의와 $\pi_1(x,y)=x$ 의 정의에 의해서 관계 $\pi_1^{-1}(U)=\left\{ (x,y)\in X\times Y \mid \pi_1(x,y)=x \in U \right\}=U\times Y$ 는 자명하다. $(x,y)$ 에서 $x$ 는 $U$ 에서 가져오고 $y$ 는 전체 $Y$ 에서 가져오는 것이기 때문이다.
$U\times Y\subseteq X\times Y$ 가 $X\times Y$ 에서 열린집합임을 보이기 위해서는, 가정에 의하여 $U\subseteq X$ 가 $X$ 위에서의 열린집합이라는 것을 떠올리자. 그러면 곱 위상의 정의에 따라 $U\times Y$ 또한 $X\times Y$ 에서의 열린집합이 됨을 알 수 있다. $_\blacksquare$
따름정리의 증명) 주어진 집합족 $\mathcal{S}$ 가 $X\times Y$ 위에서의 곱 위상 $\mathcal{T}_p$ 의 부분기저가 됨을 보이기 위해서는 부분기저원소들의 교집합으로 곱 위상의 기저원소들을 모두 만들 수 있는지를 보이는 것과 같다. 곱 위상의 정의에 의하면, 기저원소들은 $U\times V$ 의 꼴을 가지고 있으며 이때 $U\subseteq X$ 와 $V\subseteq Y$ 는 각각 $X,Y$ 에서의 열린집합이다.
위 정리($T.P$) 2.12) 에 의하여,
$$\begin{align*}
\mathcal{S}&:=\left\{ \pi_1^{-1}(U)=U\times Y\mid U\in\mathcal{T} \right\}\cup
\left\{ \pi_1^{-1}(V)=X\times V\mid V\in\mathcal{T}' \right\}
\\\\&=\left\{ (U\times Y)\cup (X\times V) \right\}
\end{align*}$$
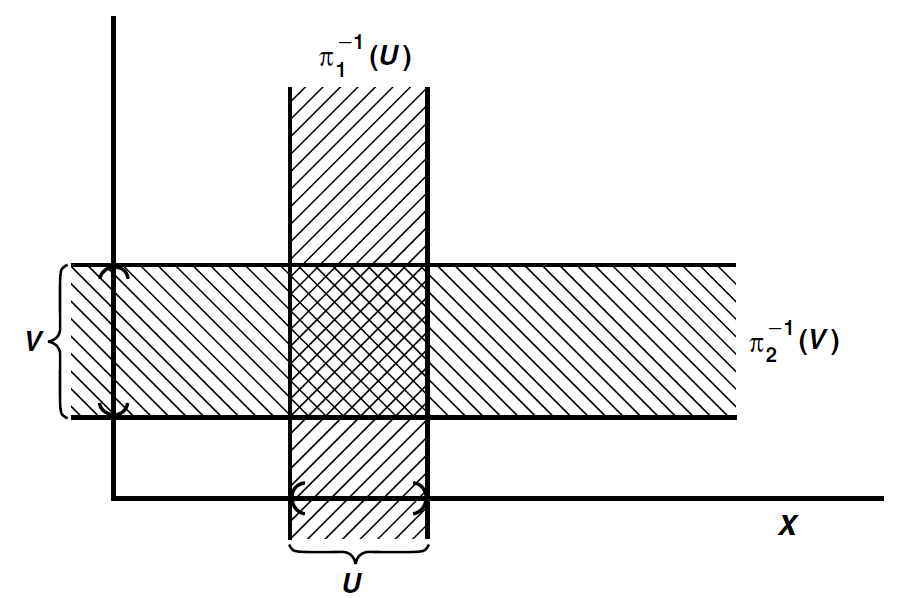
와 같이 쓸 수 있다. 결국 어떤 $U\subseteq X$ 와 $V\subseteq Y$ 가 주어지면, 부분기저원소 $S\in\mathcal{S}$ 는 아래 [그림 2]에서 그려진 십자가 모양의 영역에 포함되는 $(x,y)$ 들을 포함하는 집합이 된다. 이때 두 십자가의 교차 영역인 중간 지역의 점들로 이루어진 집합이 기저원소 $U\times V$ 가 된다. 따라서, $\mathcal{S}$ 의 정의를 보면 두 집합의 합집합 꼴로 되어있는데, 양쪽에서 하나씩 $\pi_1^{-1}(U)=U\times Y$ 와 $\pi_2^{-1}(V)=X\times V$ 를 뽑아 (2개니까 유한) 교집합 시켜서 $U\times V$ 라는 그 어떤 기저원소 $B\in\mathcal{B}$ 도 항상 만들 수 있다. 그러면 그 기저는 곱 위상의 정의에 해당하는 기저이기 때문에, $\mathcal{S}$ 는 부분기저가 된다. $_\blacksquare$
[참고문헌]
James Munkres, Topology 2E
'위상수학(Topology) > 위상공간' 카테고리의 다른 글
| 위상수학에서 닫힌집합(Closed set in topology) (0) | 2024.04.18 |
|---|---|
| 부분공간위상(Subspace topology) (0) | 2024.04.17 |
| 순서위상과 광선(Order topology and ray) (0) | 2024.04.10 |
| 위상수학에서 부분기저(Subbasis for a topology) (1) | 2024.04.07 |
| 위상수학에서 기저(Basis for a Topology) (0) | 2024.03.17 |




댓글