
수학이나 과학 공부를 할 때 가장 중요한 것은 어떤 개념을 학습하는 일입니다. 그런데 우리나라에서는 그 수학적, 과학적개념을 '왜' 배우는 것인지에 대한 학습이 잘 이루어지지 않을 때가 있습니다. 로그가 왜 탄생하였고 쓸모 있는 도구로 각광받았던 것인지, 뉴턴의 2법칙을 운동량과 왜 연결짓는 것인지, 내적은 무엇의 용도로 사용되는지, 자석의 자기장은 전류의 자기장과 어떤 관계가 있을지 등에 관한 것입니다. 뿐만 아니라 어떤 연산이나 행위를 왜 마음껏 사용해도 되는지에 대한 질문에도 학생의 입장에서 좀처럼 답을 구하기 어려운 것들이 있습니다. 예컨대 항등식의 양변에 같은 수를 더하거나 빼도 방정식의 근이 변화하지 않는다는 명제는 군론을 통해 선명하고 깔끔히 증명할 수 있습니다.
상대적으로 대학 전공서적들을 보면 도입부에서 왜 그러한 개념을 배우는지 적어도 중학교, 고등학교 교과서보다는 설명이 자세히 적혀 있습니다. 이유는 후자의 경우 교과서를 보고 해석하는 선생님의 역할이 존재하기 때문입니다. 전자의 경우에도 교수님이 존재하기는 하나 교수는 성취기준이나 교과과정에 맞추어 학생들의 이해도를 점검할 책임이 교사보다는 자유롭다는 점에서 어느 정도 이해할 수 있습니다. 그렇기에 대학교에서 수학 공부를 할 때는 개인적으로 그 개념을 '왜' 배우는지 좀 더 농밀하게 분석해 볼 필요가 있다고 할 수 있습니다.
그렇다면 위상공간은 왜 학습하는 것일까요? 개인적인 생각을 적어 보면 다음과 같습니다. 위상공간은 '공간'이 무엇인지 가장 추상적이고 일반적으로 정의되는 개념입니다. 위상수학을 공부하는 여러분은 적어도 선형대수학에서 벡터공간(Vector space)이 무엇인지 보았을 것이고, 기하학이나 함수해석학 입문에서 놈 공간(norm space)을 본 적이 있을 것이며, 해석학에서 거리공간이나 유클리드공간도 본 적이 있을 것입니다. 이러한 공간들은 사실 부분집합 관계로 촘촘히 이어져 있습니다. 즉 모두 다 따로 노는 개념이 아니고 가장 추상적인 공간인 위상공간에 특별한 성질을 부여해서 더 좁은 개념을 만들어 낸, 톱다운 방식처럼 공간을 직조된 것으로 볼 수 있습니다. 물론, 으레 수학이 그렇듯이 우리는 보통 벡터공간과 같은 특수한 경우를 먼저 배우고, 고급 과목으로 갈수록 점점 추상적이고 넓은 개념을 마주하게 됩니다. 공간의 개념이 발달한 것도 그 방향이기는 합니다. 따라서, 위상공간은 가장 추상적인 공간에 대응되는 것으로, 공간과 관련된 모든 수학에 마인드 맵 그리듯 확장할 수 있습니다. 또한 특수 상대성 이론에서 '시공간'이라는 물리학적 개념이 등장할 때 '공간'이라는 단어를 일상에서처럼 사용하는 것처럼, 위상공간이 주는 이미지는 현실에서의 '공간'과 유사한 점이 굉장히 많기에, 기하학과 뗄 수 없는 밀접한 관련성을 지닙니다. 2016년 노벨 물리학상에서는 '위상부도체'가 등장해 고체물리학과 위상수학의 근사한 접점의 위대함이 공개되면서 또 한 번 세상을 놀라게 했었지요.

따라서 위상수학은 순수학문의 거대한 중추를 담당하는 분야이고, 수학의 큰 세 분야를 대수학, 해석학, 그리고 위상수학 및 기하학으로 나누는 경우가 많습니다. 학부에서는 이 위상수학+미분기하학을 대수와 해석과 동시 또는 이후에 배웁니다. 그만큼 쉽지는 않지만, 최초의 한국계 미국인 필즈상 수상자인 허준이 교수님은 물리학 학부 성적이 매우 저조했으며 거대한 수학적 배경지식이 없었음에도 불구하고 위상수학을 공부하며 수학의 길에 빠져들었다고 인터뷰에서 밝히신 적이 있을만큼 흥미롭기는 합니다. 실제로 위상수학은 집합론 정도의 배경지식만을 요구하고1 대수학이나 해석학의 깊은 이해가 없더라도 나름대로 공부할 수 있으며, 매우 추상적이라는 점에서 계산이 거의 전무하고 고도의 사고력 능력치를 몰빵해서 사용하는, 제가 인정하는 진정한 수학 과목입니다.2 오죽하면 시험도 거의 증명하라는 것만 나옵니다. 이 정도로 소개글을 적으며 하나 하나 쌓아 올린다는 마음가짐으로 또 새로운 관문을 열어 보도록 하겠습니다.
1. 위상과 위상공간
1) 정의
정의($T.P$) 2-1)
집합 $X$ 위에서의 '위상(topology)'이란, 아래의 세 조건을 만족하는 $X$ 의 멱집합 $\mathcal{P}(X)$ 의 한 부분집합족을 말하며 $\mathcal{T}$ 라 표현한다.
① $\emptyset, X \in \mathcal{T}$
② $\mathcal{T}$ 의 임의의 부분집합족의 원소들의 합집합은 $\mathcal{T}$ 에 포함되어 있다 :
$$\displaystyle \bigcup_{\alpha\in I}^{}T_{\alpha} \in \mathcal{T}$$ ③ $\mathcal{T}$ 의 임의의 유한 부분집합족의 교집합은 $\mathcal{T}$ 에 포함되어 있다 :
$$\displaystyle \bigcap_{i=1}^{n}T_{i} \in \mathcal{T}$$ 이때 집합 $X$ 는 '위상공간(Topological space)'라 말하고 $(X,\mathcal{T})$ 라 표기한다.
표기법부터 설명하자면, 위상이 $\mathcal{T}$ 이고 위상공간은 $(X,\mathcal{T})$ 또는 위상이 이미 주어져 혼동의 여지가 없을 때 $X$ 라고 표현하기도 합니다. 즉 $X$ 자체가 위상공간이라는 뜻입니다.
정의를 받아들이고 순수 수학적으로 이해하기 전에, 일단 위상과 위상공간의 개념이 너무 추상적이니 비유를 통해 받아들일 수 있는 설명을 먼저 해보려고 합니다. 위상과 위상공간은 도대체 어떤 개념을 수학적으로 추상화한 것일까요?
처음, 위상공간이라고 이름이 붙는 주어진 집합 $X$ 는 말그대로 어떤 공간이나 집단의 아이디어입니다. 이 공간이나 집단에는, 이를 구성하는 여러 구성원들이 있습니다. 이것이 $X$ 에 들어있는 원소 하나하나의 개념입니다. 이때, 이 원소들이 어떻게 집합 안에서 '연결되어있는지', 얼마나 '근접해있는지'의 연결성과 근접성 개념이 위상의 개념입니다. 즉, 직관적으로 설명해보자면 위상이란 주어진 집합 $X$ 안에서 원소들을 어떻게 '연결'시키고 얼만큼 '가깝게' 위치하게 만들 것인지를 정의하는 규칙이라고 볼 수 있습니다.
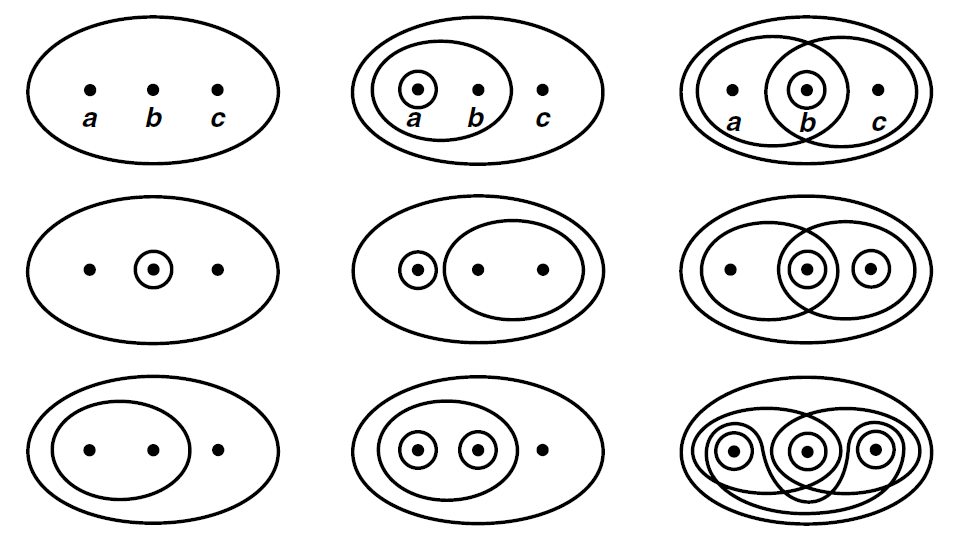
예를 들어 봅시다. 집합 $X=\{ a,b,c\}$ 에 대하여, 아래의 정의($T.P$) 2-3) 에서 소개하겠지만 자명위상(trivial topology or indiscrete topology)라는 것은 $\mathcal{T} = \{ \emptyset, X\}$ 로 정의합니다. 위상에는 오직 공집합과 $X$ 자체만 들어있다는 것이죠. 이것은, 그림으로 따지자면 [그림 3]에서 좌측 최상단에 해당하는, 그냥 $a,b,c$ 세 점이 서로 따로따로 떨어져서 존재할 수 없는 상황에 해당합니다. 이 말은, $X$ 라는 공간 내에 있는 $a,b,c$ 라는 구성원이 각각 따로 분리되어 놓여 있지 못하고 언제나 $X$ 라는 전체 덩어리, 말하자면 일종의 '만남의 광장' 같은 공간에서만 어거지로 보기 싫더라도 얼굴을 보고 지내야만 하는 상태라고 볼 수 있습니다.
더욱 쉽게 비유하자면 다음과 같이 볼 수 있습니다. 타이타닉 같은 유람선을 타다고 조난당해 작은 보트를 타고 망망대해에 떠 있는 같은 보트를 탄 세 사람 $a,b,c$ 가 있다는 것입니다. 여기서는 바다에 빠질 수도 없고, $a$ 라는 사람이 $b,c$ 와 좀 다툰다고 하더라도 이 보트를 떠나면 죽는 것밖에 없으니, 떠날 수가 없겠지요? 어거지로 붙어 있을 수밖에 없다는 것입니다. 이 보트가, 말하자면 원소가 놓여 있을 수 있는 '전체 공간'의 개념인 것이고, 주어진 집합 $X$ 의 의미를 갖는 것입니다. 이게 위상에 들어있는 '$X$' 의 개념입니다.
반면, 8번째 그림을 보도록 합시다(3행 2열에 위치하는 그림). 이 그림이 의미하는 위상은 $\mathcal{T}=\left\{ \emptyset, X, \{ a\}, \{ b\}, \{ a,b\} \right\}$ 입니다. 이는, $a,b$ 라는 두 원소는 마치 자취방같이 독립된 방을 가져서 혼자만의 공간 $\{ a\}, \{ b \}$ 를 가질 수 있고, 카페라는 또다른 공간 $\{ a,b\}$ $c$ 를 따돌리고 만날 수도 있음에 비유할 수 있습니다. 독립적인 공간을 가질 수 있다는 것은 '떨어져 분리될 수 있음'을 의미하므로, 위에서 말한 '근접성'의 개념으로 볼 때는 근접성이 낮은 상태입니다.
그래서 자명위상의 개념은 오직 공집합과 전체집합만이 열린집합이라는 것이라, 모든 점들이 최대한 가깝게 연결되어 있다는 것을 뜻합니다. 각각의 세 원소가 독립된 자취방에 떨어져 살 수 있는 가능성이 없으니깐 말이죠. 반면, $\mathcal{T}=\mathcal{P}(X)$ 라는 이산위상(discrete topology)라는 것도 있는데 이것은 우측 최하단에 놓여 있는 그림에 대응됩니다. 여기서는 모든 점들이 다 떨어져 단일원소로 존재할 수 있으니, 최대한 구성원들이 떨어져 있는 상태로 볼 수 있습니다. 각자 쌩까고 $\{ a\}, \{ b\}, \{ c\}$ 로 존재할 수 있으니까 말이죠.
아래에서 자명위상과 이산위상을 정의하기는 할 것입니다. 하지만 그 전에, 자명위상은 '최대한 점들이 가까운 상태'이고 이산위상은 '최대한 점들이 독립적으로 떨어져 있는 것이 가능한 상태'라고 보시면 됩니다.
이제 수학적인 분석 과정으로 넘어갑시다. 처음 가장 중요한 것은 $U,T\in \mathcal{T}\subseteq\mathcal{P}(X)$ 의 관계를 이해하는 것입니다. 일반적으로 $U,T$ 로 표기하는 것은 $\mathcal{T}$ 의 원소이고 이는 집합입니다. $X$ 역시 집합입니다. 반면 $\mathcal{T}$, $\mathcal{P}(X)$ 들은 집합족에 해당합니다.
①번 조건은 위상은 그 집합 $X$ 자체와 공집합을 원소로 가져야 한다는 것입니다. ②번은 집합족인 위상은 원소를 집합으로 갖게 될텐데, 임의의 위상의 원소들을 어떻게 합집합하더라도 반드시 그 합집합이 위상에 포함되어 있어야 한다는 뜻으로 볼 수 있습니다. 마치 군론에서 합집합이라는 것을 연산으로 본다면 연산의 닫힘성 조건처럼 보입니다. 이때 합집합은 유한집합일수도, 무한집합일수도 있습니다. 마지막으로 ③번 조건은 유한 교집합 조건으로, 교집합은 유한이라는 조건이 달려 있습니다.
그러면 당연히 질문을 던져야 합니다. 합집합은 왜 무한히 허용되고 교집합은 그렇지 않은가에 대해서 말이죠. 3 그런데 일단 지금 수준에서는 이 질문에 대해 100% 명쾌한 답변을 찾기가 어렵습니다. 왜냐하면 그 이유가 열린집합의 정의나 개념에 관련되어 있기 때문입니다. 그렇기 때문에 제 의견은 다음과 같습니다. 우리는 이미 실수(수직선)에서 열린집합의 개념을 학습한 바가 있습니다. 그리고 몇몇 분들은 해석학에서 유클리드 공간에서의 열린집합 개념도 이미 다뤄본 적이 있을 것입니다. 실수에서의 열린집합의 정의에 의하면 주어진 집합이 어떤 무한(또는 유한)한 열린집합의 합집합으로 표현 가능하면 됩니다. $\mathbb{R}=(-\infty,\infty)=\displaystyle \bigcup_{n=1}^{\infty}(-n,n)$ 와 같이 말입니다. 즉, 실수에서 열린구간을 일반화하기 위해 이와 같이 열린집합의 정의를 했습니다. 그리고 이러한 열린집합의 정의는 더욱 추상적인 위상공간에서의 열린집합 정의(앞으로 할 것)과도 잘 부합해야 합니다. 그래서 무한 합집합을 허용하는 것으로 일단 생각하면 좋을 듯 합니다.4 반면 교집합의 개념은 무한 교집합을 하게 되었을 때 열린집합의 성질이 만족되지 않는 경우가 있습니다. 예컨대 실수에서 $0$ 을 중심으로 하고 반지름이 점차 작아지는 모든 열린구간의 교집합은 $\displaystyle \bigcap_{n=1}^{\infty}\left( -\frac{1}{n},\frac{1}{n} \right)$ 와 같이 쓰는데, 결론적으로 이 값은 $\{ 0\}$ 이 됩니다. 그러나 실수(수직선)에서는 이같은 한원소집합은 열린집합이 아니라 닫힌집합입니다.
이처럼, 위상공간의 정의는 열린집합의 정의 그 자체와 붙어 다니는 쌍둥이 관계입니다. 그 까닭은 점차 지식을 쌓아 올리면 계속 해결 가능합니다. 그러면 도대체 열린집합을 어떻게 정의하느냐? 모든 공간을 아우르는 가장 원초적이고 추상적인 공간이 위상공간이고 이 위상공간에서 열린집합의 정의는 아래와 같이 합니다.
정의($T.P$) 2-2) 열린집합(Open set)
위상공간 $(X,\mathcal{T})$ 를 생각하자. 어떤 집합 $T$ 가 '열린집합(Open set)'이라는 것은 $T\subseteq X$ 이고 $T\in\mathcal{T}$ 를 모두 만족한다는 것이다.
쉽게 말해 집합족인 위상 $\mathcal{T}$ 의 모든 원소들을 열린집합이라고 정의합니다. 위상 및 위상공간이라는 조건이 보장되어 있다면, 위상은 언제나 $\mathcal{P}(X)$ 의 부분집합족이기에 위상의 원소들은 반드시 $X$ 에 포함되어 있기 때문입니다. 따라서 우리는 공집합과 $X$ 가 반드시 열린집합이라는 것을 알 수 있습니다.5
예제 1) 집합 $X= \{ a,b,c\}$ 의 한 위상으로 $\mathcal{T}=\left\{ \emptyset \left\{a \right\},\left\{ c \right\},\left\{ a,c \right\}, \left\{ a,b,c \right\}\right\}$ 을 뽑을 수 있다. $\mathcal{T}$ 는 공집합과 $X$ 를 포함하고 있으며 $\mathcal{T}$ 의 임의의 원소를 어떻게 합집합하더라도 $\mathcal{T}$ 안에 여전히 존재한다. 또 유한한 교집합을 만들더라도 그 원소 역시 $\mathcal{T}$ 안에 존재한다. $_\blacksquare$
예제 2) 위상공간 $X$ 에 대해 집합족 $ \left\{ \mathcal{T}_{\alpha}\mid \alpha \in I \right\}$ 을 $X$ 의 가능한 모든 위상들의 집합이라고 하자. 이때
1) $\displaystyle \bigcap_{\alpha\in I}^{}\mathcal{T}_{\alpha}$ 는 $X$ 에서의 위상인가?
2) $\displaystyle \bigcup_{\alpha\in I}^{}\mathcal{T}_{\alpha}$ 는 $X$ 에서의 위상인가?
Sol) 1) 위상의 세 가지 조건을 확인한다.
i) $\emptyset, X$ 는 모든 위상 $\mathcal{T}_{\alpha}$ 에 포함되어 있으므로, $\emptyset, X \in \displaystyle \bigcap_{\alpha\in I}^{}\mathcal{T}_{\alpha}$ 은 자명하다.
ii) 합집합 조건 : 각각의 $U_j \in \displaystyle \bigcap_{\alpha\in I}^{}\mathcal{T}_{\alpha}$ 를 만족하는 집합족 $\{ U_j\}_{j\in J}$ 를 생각하자. 즉 각각의 $U_j$ 는 모든 $\mathcal{T}_{\alpha}$ 에 들어있는 열린집합이다. 그런데 $\mathcal{T}_{\alpha}$ 가 위상이기 때문에, $\displaystyle \bigcup_{j\in J}^{}U_j$ 또한 T2) 에 의하여 모든 $\mathcal{T}_{\alpha}$ 에서 열린집합이다. 따라서 임의의 $\mathcal{T}_{\alpha}$ 에 대해 $\displaystyle \bigcup_{j\in J}^{}U_j \in \mathcal{T}_{\alpha}$ 이므로 $\displaystyle \bigcup_{j\in J}^{}U_j \in \displaystyle \bigcap_{\alpha\in I}^{}\mathcal{T}_{\alpha}$ 가 성립한다.
iii) $\{ U_1,\cdots ,U_n\}$ 을 각각의 $U_j$ 에 대하여 $U_j\in \displaystyle \bigcap_{\alpha\in I}^{}\mathcal{T}_{\alpha}$ 를 만족하는 유한 집합족이라고 하자. 모든 $\mathcal{T}_{\alpha}$ 가 위상이기 때문에, $\displaystyle \bigcap_{j\in J}^{}U_j$ 또한 $\mathcal{T}_{\alpha}$ 에서 열린집합이다. 따라서 임의의 $\mathcal{T}_{\alpha}$ 에 대하여 $\displaystyle \bigcap_{j\in J}^{}U_j \in \mathcal{T}_{\alpha}$ 이므로 $\displaystyle \bigcap_{j\in J}^{}U_j \in \displaystyle \bigcap_{\alpha\in I}^{}\mathcal{T}_{\alpha}$ 가 성립한다. $_\blacksquare$
2) 위상의 세 가지 조건을 확인한다.
i) $\emptyset, X$ 는 모든 위상 $\mathcal{T}_{\alpha}$ 에 포함되어 있으므로, $\emptyset, X \in \displaystyle \bigcup_{\alpha\in I}^{}\mathcal{T}_{\alpha}$ 은 자명하다.
ii) 합집합 조건 : 만족시키지 못한다. $U,V\in \displaystyle \bigcup_{\alpha\in I}^{}\mathcal{T}_{\alpha}$ 으로서 $\beta,\gamma\in I$ 에 대하여 $U\in\mathcal{T}_{\beta}$ 이고 $V\in \mathcal{T}_{\gamma}$ 라고 하자. 그런데 $\beta=\gamma$ 가 아닌 이상, 언제나 $U\cup V\in\mathcal{T}_{\beta}$ 이고 $U\cup V\in\mathcal{T}_{\gamma}$ 라고 단정할 수 없다.
iii) 유한 교집합 조건 : 역시 만족시키지 못한다. 위에서와 비슷하게, $\beta=\gamma$ 가 아닌 이상 $U\cap V\in\mathcal{T}_{\beta}$ 나 $U\cap V\in \mathcal{T}_{\gamma}$ 가 성립한다고 단정할 수 없다.
따라서 $\displaystyle \bigcup_{\alpha\in I}^{}\mathcal{T}_{\alpha}$ 는 $X$ 에서의 위상이 아니다. $_\blacksquare$
정의($T.P$) 2-3) 여러가지 위상공간들
집합 $X$ 가 주어졌다고 하자. $X$ 는 임의의 집합으로 가져야 할 특별한 조건이 없다.
① $\mathcal{T}_d:=\mathcal{P}(X)$, 즉 $X$ 의 모든 부분집합들로 이루어진 멱집합을 집합 $X$ 위에서의 '이산위상(discrete topology)'이라고 한다. 반면 $\mathcal{T}_t:=\left\{ \emptyset ,X \right\}$ 는 '자명위상(trivial topology)' 또는 '비이산위상(indiscrete topology)'라 한다.
② 집합 $X$ 위에서의 '유한여위상(finite complement topology)'6 $\mathcal{T}_f$ 란 원소가 $\emptyset$ 이거나 $X-U$ 를 유한집합으로 만드는 $U$ 로 이루어진 위상을 말한다. 조건제시법으로 쓰면,
$$\mathcal{T}_f:=\left\{ \emptyset \right\}\cup \left\{ U\subseteq X\mid X-U \text{ is finite} \right\}$$
③ 집합 $X$ 위에서의 '가산여위상(countable complement topology)' $\mathcal{T}_c$ 란 원소가 $\emptyset$ 이거나 $X-U$ 를 가산집합으로 만드는 $U$ 들로 이루어진 위상을 말한다. 조건제시법으로 쓰면,
$$\mathcal{T}_c:=\left\{ \emptyset \right\}\cup \left\{ U\subseteq X\mid X-U \text{ is countable} \right\}$$
정의를 보면 유한여위상이나 가산여위상은 $X$ 가 유한집합일 때는 그냥 $\mathcal{T}_f=\mathcal{T}_c=\mathcal{P}(X)$ 입니다. 그러니 보통 이들은 $X$ 가 무한집합일 때 많이 등장합니다.
일단 유한여위상과 가산여위상을 저렇게 정의한다는 뜻이긴 하나, 실제로 위상공간이 되는지는 검증을 해볼 필요가 있을 것입니다. 아래 예제를 통해 검토해 보겠습니다.
예제 4) $\mathcal{T}_f$ 을 위에서와 같이 정의하면 이것이 위상공간인지 보여라.
Sol) 첨수집합족(indexed famil) $\{ U_{\alpha} \}$ 가 공집합이 아닌 $\mathcal{T}_f$ 의 원소일 때, 그리고 $\alpha\in I$ 가 각각 첨수와 첨수집합일 때, $\displaystyle \bigcup_{\alpha \in I}^{} U_{\alpha}\in \mathcal{T}_f $ 를 보이고, 또 유한집합 $\{ U_i\mid 1\leq i \leq n,\; i,n\in\mathbb{N} \}$ 에 대하여 $\displaystyle \bigcap_{i=1}^{n}U_{i} \in \mathcal{T}$ 가 만족되는지를 보이면 된다.
i) $\emptyset,X\in\mathcal{T}$ 는 자명하다.
ii) 집합족에 대한 드 모르간의 법칙을 쓰면,
$$\begin{align*}
X-\displaystyle \bigcup_{\alpha \in I}^{} U_{\alpha}&= X\cap \left( \displaystyle \bigcup_{\alpha \in I}^{} U_{\alpha} \right)^c =X\cap \left( \displaystyle \bigcap_{\alpha \in I}^{} U^c_{\alpha} \right)
\\\\&= \displaystyle \bigcap_{\alpha \in I}^{} \left( X\cap U_{\alpha}^c \right)=
\displaystyle \bigcap_{\alpha \in I}\left( X-U_\alpha \right)
\end{align*}$$
가 성립한다. 그런데 각각의 $U_{\alpha}\in \mathcal{T}_f$ 라는 가정으로 인해 각각의 $X-U_{\alpha} $ 또한 유한하다. 고로 교집합 $\displaystyle \bigcap_{\alpha \in I}\left( X-U_\alpha \right)$ 또한 유한하여, $\displaystyle \bigcup_{\alpha \in I}^{}U_{\alpha}\in \mathcal{T}_f $ 가 성립한다.
iii) 비슷한 방식으로
$$\begin{align*}
X-\displaystyle \bigcap_{i=1}^{n}U_{i} &= X\cap \left( \displaystyle \bigcap_{i=1}^{n}U_{i} \right)^c
=X\cap \left( \displaystyle \bigcup_{i=1}^{n}U_{i}^c \right)
\\\\&= \displaystyle \bigcup_{i=1}^{n} \left( X\cap U_i^c \right)=
\displaystyle \bigcup_{i=1}^{n}\left( X-U_{i} \right)
\end{align*}$$
인데, 가정의 의해 각각의 $X-U_i$ 는 유한하다. 따라서 $\displaystyle \bigcap_{i=1}^{n}U_{i} \in \mathcal{T} $ 이다. $_\blacksquare$
예제 5) $\mathcal{T}_c$ 는 위상공간인지 확인해보아라. 예제 2)와 비슷한 방법을 쓰면 된다.
i) $\emptyset, X\in\mathcal{T}$ 가 성립한다.
ii) 집합족에 대한 드 모르간의 법칙을 적용하면 $X-\displaystyle \bigcup_{\alpha \in I}^{} U_{\alpha}=\displaystyle \bigcap_{\alpha \in I}\left( X-U_\alpha \right)$ 가 된다. 가정에 의해 각각의 $X-U_{\alpha}$ 는 가산집합이다. 그러면 가산집합들의 가산집합은 가산집합의 부분집합으로, 따름정리($S.T$) 4.10.1) 에 의하여 가산집합들의 교집합은 가산집합이다.
iii) 비슷한 방식으로 $X-\displaystyle \bigcap_{i=1}^{n}U_{i}=\displaystyle \bigcup_{i=1}^{n}\left( X-U_{i} \right)$ 가 성립하고, 여기서 각각의 $X-U_i$ 들은 모두 가산집합이다. 따름정리($S.T$) 4.11.1) 에 의해 가산집합의 (유한)합집합도 가산집합이다.
이로부터 가산여위상 $\mathcal{T}_c$ 는 위상공간이다. $_\blacksquare$
2) 부분집합 관계
정의($T.P$) 2-4) 세밀함과 성김(finer and coarser)
주어진 집합 $X$ 위에서의 두 위상공간 $\mathcal{T},\mathcal{T}'$ 에 대하여,
① $\mathcal{T}'$ 가 $\mathcal{T}$ 에 비해 '(더)7 세밀하다(finer)'는 것은 $\mathcal{T}\subseteq \mathcal{T}'$ 인 것과 필요충분조건이다.
만일 부분집합 관계가 진 부분집합 관계이면, $\mathcal{T}'$ 는 $\mathcal{T}$ 에 비해 '(더) 강하게 세밀하다(Strictly finer)'고 한다.
② $\mathcal{T}$ 가 $\mathcal{T}'$ 에 비해 '(더) 엉성하다(finer)'는 것은 $\mathcal{T}\subseteq \mathcal{T}'$ 인 것과 필요충분조건이다.
만일 부분집합 관계가 진 부분집합 관계이면, $\mathcal{T}$ 는 $\mathcal{T}'$ 에 비해 '(더) 강하게 엉성하다(Strictly finer)'고 한다.
영어에서 'coarser'은 더 '굵은' 또는 '거친' 정도의 의미를 가집니다. 하지만 저는 그것의 번역을 '성긴', '엉성한' 정도로 하는 것이 적당하다고 봅니다. 전자의 두 단어는 말하자면 촉감이고, 후자의 제 번역은 시각입니다. 즉 시각의 개념으로 보는 것이 맞다고 생각한다는 것입니다. 이는 $\mathcal{T}'$ 을 조금 더 잘게 쪼개서 간격이 세밀해진 것이 $\mathcal{T}$ 의 개념이므로, 쪼개기 전 간격이 더 넓다는 것을 의미하기 위해서는 엉성하다라는 시각적 관점이 직관에 더 들어맞기 때문입니다.
[참고문헌]
James Munkres, Topology 2E
- 집합론을 모른다면 위상수학 공부가 난해합니다. 집합족의 개념, 기수의 개념, 가산집합, 그리고 선택공리에서 유도되는 나머지 3가지 명제의 개념 정도를 필수로 알고 있어야 합니다. 대부분 블로그에 다 이미 올려 두었습니다. [본문으로]
- 물론 주인장은 대수학을 제일 좋아합니다. 아주 '적당한' 수준의 계산이 더해져 대부분은 논리+사고로 떡칠된 과목이니까요. 그리고 일상에의 응용과 적용이 나름대로 가능하다 생각할 뿐만 아니라, 경이롭습니다. [본문으로]
- 제가 몇몇 글에서 자주 강조하는 것이, 수학에서 '정의'는 받아들여야 하는 것은 맞지만 그래도 '왜 이따구로 정의를 할까?'에 대해 한번쯤 고민해보는 것이 좋습니다. 물론 이러한 고민은 때때로 쓸데없어 보이기도 하고, 시간낭비라고 생각하는 분들도 있습니다. 하지만 단언컨데 정의는 수학자들이 누구나 합의할 수 있는 방향으로 엄밀히 쌓아 올린 약속이고, 수많은 수학자들이 끊임없이 고민해서 빚어낸 결과물입니다. 그러니 당시 수학자들이 어떤 고민을 했었던 것인지 한 번쯤 탐구해보는 것은 절대로 쓸모없는 고민이 아닙니다.이러한 접근법에 대한 예시로, 기수의 거듭제곱 글에서 제가 왜 기수의 거듭제곱을 그따위로 정의하는지 설명한 바가 있습니다. [본문으로]
- 완전한 의문의 해결은 계속 공부를 하다 보면 알 수 있을 것입니다. [본문으로]
- 지금 공집합과 $X$ 가 왜 열린집합인지를 깊게 탐구하는 것보다는, 일단 이렇게 정의했을 때 계속 공부를 하다 보면 우리가 아는 그 직관적인 열린집합의 개념과 나중에 연결된다는 사실을 믿고 나아가는 것이 좋을 듯 합니다. [본문으로]
- '여유한위상'으로 번역하는 교재도 있습니다. [본문으로]
- 비교급이니까 당연히 '더'를 붙이는 것이 맞기는 하지만 단순히 세밀하다고 말할 수도 있으니 참고해 주시기 바랍니다. [본문으로]
'위상수학(Topology) > 위상공간' 카테고리의 다른 글
| 부분공간위상(Subspace topology) (0) | 2024.04.17 |
|---|---|
| 곱 위상(Product topology) (0) | 2024.04.13 |
| 순서위상과 광선(Order topology and ray) (0) | 2024.04.10 |
| 위상수학에서 부분기저(Subbasis for a topology) (1) | 2024.04.07 |
| 위상수학에서 기저(Basis for a Topology) (0) | 2024.03.17 |




댓글