* 이 글은 1탄이며, 이후 2탄과 이어집니다.
* 이 글에 대한 방문객이 급증하고 있는데, 단순히 테일러 공식을 찾고 싶으시면 스크롤을 조금만 내려 공식을 확인할 수 있습니다. 하지만 이 글의 목적은 테일러 급수 및 전개를 이해하는 것이라 충분한 시간과 노력 없이 얼렁뚱땅 읽을 필요는 없습니다.
* 지금부터 시작할 테일러 급수에 관한 논리 전개는 상당히 어렵습니다. 고난도 수학을 깨부수는 유일한 방법은 오로지 '끝까지 포기하지 않고 고민하기'라는 스킬을 장착하는 것입니다. 그렇지 않으면 이 글은 쓸모가 없음을 반드시 명심하고 들어오시길 권하겠습니다.
1. Introduction
대학에 입학한 자연계 학생이면 아주 적은 예외를 논외하고 반드시 미적분학을 1학년 때 수강해야 합니다. 미적분학을 처음 배우게 되면 엡실론-델타 논법을 제외하고는 고등학교 수학과 별다른 내용이 등장하진 않습니다. (22학번부터는 미적분을 선택하지 않았다면 고생할 수도 있겠군요... 그러나 기하를 선택하지 않은 만큼 나중에 벡터 파트가 나올 때 고생하게 되니 미적분 선택이나 기하 선택이나 미적분학 유불리 관점에서는 차이가 없다고 봅니다.)
그러다가 급수 판정법에 가서야 드디어 새로 배우는 내용들이 하나 둘 등장하고, 1학기의 종강은 테일러 전개, 테일러 급수와 동행할 가능성이 높습니다. 저에게 만약 누가 (고등학교에서 배우는 개념을 제외한) 미적분학에서 가장 중요한 개념을 3가지 뽑으라고 한다면 테일러 급수, 발산정리, 스토크스 정리라고 말할 것입니다.
그런데 아주 높은 확률로 미적분학을 수강할 때는 기초과목이며 고등학생 공부법을 그대로 적용하다 보니 대학이라는 위상에 걸맞지 않게 심도있는 깊이로 이해를 하지 못하는 경우가 다반사입니다. 뭐 물론 한창 술퍼먹어야 할 학년이기도 하기에 더욱 미적분학은 단순 고등수학의 연장선으로만 바라보는 경우가 많습니다. 그런데 위 3가지 개념은 1학년 때 제대로 다져 두지 않으면 공업수학, 수리물리, 해석학 등에 가서 다시 배울 수 있기는 해도 피를 보기 아주 좋습니다. 시도 때도 없이 저들은 우리에게 동시공격을 퍼붓기 때문이죠.
3가지 중 하나인 테일러 급수의 경우 저는 미적분학의 최고봉이자 꽃이라 단언할 수 있습니다. 그러나 이를 심층적으로 이해하기에 너무 많은 시간이 걸리며 내용 자체의 난이도가 상당히 높습니다. 그래서 암기식으로 대충 정리하고 넘어가는 분들을 위해 각종 궁금증을 모두 해결할 수 있도록 자세히 포스팅하려고 합니다. 참고로 글을 쓰고 있는 저도 미적분학을 처음 배울때 당연히 단번히 이해하지 못했고, 몇 년에 걸쳐 누적된 시간 속에 공들여 이해하기에 다르렀습니다. 아마 저와 같이 1학년이 아닌 분들이 더 많이 이 글을 읽고 계실 거라 믿습니다. 한 번 시작해 봅시다.
2. 테일러 전개
1) 우리가 뽑아낼 결과는 초록명제다.
테일러 급수에 관한 논의에서 가장 마지막에 해결해야 할 것, 그리고 모든 개념을 관통는 가장 중요한 명제는 다음과 같습니다. 그리고 앞으로 '초록명제'라 부르겠습니다.
'어떤 함수 f(x)를 어떤 조건·상황 속에서 급수 형태로 전개할 수 있는가?'
미리 말하자면 테일러 급수의 표현이나 테일러 전개는 아무때나 써먹는 것이 아니라, 분명히 그것을 사용할 수 있는 특별한 조건이 존재합니다. 그러나 우리는 막연하게 단순히 공식만을 사용해 주어진 함수를 1번미분, 2번미분, 3번미분하고 그것을 계수로 단 다음 x의 거듭제곱을 붙여 시그마로 표현하기만 했었죠. 사실 학부 미적분학 수준에서는 이런 방식으로 얼렁뚱땅 테일러 급수를 이해해도 아마 시험에서 큰 불이익이 존재하진 않을 것 같습니다. 그렇지만 이 글에서는 왜 그런 일이 가능한지 자세히 알아볼 것입니다.
2) 테일러 급수와 테일러 전개의 정의
정리(CC) 2.1
무한번 미분가능한 어떤 함수 f(x)가 존재한다고 하자. 이 함수의 'x=a 에서의 테일러 급수(Taylor Series)'란 다음과 같이 계수를 fn(a)n! 으로 하는 (x−a)n(n=0,1,2,⋯) 의 다항식들의 합으로 표현되는 급수이다.
f(x)=f(a)+f′(a)(x−a)+f″(a)2!(x−a)2+⋯f(n)(a)n!(x−a)n+⋯ 이와 같이 함수를 테일러 급수로 나타내는 방법을 '테일러 전개(Taylor Expansion)'이라고 부른다. 특별히 a=0인 테일러 급수는 '맥클로린 급수(Maclaurin series)'라 한다.
위 박스 내용을 정확히 읽었다면, 테일러 전개를 할 수 있는 경우가 언제인지, 그리고 테일러 급수가 존재할 조건은 무엇인지 대답을 할 수 있게 됩니다. 그것은 바로 주어진 함수 f가 무한번 미분가능한 함수여야 한다는 것입니다. 왜냐하면 만일 f(x)가 무한번 미분 가능하다면, 모든 실수 x에 대해 (따라서 x=a일 때도) f′(x),f″(x),⋯fn(x) 가 반드시 존재한다는 뜻이기 때문이죠. 하지만 많은 경우 우리는 테일러 전개를 사용하고 그것이 매끄럽게 f(x) 를 나타내는 것이라고 알고 있으며 기계적으로 공식을 사용할 뿐입니다.
그런데 근본적인 질문을 던져봅시다. 나중에 배우게 될 지수함수에 관한 테일러 급수 표현은
ex=∞∑n=0xnn!=1+x+x22!+x33!+⋯
입니다. 그런데 의심이 가지 않습니까? 지수함수를 어떻게 다항함수의 합으로, 그것도 '무한히 많은 항'을 더해서 얻어낸단 말입니까? 논리의 끝판왕 과목 수학에서 이런 어거지같은 공식을 두고 우연히 지나친다면 수학을 잘한다고 보기 어렵습니다. 말도 안되는 일에 펄쩍 뛸 자세가 갖추어져 있어야 정확한 수학 공부를 하고 있는 것입니다. 그러니 저는 다음과 같은 질문을 던집니다.
테일러 급수 공식은 항상 사용할 수 있을까요?
∗아닙니다. 정확히 말하자면, 무한히 미분 가능하다면 '테일러 전개' 자체는 언제든지 할 수 있지만, 그 테일러 전개를 한 식이 진짜 f(x) 와 같다는 보장1을 하기 위해서는 추가적인 조건이 필요합니다. 즉, 테일러 급수는 '멱급수 표현식'과 같을 수도 있고, 같지 않을 수도 있습니다. 잠깐, f(x)가 '멱급수 표현식'이 된다는 것은 무슨 뜻이냐하면
f(x)=∞∑n=0an(x−a)n
을 말하는 것입니다. 주의할 것이 테일러 급수도 멱급수는 맞지만, 여기서 제가 말한 '멱급수 표현식'이란 테일러 전개를 이용하지 않고 f(x) 를 멱급수로 나타낼 수 있을 때의 표현식을 가리키는 것입니다.
여기서 테일러 급수가 멱급수 표현식과 같아지는 경우가 우리가 맨날 썼던 ex,sinx 등을 다항함수로 나열하는 공식을 쓸 수 있는 안전한 경우입니다. 그러나, 테일러 급수가 멱급수 표현식과 달라 테일러 공식을 사용할 수 없는 경우도 있습니다. 그건 무슨 뜻이냐하면 예컨대 테일러 전개식의 세번째 항의 계수는 f″(a)2! 이죠? 이게 f(x)를 실제 멱급수 표현식으로 전개했을 때 a3와 같지 않을 수 있다는 겁니다. 그러면 테일러 전개는 이 때 아무 쓸모가 없는 셈입니다.
<2022.7.12 부로 여기까지의 글 내용 중 표현의 정확도를 높이고자 일부 수정했습니다. 아래의 갈색 내용은 수정 전 표현의 모호함이 존재했고 그에 대한 오해를 방지하고자 쓴 설명입니다. 2022.7.12 이후 시점에 글을 읽으시는 분들은 갈색 내용을 읽으실 필요가 없습니다.>
∗ 그런데 여기서 자연스럽게 드는 의문이 있습니다. 테일러 급수도 분명 x에 관한 다항식들을 가지고 있는데 멱급수가 아니라는게 무슨 뜻일까요?
테일러 급수는 반드시 x의 거듭제곱꼴을 가지고 있는 급수이므로 테일러 급수이면 멱급수라는 명제는 참입니다. 즉 테일러 급수의 집합 ⊑ 멱급수의 집합이라 할 수 있습니다. 그럼에도 불구하고 제가 위의 붉은색 표현을 한 것은 나름의 까닭이 있습니다. 지금 이것을 이번 포스팅에서 전부 설명할 수는 없습니다. 고로 위의 붉은 문장을 포함하여 여기서 '멱급수'라고 부르는 것은 일반적인 멱급수의 정의가 아니라, 아래 예제 1)에서 등비급수의 수렴 공식 등을 이용해 전개한 멱급수를 말하는 것입니다. 정확히 말하자면 주어진 함수 f(x)로 수렴하는 테일러 급수입니다. (그러나 이 밑줄 친 말을 처음 공부하시는 분들은 무슨 뜻인지 모를테니 계속 다음 글까지 전진하시면 됩니다.) 여기에는 대체용어가 없어서 일단 이렇게 억지로라도 표현을 바꾸겠다는 것입니다. 나중에 가면 이 멱급수=테일러 급수가 같아지는 상황은 주어진 함수가 테일러 급수로 수렴하는 경우(=일반적인 경우의 해석함수)를 말합니다.
예제 1) 함수 11−x 의 테일러 급수와 멱급수 표현은 서로 같은가? 다시 말해 테일러 전개가 쓸모 있는가?
예제의 목적은 '멱급수 표현식'과 '테일러 급수'를 구하는 방식이 원칙적으로 다름을 설명하는 것에 있습니다. 이 함수는 워낙 유명해서 멱급수 표현을 찾으려면 무한등비급수의 수렴 공식을 쓰면 됩니다. −1<x<1 에서, 멱급수는
11−x=1+x+x2+x3+⋯+xn+⋯
입니다. 누차 말하지만 이건 멱급수 표현식입니다. 그리고 정확한 멱급수를 구하는 건 지금 한 것처럼 테일러 전개를 몰라도(안쓰고) 할 수 있지요. 반면 테일러 급수를 구하려면 분수함수의 미분을 겁나 하여
(11−x)′=1(1−x)2,(11−x)″=2(1−x)3,(11−x)(3)=6(1−x4)
를 얻은 다음 쓸 수 있습니다. x=0 에서의 테일러 급수는
11−x=11−0+1(1−0)2x+22!(1−x)3x2+63!(1−x4)x3=1+x+x2+x3+⋯
따라서 이 함수는 테일러 급수 = 멱급수임을 증명했습니다. 단, −1<x<1 에서만이죠!! 이 범위를 제외하고서는 테일러 급수는 존재하지만 멱급수는 존재하지 않습니다. 다시 말해, 주어진 범위가 x≤−1,x≥1 이면 테일러 급수와 멱급수 표현식은 다른 것입니다. 이 범위를 제외하고서는 f(x) 가 멱급수 표현식으로 쓰여지지 못합니다. 등비급수의 발산 영역이니까요.. 하지만 f(x) 는 미분 가능하므로 주어진 범위 바깥에서도 테일러 전개 자체를 할 수는 있다는 겁니다. 하지만 전개를 해봤자 그건 f(x)를 나타내는 식이 아니겠죠? 그러니 엉뚱한 범위에선 테일러 전개를 해봤자 쓸모가 없다는 것입니다.
예제 2) 함수 f(x)={0(x=0)e−1x2(x≠0)
는 x=0 에서의 테일러 급수(맥클로린 급수)와 멱급수 표현식이 다른 함수이다. 이를 보여라.
우선, 이 함수의 멱급수 표현은 당장 할 수 없습니다. 우리가 배운 멱급수 표현이 가능한 함수는 고작 등비급수였는데, 갑자기 초월함수가 나왔고 초월함수의 멱급수 표현법은 아직 배우지 않았습니다. 그러니 그냥
f(x)=e−1x2=∞∑n=0anxn
라고 뭔가 멱급수 표현이 된다고 가정을 해봅시다. 그리고 테일러 전개를 해보겠습니다. 당연히 x=0 일 때는 할 필요가 없고, x≠0 일 때 미분을 해야 하는데(울프림 알파 돌립시다), 해보니까 a=0에서는
f′(0)=(−2a2√ea3)a=0
이렇게 나옵니다. 도함수를 포함하여 이계도, 삼계도함수도 다 x=0에서 분모가 0이 되니 미분계수를 구하려면 미분계수의 정의인 극한식을 써야 합니다. 아래와 같이 계산하고 마지막에 로피탈의 정리를 몇 번 썼습니다.
f′(0)=lim
다 해보면 알겠지만 f'(0)=f''(0)=\cdots =f^{n}(0)=0 이 나옵니다! 따라서 x\neq 0 일 때 이 함수의 테일러 급수는
f(x)=f(0)+f'(0)\,x+\frac{f''(0)}{2!}\,x^2+\cdots \frac{f^{(n)}(0)}{n!} \,x^n +\cdots=0\neq e^{-\displaystyle\frac{1}{x^2}}
그러니 테일러 급수는 x\neq 0 인 구간에서 절대로 멱급수 표현식(이 있다고 가정한 상태임)이랑 같을 수가 없습니다. 왜냐? 멱급수 표현식은 일단 있다면 반드시 f(x)와 같습니다. 근데 테일러 급수가 f(x)와 다르니까 멱급수 표현식이 테일러 급수가 다르다는 삼단논법을 쓴 것입니다. (a=b 이고 b\neq c 이므로 c\neq a 이다)
이해가 되셨나요? 그러니까 무한번 미분 가능한 함수는 우선 테일러 전개를 해서 테일러 급수를 얻을 수 있을 뿐이지, 진짜 우리가 찾고자 하는 함수 f(x) 와 같다는 보장을 항상 할 수가 없다는 뜻입니다. 다시 말해 어떤 함수가 (테일러 전개가 아닌 다른 방법으로) 멱급수 표현식이 가능하다 하였을 때, 그러한 함수의 집합은 단순히 무한번 미분가능한 함수(=테일러 전개할 수 있는 함수)의 집합과 같지 않습니다. 테일러 전개는 미분 가능한 함수 전체에 대하여 할 수 있지만, 멱급수로 표현 가능한 함수는 거기에 추가로 몇가지 조건을 더 만족해야 합니다. 그 조건이 무엇인지는 2탄에서 계속될 것입니다. 이 관계를 벤다이어그램으로 그리자면
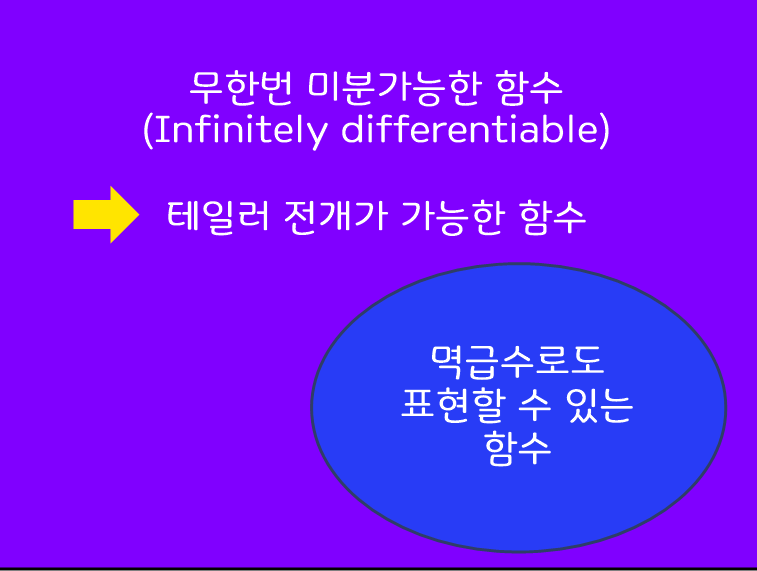
와 같습니다.
3) 멱급수 표현식과 테일러 급수가 같은 경우
그런데, 실제로 멱급수 표현식은 항상 테일러 전개식과 결과가 같습니다. 그를 보여주는 정리를 증명할 것입니다. 아니, 분명 예제 2)에서는 그러지 않을 수도 있다고 하지 않았냐고 반문할 수 있을텐데요. 실제로 f(x) 라는 함수가 테일러 전개를 했을 때 정말 f(x) 와 같지 않은 경우에는, f(x) 의 멱급수 표현 자체가 존재하지 않는 경우랍니다. 그래서 예제 2)를 풀 때는 f(x) 의 멱급수 표현이 일단 있다고 가정을 한 겁니다. 근데 아래의 정리 2.2를 보고 나면, 애초에 그런 가정이 잘못되었음을 알 수 있습니다.
정리(CC) 2.2
함수 f(x) 를 x=a 근방에서 다음과 같이 a가 중심인 멱급수로 나타내어진다고 하자. 곧
f(x)=\sum_{n=0}^{\infty}a_n\left ( x-a \right )^n=a_0+a_1\left ( x-a \right )+a_2\left ( x-a \right )^2+ \cdots +a_n\left ( x-a \right )^n+\cdots
이라는 뜻이다. 그러면 반드시 계수는 a_n=\displaystyle\frac{f^{n}(a)}{n!} 으로 주어진다.
증명) 위 식의 양변을 계속 미분해보자.
\begin{align*} &f(x)=a_0+a_1\left ( x-a \right )+a_2\left ( x-a \right )^2+a_3\left ( x-a \right )^3+ \cdots \\\\& f'(x)=a_1+2a_2\left ( x-a \right )+3a_3\left ( x-a \right )^2+ \cdots \\\\& f''(x)=2!a_2+3!a_3\left ( x-a \right )+4\cdot 3c_4\left ( x-a \right )^2+ \cdots \\\\& \end{align*}
여기서 x=a 를 대입하고, a_n 에 대해서 정리하면 다음을 얻는다.
a_0=f(a) \;\;, \;\; a_1=f'(a) \;\;,\;\; a_2=\frac{f''(a)}{2!} \;\;,\;\;a_3=\frac{f''(a)}{3!}
따라서 모든 자연수 n에 대해 a_n=\displaystyle\frac{f^{n}(a)}{n!} 이 성립한다.
4) 언제 멱급수와 테일러 급수가 같은가?
그러면 도대체 어떤 조건에서 주어진 함수 f(x)가 테일러 급수가 같은 것인지에 대한 의문이 들지 않을 수 없고, 이에 대한 해답이 초록명제의 정확한 답이라 할 수 있습니다. 결론부터 말하자면 라그랑주의 나머지항의 극한값이 0으로 가면 됩니다. 이 말을 이해하려면 테일러 공식, 테일러 정리, 라그랑주의 나머지항에 대한 이해를 끝마쳐야 합니다. 이 내용들은 다음 2탄에 모두 소개되어 있습니다. 다만 다음 포스팅을 읽기 전에 평균값의 정리를 상기하시길 권장드립니다.
- 위에서 언급한 지수함수는 이 보장이 이미 되어 있는 일종의 안전한 함수이기 때문에 우리가 별 걱정 없이 테일러 전개를 마구잡이로 할 수 있는 정예 함수입니다. 이런 '보장'이 무엇인지는 글을 읽다 보면 2탄에서 밝혀집니다. [본문으로]
'미적분학(Calculus) > 급수' 카테고리의 다른 글
| 테일러 급수와 해석함수 (Analytic function with Taylor series) (7) | 2021.01.17 |
|---|---|
| 테일러 정리와 테일러 공식 (Taylor's Theorem and Taylor's Formula) (5) | 2021.01.17 |
| 멱급수의 연산 및 항별 미분과 적분에 관한 성질 (Operations on Power seires, Term-by-term Differentiation and Integration) (0) | 2021.01.16 |
| 멱급수, 거듭제곱급수와 수렴집합 (Power series and its Convergence Test) (0) | 2021.01.16 |
| 비판정법, 절대 비판정법 (Ratio Test, Absolute Ration Test) (0) | 2021.01.16 |



댓글