행렬과 선형변환의 동형 관계 성질(The Isomorphic relation between Matrix and Linear Transformation)

이제 행렬과 선형변환의 세계를 대응시켜 보면서 두 세계의 유사성을 파악할 시간입니다. 이 내용은 모든 선형대수학 책에 사각형 형태로 기술되어 있기도 하고, 책에 따라 선형대수학의 기본정리라는 거창한 말을 붙이기까지 할 정도로 심도있고 강조해서 다루어야 하기 때문에, 조금 길게 서론을 작성해 보겠습니다.

---

1. 개요

 

동형(isomorphic)이라는 말을 다시 한번 떠올려 봅시다. 영어보다는 한자를 생각하면, 한가지·같을 동(同)에 모양·거푸집 형(型)을 씁니다. 직역하면 형태가 동일하다는 뜻이죠.

 

'(무엇과 무엇의)형태가 동일하다'는 말은 '(무엇과 무엇이)완전히 동일하다'는 말과는 다릅니다. 후자의 개념은 'A는 A다'처럼 사실은 같은 대상인데, 그를 가리키는 단어가 둘 이상인 경우를 말합니다. 마치 '총각은 결혼하지 않은 남성이다'처럼 동어 반복 명제가 바로 그 예입니다. 반면, 형태가 동일하다는 말은 서로 다른 두 대상에 대해서도 말할 수 있습니다. 예컨대 'A와 B의 형태가 동일하다'라고 한다고 해서 'A와 B가 동일하다'를 뜻하는 것은 아닙니다. 역은 성립하겠지만요.

 

비트겐슈타인의 전기 철학을 대표하는 <논리철학논고>를 보면 '그림 이론' ^[각주:1]이라는 것이 등장합니다. 비트겐슈타인은 어느 날 프랑스의 한 법정에서 교통사고 장면을 묘사하기 위해 장난감 자동차와 인형을 사용했다는 내용이 실린 신문 기사를 읽게 됩니다. 법정에서 모형 자동차와 인형이, 실제 사고의 자동차와 사람을 모델로 하여 법정의 사람들에게 당시 상황을 실감나게 이해시켜주었다는 것이죠. 이와 같은 모델을 토대로 그는 언어가 세계에 대한 그림으로, 언어는 세계에, (복합)명제는 (복합)사실에 대응되는 관계가 있음을 주장합니다.

 

동형이 가리키는 것은 바로 이런 것입니다. 언어와 세계가 동어 반복 명제처럼 완전히 같은 대상은 아닙니다. 곧, '언어는 세계다'라는 명제는 거짓입니다. 하지만 '언어는 세계와 대응된다'라는 명제는 참인데, 이는 언어와 세계의 형태가 동일하다는 말을 내포합니다. 간단히, 그림으로 나타내면 다음과 같습니다.

 

 

두 집합의 대상을 일대일 대응시킬 수 있을 때, 그 일대일 대응 하는 작업이 바로 함수(=사상=변환)을 만들어내는 방법이며 이러한 상황을 가역이라 부르고, 그 때 두 집합이 동형 관계라고 말하는 것입니다. 그러면 이제 동형의 개념을 최소한 직관적으로라도 이해할 수 있을 겁니다. 쉽게 말해 두 대상이 '그게 그거다' 라고 받아들이는 것이 가장 좋습니다.

 

다만 우리는 지금 벡터공간을 다루고 있는 상황이기 때문에, 그 집합이 연산이 가능하다는 조건을 더 필요로 합니다. 예컨대 지금 위에 제가 만든 언어와 세계라는 집합은 그 안에서 벡터의 합과 스칼라 곱이 보존되는 성질을 만족하지는 않기 때문에 벡터공간은 아닙니다.

 

그렇다면 이런 연산까지 가능한 예시를 만들 수 있을까요? 예를 들어 미국의 1달러(1$\$$)가 1200원(\1200)으로 고정 환율제가 운영된다고 생각해봅시다. 그러면, 

 

$$1 \;\mathrm{dollar}=1200 \;\mathrm{won}$$

 

이라고 쓸 수 있습니다. 여기서 등호는 실제 세상에서 1달러랑 1200원이 단위 환산으로서 경제적 가치가 같다고 말할 수 있습니다. 그러면 달러라는 공간과 원화라는 공간에서 각각의 벡터 합과 스칼라 곱을 정의할 수 있으며, 벡터공간의 공리를 만족함을 알 수 있습니다. 만일 달러에서 원으로 가는 함수를 $\phi$ 라고 쓴다면,

 

$$\phi (1 \;\mathrm{dollar})=1200 \;\mathrm{won}$$

$$ \phi (2 \;\mathrm{dollar})=2400 \;\mathrm{won}\\\\ \vdots$$

 

와 같이 어떤 한 달러의 원소에 대해 오로지 하나의 원화의 원소로 일대일 대응을 시킬 수 있는 것은 물론이고,

 

$$\phi(3 \;\mathrm{dollar}+4 \;\mathrm{dollar})=\phi(3 \;\mathrm{dollar})+\phi\left( 4 \;\mathrm{dollar} \right)$$

$$\phi(3 \;\mathrm{won}+4 \;\mathrm{won})=\phi(3 \;\mathrm{won})+\phi\left( 4 \;\mathrm{won} \right)$$

이런 식으로 선형임도 만족하게 됩니다.

 

이 짓거리를 수없이 반복하면, 그리고 만일 미국에 사는 미국인이라면 더욱이 달러 계산시 5달러+6달러는 그냥 5+6의 값을 구하는 수학 문제랑 똑같다는 사실을 알 수 있습니다. 금액이 오로지 양의 자연수 값만 가능하다고 가정하면, ^[각주:2] 달러 계산을 수행하는 달러 집합이나 자연수 집합은 별반 다를 것이 없어집니다.

 

그런데 연산을 생각해봅시다. 3달러와 4달러를 더하는 연산은 3+4에 사용된 기호 +와 엄연하게는 그 의미가 다릅니다. 달러와 달러를 더하는 행위는 달러 집합 안에서 정의된 합 연산이기 때문입니다. 근데 두 집합 또는 벡터공간이 동형이라면, 어차피 '그게 그거기' 때문에 이 연산마저 같은 것으로 취급해도 큰 문제가 발생하지 않게 됩니다.

 

 

이처럼 동형 관계에 놓여 있는 두 벡터공간은 그 집합의 실제적·물리적 형태가 완전이 같다는 것이 아니라 일대일 대응이 된다는 점에서 구조가 동일하다는 뜻입니다.

---

2. 선형변환과 행렬은 동형사상이다.

 

동형의 정의와 이와 관련된 정리를 한번 더 확인하고 갑시다. 이미 전전 시간에 학습한 내용입니다.

 

두 벡터공간 $V,W$ 에 대하여 선형변환 $T:V\rightarrow W$ 이 가역이면(=전단사이면), $V$와 $W$는 '동형(isomorphic)' 이라 하고 $V\cong W$ 라 표기한다. 이 때 가역인 선형변환을 $V$에서 $W$로 가는 '동형사상(isomorphism)'이라 한다.

정리($L.A$) 4.20
$V,W$가 같은 체에서 정의된 유한차원 벡터공간이라 하자. $V$가 $W$와 동형일 필요충분조건은 $\mathrm{dim}(V)=\mathrm{dim}(W)$ 인 것이다.

 

위 정리로부터 다음의 따름정리가 나옵니다.

 

따름정리($L.A$) 4.20.1

$F$-벡터공간 $V$에 대하여, $V$가 $F^n$과 동형이기 위한 필요충분조건은 $\mathrm{dim}(V)=n$ 인 것이다.

 

$F^n$의 정확한 뜻은 체 $F$에서 성분을 가져온 모든 $n$ 순서쌍($n-\mathrm{tuple}$)을 뜻합니다. $F^n$의 순서쌍도 괄호 안에 원소 $a_1,a_2,\cdots ,a_n$ 을 적어 쓰고 이를 행벡터 또는 열벡터로 나타냅니다. 

 

그런데 행벡터와 열벡터는 행렬로도 취급할 수 있지요? 즉 위 따름정리에 의하면 차원이 같은 경우 순서쌍과 행렬을 동형으로 만들 수 있음을 가리키는 것입니다. 순서쌍은 엄밀하게 시작하면 애초에 점의 좌표를 가리키는 것이 아니라, 그저 체의 원소들을 $n$개 나열한 것일 뿐인 것이고 벡터공간의 공리를 만족해서 벡터라 이름 불렸던 것입니다. 그런데 차원이 같은 경우 이를 벡터나 행렬로 다룰 수 있다는 결과를 얻어낸 것이고, 그 다음 3차원 직교 좌표계에서도 크기와 방향을 나타내는 위치벡터로서 의미를 가질 수 있었던 것입니다.

 

자, 그럼 이제 주제를 소개하겠습니다. 결과적으로, 선형변환과 행렬의 관계도 동형입니다.

$F$-벡터공간 $V,W$에 대하여 $V$에서 $W$로 가는 모든 선형변환의 모임으로 이루어진 벡터공간을 $\mathcal{L}(V,W)$ 라 표기한다. 만일 $V=W$ 이면 $\mathcal{L}(V,V)$ 는 간단히 $\mathcal{L}(V)$ 로 표기한다.

정리($L.A$) 4.23

차원이 각각 $n$과 $m$인 $F$-벡터공간 $V,W$를 생각하자. $V$와 $W$의 순서기저를 각각 $\beta,\gamma$ 라 할 때,
$T\in\mathcal{L}(V,W)$ 에 대하여 $\Phi_\beta^\gamma (T)=\left[ T \right]_\beta^\gamma$ 를 만족하는 함수

$$\Phi_\beta^\gamma:\mathcal{L}(V,W)\rightarrow M_{m,n}(F)$$
는 동형사상이다. 다시 말해 선형변환 집합과 행렬 집합은 동형사상이다.

 

$\Phi$ 는 선형변환 집합에서 행렬 집합으로 가는 함수입니다. 그런데 동형 관계는 벡터 공간 사이에서 하는 것이지 특정 선형변환 $T$와 그에 대응되는 행렬 사이에서만 하는 것이 아니기 때문에 집합과 집합 사이에서 정의된 것으로 $\Phi_\beta^\gamma:\mathcal{L}(V,W)\rightarrow M_{m,n}(F)$ 인 것입니다.

 

증명) 정리 ($L.A$) 4.10 에 의해 $\Phi_\beta^\gamma$는 선형이다. 추가로 $\Phi_\beta^\gamma$가 전단사임을 보여야 한다. 우선 정리 ($L.A$) 4.7 에 의하여 다음을 만족하는 선형변환 $T:V\rightarrow W$

$$T(v_j)=\sum_{i=1}^{m}A_{ij}w_i\;\;\;(1\leq j \leq n)$$
가 유일하게 존재한다. 이는 선형변환의 행렬표현의 정의에 따라 $\Phi_\beta^\gamma(T)=A$ 또는 $A=\left[ T \right]_\beta^\gamma$ 임을 의미하므로, $\Phi_\beta^\gamma$은 동형사상이다.

 

따름정리($L.A$) 4.23.1

유한차원 벡터공간 $V,W$의 차원이 각각 $n,\,m$ 일 때, $\mathcal{L}(V,W)$ 는 차원이 $nm$ 인 벡터공간이다.

---

3. 표준표현^[각주:3]

 

체 $F$에서의 $n$차원 벡터공간 $V$의 순서기저를 $\beta$라 하자. $\beta$에 대한 $V$의 '표준표현(Standard representation)'은,
$$x\in V \;\;:\;\; \phi_\beta (x)=\left[ x \right]_\beta$$
로 정의된 함수 $\phi_{\beta}:V\rightarrow F^n$ 이다.

 

표준표현이란 어떤 벡터 $x$를 $V$의 기저 $\beta$에 관한 좌표로 나타내는 방법을 말하는 것입니다. 좌표벡터를 정의한 방식과 매우 유사하죠? 쉽게 말해 표준순서기저를 택한 걸 기준, 표준으로 잡자 이 말입니다. 이 때 $V$는 $n$차원 벡터공간이니 기본적으로 $F^n$과 동형입니다.

 

우리는 이미 좌표사상이 동형임을 확인한 적이 있습니다. 다음 정리는 이의 재진술이며 증명하지 않겠습니다.

 

정리($L.A$) 4.24

임의의 유한차원 벡터공간 $V$와 이의 순서기저 $\beta$ 에 대하여 표준표현 $\phi_\beta$는 동형사상이다.

따름정리($L.A$) 4.24.1

$n$차원 벡터공간 $V$와 $F^n$는 동형이다.

 

따름정리가 어떻게 나올까요? $V$가 $n$차원 벡터공간일 때 $V$의 순서기저 $\beta$에 대해 표준표현을 할 시, 유일하고 오로지 단 하나의 값만이 나오므로, $V$와 $F^n$ 사이에 가역인 함수를 반드시 만들 수 있다는 겁니다. 따라서 $V$와 $F^n$은 동형이라는 것이죠.

 

이를 제대로 이해했다면 대부분의 교과서에 실려 있는 다음과 같은 사각형 그림을 이해할 수 있습니다.

 

 

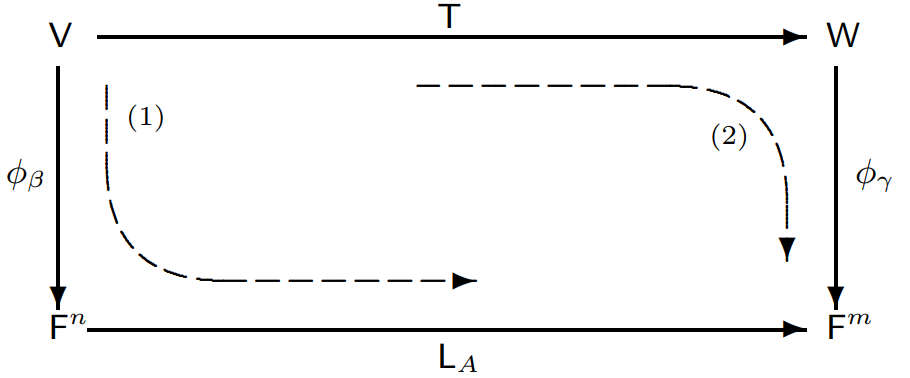
이 사각형은 윗변과 아랫변을 이항대립적으로 분석하시면 됩니다. $V,W$(=전자)와 $F^n,F^m$(=후자)의 차이가 뭘까요? 전자의 두 공간은 기저가 각각 $\beta,\gamma$ 인데 이건 문제에서 주어지는 대로, 임의의 벡터로 이루어진 기저가 될 수 있습니다. 반면 후자의 두 공간은 표준순서기저만을 택하라는 것입니다. 2차원 데카르트 좌표계면 $\mathbf{i},\mathbf{j}$를, 3차원 데카르트 좌표계면 $\mathbf{i},\mathbf{j},\mathbf{k}$를 택하라는 것이죠. 따라서 후자의 공간에서는 기저를 생까고 좌표만을 생각하면 됩니다! 마치 고등학교 수학에서처럼 말이죠. 그리고 이 방식이 $L_A$의 정수(精髓)임을 저번 글에서 역설했었죠?

 

대부분의 상황에서 기저는 간단(=크기가 1이고)하고 서로 수직일수록 좋습니다. 즉 '정규직교기저(Orthonormal basis)'^[각주:4]가 사실상 BEST인데, 연습 문제에서 그렇지 않은 기저를 줄 수도 있고, 내가 마주한 현실적 상황이 예쁜 기저를 가지지 않을 수도 있는데 그럴 땐 동형 관계를 이용해도 괜찮다는 겁니다. 그래서, 그림에 나온 대로 $V$에서 $F^m$에 도달하는 방식으로 $(1)$이나 $(2)$나 모두 괜찮다는 것입니다.

 

또한 $V$와 $F^n$은 동형이니, 표준표현(좌표함수) $\phi_\beta$를 이용해 둘을 동일시할수도 있겠죠. $W$와 $F^m$의 관계도 마찬가지입니다. 이 때는 $W$의 기저 $\gamma$와 연결지어야 하니 $\phi_\gamma$를 사용합니다. $T$와 $L_A$의 관계도 마찬가집니다. 둘 다 각각 윗변과 아랫변에서의 벡터공간을 연결해주는 선형변환으로 볼 수 있고 선형변환과 행렬은 동형이니 그들의 행렬표현도 존재하는 것입니다.

 

 

여담으로 한 마디만 하자면.. 아마 오늘 내용을 예습한 적 없이 처음 보는데 술술 읽어 내려가면서 완벽히 이해하시는 분은 거의 없을 거라고 생각합니다. 저 또한 선형대수학을 공부할 때 이 단원에서 처음으로 벽을 느껴 며칠동안 이해를 못했었습니다. 추후에 감을 잡고 몇 번 반복하다보니 글을 쓸 수 있는 수준에 도달았던 것이고요. 그러고 나서 검증된 수학 전공을 하신 아주 실력이 뛰어나신 분께 질문을 드렸던 적이 있습니다. 제가 그 때 '아니, 어차피 보통 정규직교기저만 쓰지 않나요?'라고 했지요. 그건 제가 물리학을 전공해서 그랬던 것 같습니다. 수학과이신 분은 '수학에선 아무(arbitrary) 기저나 써보고 싶어서 그런 것이다'라고 대답해 주셨던 같네요. 맞는 말입니다. 수학을 도구로 사용하는 분야에선 선형대수의 언어를 사용할 때 가장 최적화되어 있고 간편한 정규직교기저를 쓰는 것이 정상입니다. 다만 수학 그 자체를 연구하는 분야에서는, 임의의 기저를 연구하는 것이죠. 그래도 정규직교기저가 편한 것은 사실이니까, 임의의 기저와 정규직교기저 사이를 연결해주는 정당성을 확보하는 것이 바로 위 정리의 상징이라고 볼 수 있지 않을까 싶습니다.

 

 

[참고 문헌]

Linear Algebra : S.Friedberg, A.Insel, L.Spence, 5e, PEARSON

 

 

 

1. 이 '그림 이론'이라는 말 자체가 사실 그의 핵심 주장이기도 한 '말할 수 없는 것에 대해서는 침묵해야 한다'라는 명제와 정면 충돌하는 용어입니다. 실제로 비트겐슈타인이 '그림 이론'이라는 용어를 사용한 것이 아니고 이는 그의 철학을 연구한 후대 학자들이 붙인 말입니다.  [본문으로]
2. 예를 들어 지금 문제 상황을 간단히 하기 위해 -100원 같이 음의 금액이나, 루트 3달러 또는 1.5달러와 같은 값을 허용하지 않는다고 가정한다는 뜻입니다. [본문으로]
3. '표준'은 'standard'의 변역이며, '일반', '기준' 정도로 해석해도 큰 상관은 없습니다. [본문으로]
4. 이건 보통 선형대수학의 마지막 챕터로 배정되어 있는 내적공간이란 단원에 가서야 정식적으로 배우게 되는데, 그 개념은 이미 고등학교에서도 배우기 때문에 다들 알고 계실 겁니다. 벡터를 '정규화(normalization)'한다는 것은 어떤 벡터를 크기가 1인 벡터, 즉 단위벡터로 만드는 행위를 말합니다. 양자역학에서는 '규격화'라고 해서 파동함수의 전체적분값을 1로 만드는, 바로 그 계산입니다. 이는 벡터 크기를 제곱한 값의 역수를 앞에 달아주기만 하면 되지요. 나머지 '직교'라는 개념은 말그대로 수직한다는 겁니다. 즉 기저들끼리 수직한 관계가 갖추어졌을 때 가장 편한 형태가 된다는 겁니다. [본문으로]