이제 본격적으로 추상대수학에서 군론을 시작하려 합니다. 군론은 대수학에서도 매우 중요하지만, 환론과 체론이라는 여정을 떠나기 위해 반드시 알아야만 하는 선행개념입니다. 물리학에서는 대학원 수준의 양자역학에서 군론을 다루게 됩니다. 물리학에선 대칭성의 어마무시한 중요성을 피력하는 뇌터 정리 등 군을 통해 대칭성에 대한 풍부한 연구가 필요하기에, 고급 물리학을 공부한다면 양자역학에서 군론이 필요합니다. 이는 순수 대수학의 군론보다는 군론의 응용에 가깝기는 하나, 군의 기본 개념이 필요한 순간에도 봉착할테니 필수적으로 학습해야 합니다.
군, 환, 체에 대한 기초 개념은 이미 설명한 바가 있지만 선형대수학 정도의 수준에서 간단히 설명한 것이고, 본격적으로 군론을 추상대수학(현대대수학) 수준에서 시작하기 위해 정의를 해봅시다. 본질은 같습니다.
1. 군(Group)
1) 정의
Group 의 번역은 '군(群)' 으로, 한자를 보면 '무리 군'입니다. 상당히 괜찮은 번역이라 할 수 있습니다.
정의($A.A$) 2-6) 군(Group)
유닛으로만 이루어진 모노이드를 '군(group)'이라 한다. 다시 말해, 집합 $G$ 가 군이라는 것은 $G$ 가 다음의 $G1)\sim G4)$ 를 만족하는 것이다.
$G1)$ $G$ 는 주어진 이항연산에 대해 닫혀있다.
$G2)$ $G$ 의 원소들에 대해, 연산에 대한 결합법칙이 성립한다.
$G3)$ $G$ 의 원소들에 대해, $G$ 에는 주어진 이항연산에 대한 항등원이 존재한다.
$G4)$ $G$ 의 모든 원소들은 역원을 갖고 그 역원 역시 $G$ 에 포함된다.
따라서 어떤 집합이 군이면 어떤 하나의 연산 $*$ 가 주어지고 위 네 조건을 만족해야 한다. 이때 군을 $(G,*)$ 으로 표기한다. 연산의 혼동이 없는 경우 단순히 $G$ 라 표현한다.
추가로 $G5)$ 을 만족하는 군은, '아벨군(Abelian group 또는 Abelian)'이라고 한다.
$G5)$ $G$ 의 원소들에 대해, 연산에 대한 교환법칙이 성립한다.
집합이 군이 되기 위한 필요충분조건은 위에 적은 것처럼 닫힘성, 결합법칙, 항등원, 역원 이렇게 네 가지 특징을 가지고 있으면 됩니다. 또한, 반드시 하나의 연산이 주어져야 한다는 것을 명심해야 합니다. 대수학의 중~후반부에서 환을 다루게 되거나, 가군(module)의 개념 등을 다루게 될 때 연산의 개수가 1이 아닌 경우가 발생합니다.
아벨군에 대한 설명을 빼놓을 수 없습니다. 닐스 헨리크 아벨(Niels Henrik Abel) 은 대수학에 큰 기여를 한 수학자입니다. 아벨은 원래 맨 처음 어떤 좋은 대수적 성질을 갖는 집합을 군이라고 명명하려 했는데, 그 때 군이 되기 위한 조건에 '교환법칙'까지 추가했습니다. 위의 $G5)$ 까지 말이죠. 그렇다는 것은 교환법칙까지 성립하는 집합이 조금 더 수학적으로 깔끔하다, 연구할 성질이 많다, 이런 관점을 가졌다는 것을 뜻합니다. 하지만 이후 수학자들이 연구를 해 본 결과 교환법칙이 성립하지 않으면서 위 네 조건을 만족시키는 연산과 집합을 다루는 것이 더 일반적이라는 사실을 알아냈고, 그래서 현재 대수학에서는 군이 되기 위한 조건에서 교환법칙은 빼고, 대신 교환법칙이 성립하는 군에는 아벨의 이름을 붙여준 것이랍니다.
정의($A.A$) 2-6) 군의 위수1(Order of group)
$G$ 가 군일 때, $G$ 의 '위수(order)'란 $G$ 의 원소의 개수를 뜻하며 $\left| G \right|$ 로 표기한다.
이 군의 위수(오더) 개념은 순환군부터 끊임없이 몰아치는 녀석이니 미리 정의를 해두겠습니다. 사실상 그냥 집합의 원소 개수, 즉 기수 개념을 말하는 것입니다.
2) 대칭군
정의($A.A$) 1-4) 대칭군(Symmetric groups)
$X=\left \{ 1,2,\cdots,n \right \}$ 의 모든 치환들로 이루어진 집합 $S_n$은 함수의 합성 $\circ$ 를 연산으로 갖는 군이다. 덧붙여 $S_n$은 치환의 합성에 대한 항등원과 치환의 합성에 대한 역원이 존재하고, 이러한 군 $\left ( S_n,\circ \right )$ 을 '차수가 $n$인 대칭군(Symmetric group of degree $n$)'이라 부른다.
대칭군은 치환을 소개하면서 이미 설명을 끝내두었습니다. 정의를 다시 살펴보고, 이제 군론에서 대칭군을 어떻게 다루는지 예제 하나를 소개하려고 합니다.
예제1) 차수가 3인 대칭군 $S_3$ 을 모두 구하여라.
Sol) $S_3$ 는 간단해서 사용 빈도가 무지 높습니다. 자연스럽게 쓰다 보면 외워질 것입니다. 치환의 1행 표기법을 사용하여 원소를 나타내기도 하지만, 아래와 쓴 것처럼(순서를 지켜서) 기호 $\sigma$ 와 $\tau$ 를 사용하는 편입니다.
$$S_3=\left\{ (1) , (1 \; 2\; 3), (1\;3\;2) , (1\;2), (1\;3), \left( 2,3 \right) \right\} = \left\{
\varepsilon, \sigma, \sigma^2, \tau, \tau\sigma^2, \tau\sigma \right\}$$
이를 아래 사진처럼 표로 나타낼 수가 있습니다.
이렇게 어떤 군의 원소들끼리의 연산을, 모든 경우의수를, 마치 행렬과 같은 표로 나타낼 수 있는데, 이 표를 '케일리 표(Cayley table)'이라고 부릅니다.
3) 모노이드와 군의 특수한 관계
정리($A.A$) 2.7) 유닛으로만 구성된 모노이드는 군
만일 $M$이 유닛으로만 구성된 모노이드, 즉 $M$ 의 모든 원소가 역원을 갖고 그것이 $M$에 포함되면 $M$ 은 군이다. 이는 $M^*$ 으로 표기한다.
굳이 증명을 하지는 않겠습니다. 유심히 보아야 할 것은, $M^*$ 이라는 표기입니다. 유닛으로만 구성된 모노이드는 분명 군과 같은데 굳이 왜 정의나 정리를 쓰나? 라고 생각할 수 있지만, 유닛으로만 구성된 모노이드를 군이라 안부르고 굳이 '유닛으로만 구성된 모노이드'라고 부르는 이유는 원래 그 모노이드가 굳이 유닛으로만 구성될 필요는 없으나, 모노이드에서 유닛들만 남기고 다른 원소들을 제외하여 군을 만들 수 있는, 가능성이 있음을 어느 정도 시사하는 표현입니다. 즉 $M^*$ 이라는 표현은 관례적으로 $M$ 자체는 군이 아니지만 원소를 추려내서 군인 $M^*$ 으로 만들 수 있다, 이런 뜻을 내포한다고 볼 수 있습니다.
대표적인 것이 법 $n$ 에 대한 정수집합 $\mathbb{Z}_n$ 입니다.2 연산이 곱셈인 경우에 이 집합을 고려하면 항상 역원이 존재하지 않습니다. 그런데 역원이 존재하기 위해서는 (정수론에서 배운) 결국 $\bar{a}\bar{b}=1$ 인 원소 $\bar{b}$ 가 존재한다는 것이니,
$$\mathbb{Z}_n^*=\left\{ a\in \mathbb{Z}\mid \gcd(a,n)=1 \right\}$$
가 됩니다. 이렇게, $\mathbb{Z}_n$ 자체는 원래 군이 아닌 모노이드지만 적당히 원소를 추려내어 군이 될 수 있음을 보여주기 위해 이 정리 및 표기법이 쓸모없는 것은 아니라는 뜻입니다.
4) 직곱
군론에서 종종 등장하는 개념 하나를 소개합니다. 그리 어렵지는 않은데, 매우 중요합니다.
정의($A.A$) 2-7) 직곱(Direct product)
집합 $G_1,G_2,\cdots ,G_n$ 에 대해 카르테시안 곱(cartesian product) $G_1\times G_2\times \cdots \times G_n$ 은 $g_i\in G_i$ 들로 이루어진 모든 순서쌍 $(g_1,g_2,\cdots g_n)$ 들의 집합을 가리킨다. 만일 $G_i$ 들이 모두 군이면, 이 순서쌍들의 집합 역시 군이된다.
만일 $G_1,\cdots , G_n$ 이 모두 군이면, 집합 $G_1\times \cdots \times G_n$ 을 이들의 '직곱(direct product)'라 하고,
$$\left( g_1,g_2,\cdots ,g_n \right)\circ \left( g'_1,g'_2,\cdots ,g'_n \right)=\left( g_1g'_1,g_2g'_2,\cdots ,g_n g'_n\right)$$ 와 같이 정의한다. 여기서 $g_ig'_i$ 는 $G_i$ 에서의 각각의 $i$ 에 대한 곱이다.
정리($A.A$) 2.8)
$G_1,\cdots ,G_n$ 모두 군이라고 하자. 그러면 이들의 카르테시안 곱 $G_1\times G_2\times \cdots \times G_n$ 역시 군이고, 항등원은 $(1,1,\cdots , 1)$ 이며 역원은 $\left( g_1,g_2,\cdots ,g_n \right)^{-1}=\left( g_1^{-1},g_2^{-1},\cdots ,g_n^{-1} \right)$ 이다.
5) 군에서 성립하는 여러 법칙
군도 모노이드라서, 모노이드의 법칙들을 그대로 가져와 쓸 수가 있습니다.
정리($A.A$) 2.9)
$g,h,g_1,g_2,\cdots g_{n-1}, g_n$ 가 군 $G$ 의 원소들이라고 하자.
① $1^{-1}=1$
② $(g^{-1})^{-1}=g$
③ $(gh)^{-1}=h^{-1}g^{-1}$ 이다.
④ $\left( g_1g_2\cdots g_n \right)^{-1}=g_n^{-1}\cdots g_2^{-1}g_1^{-1}$
⑤ 0보다 크거나 같은 정수 $n$에 대하여 $(g^n)^{-1}=g^{-n}$ 이다.
정리($A.A$) 2.10) 군에서 지수법칙이 성립한다.
군 $G$ 의 두 원소 $g,h\in G$ 에 대하여 다음이 성립한다.
① 정수 $n,m$ 에 대하여, $g^ng^m= g^n+m$
② 정수 $n,m$ 에 대하여, $\left( h^n \right)^m=h^{nm}$
③ $gh=hg$ 이면 정수 $n$ 에 대하여, $\left( hg \right)^n=g^nh^n$
모노이드에서 성립했던 것을 자연스레 끌고 왔으니, 모노이드에서 위 법칙을 증명했다면 굳이 또 증명할 필요는 없겠지요. 모노이드 글에서 빠짐없이 전부 다 증명했던 것이니 증명을 하고 싶다면 해당 글을 참고하시면 됩니다.
이 다음부터는 일반 모노이드에서가 아닌, 군에서만 성립하는 것들입니다.
정리($A.A$) 2.11) 소거법칙(Cancellation laws)
군 $G$ 의 세 원소 $g,h,f\in G$ 에 대하여 다음이 성립한다.
① 좌측 소거(Left cancellation) : 만일 $gh=gf$ 이면, $h=f$ 이다.
② 우측 소거(Right cancellation) : 만일 $hg=fg$ 이면, $h=f$ 이다.
증명) ① $gh=gh$ 이면, $g\in G$ 이므로 $g^{-1}$ 가 존재하여 양변의 왼쪽에 이를 곱한다. 그러면 $1h=f$ 이다.
② 동일한 논리로 $hg=fg$ 의 양변 우측에 $g^{-1}$ 를 곱하여 얻는다. $_\blacksquare$
우리가 흔히 양변에 역원을 곱해 '지운다'라는 표현을 드디어 군이라는 집합에서부터 가능해진다는 것입니다. (모노이드에서는 반드시 그렇지 않은 셈입니다!) 엄밀히 따지면 $g$ 에 $g^{-1}$ 을 곱하면 $gg^{-1}=1$ 으로 항등원이 탄생한다는 논리입니다.
정리($A.A$) 2.12)
군 $G$ 의 원소 $g,h\in G$ 에 대하여 다음이 성립한다.
① 방정식 $gx=h$ 는 유일한 해 $x=g^{-1}h\in G$ 를 갖는다.
② 방정식 $xg=h$ 는 유일한 해 $x=hg^{-1}\in G$ 를 갖는다.
증명) 소거법칙을 이용하면 해를 갖는 것은 쉽게 보일 수 있다. 유일성의 증명하자. ①에서, $gx=h$ 외에 또 다른 해 $y$ 가 존재하여 $gy=h$ 라고 하자. 그러면 $h=gx=gy$, 곧 $gx=gy$ 이고 좌측에서 $g$ 의 역원을 곱해 $g$ 를 소거하면 $x=y$ 이다. 이는 $x\neq y$ 라는 가정에 모순이다. 따라서 이 방정식은 유일해를 갖는다. ②에 대해서도 비슷하게 증명하면 된다. $_\blacksquare$
따름정리($A.A$) 2.12.1)
군 $G$ 에 대한 케일리 표(Cayley table)의 모든 행과 열에는 $G$ 의 각 원소가 반드시 한 번만 나타난다.
증명) 아래 [그림 2]를 같이 참조하자. 서로 다른 세 원소 $a,x,y$ 가 군 $G$ 의 원소 라고 하자. 그러면 $x,y$ 는 각각 서로 다른 자리에 적는다. $a$ 와 곱해져 $ax, ay$ 가 존재하는 행에서 $ax, ay$ 는 서로 다른 자리에 놓인다.
이제 정리$(A.A)$ 2.11, 2.12 에 의하여, 만일 $ax=ay$ 이면 좌측 소거법에 의하여 $x=y$ 이다. 이것의 대우 명제로부터, $x\neq y$ 이면 $ax\neq ay$ 이 성립한다. 즉, 만일 $x,y$ 가 서로 다른 $G$ 의 원소이면 $ax\neq ay$ 이므로 한 행 또는 한 열에 같은 원소가 두 번 등장할 수 없다. $_\blacksquare$
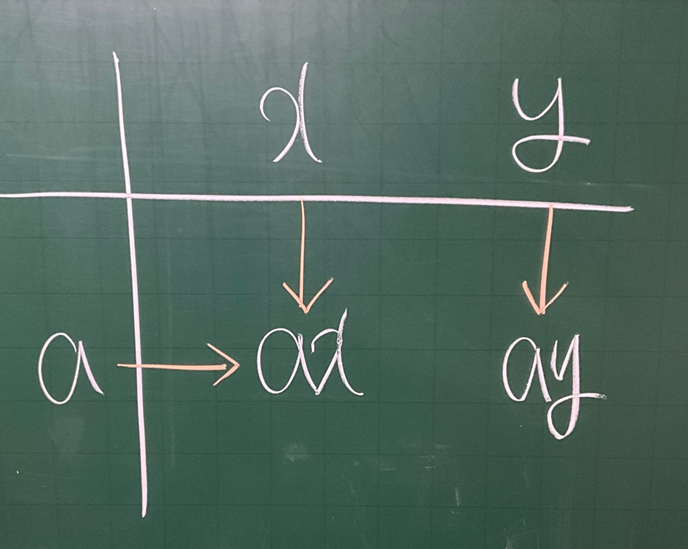
위 증명을 조금 풀어 써볼까요? 만일 $x\neq y$ 일 때, $ax=ay$ 인 상황이 발생하면, 케일리 표에서 한 행(또는 한 열)에 같은 원소가 두 번 등장함을 뜻합니다. 위 그림에서 $ax=ay$ 이니까요. 하지만 우리는 정리 $(A.A)$ 2.11, 12 로부터 만일 $x\neq y$ 이면 $ax\neq ay$ 라는 것을 유도할 수가 있습니다. 그렇기 때문에 절대로 $ax=ay$ 즉 케일리 표에서 동일 원소가 한 행 또는 열에 두 번 이상 등장 불가능하다는 것입니다. (케일리 표를 적을 때, 0행과 0열에는 각각 서로 다른 $G$ 의 원소를 적으므로 이 표에서 애초에 $x=y$ 일 수는 없습니다. 만일 그렇게 그렸다면 애초에 케일리 표 자체를 잘못 적은 셈입니다.)
여기까지 하면 일반적인 군에 대한 기초 중의 기초는 맛본 셈입니다. 이를 바탕으로 꾸준히 쭉쭉 여러 개념을 소개해 보겠습니다.
[참고문헌]
Introduction to Abstract Algebra, 4e, W.Keith Nicholson
'대수학(Abstract Algebra) > 군론' 카테고리의 다른 글
| 부분군(Subgroup) (0) | 2024.02.23 |
|---|---|
| 대수학에서 모노이드(Monoid in Algebra) (0) | 2024.02.23 |
| 이항연산과 마그마(Binary operations and Magma) (1) | 2023.04.15 |
댓글