군에 여러 종류가 있지만 제가 생각하기에 가장 많이 등장하면서 중요도가 높아 으뜸으로 칠 수 있는 것 바로 순환군입니다. 순환군은 말그대로 무언가가 계속 돌아가면서 반복된다는 뉘앙스를 가지고 있는데 실제 그 특성이 순환군에서 잘 드러나게 됩니다.
그러나 주의점이 있습니다. 순환군은 정수론의 기본 개념들을 알지 못하면 제대로 분석하는 것이 불가능에 가깝습니다. 구체적으로는 정수론에서 합동의 의미, 선형합동식을 푸는 방법, 정수론에서 잉여류(동치류)의 개념, 그들의 연산법을 전부 알아야 합니다. 정수론을 잘 모르더라도 이러한 개념은 각잡고 1주일 정도만 공부하면 해결하는 것이 어렵지 않습니다.1 반드시 이 모든 글에 적혀있는 개념을 정독하고 오시는 것을 권합니다. 이제 순환군을 한 번 살펴보겠습니다.

https://blog.naver.com/cindyvelyn/223259697062
1. 순환군
1) 정의
정의($A.A$) 2-12) 순환군과 생성원
$G$ 가 군일 때 특정 원소 $g\in G$ 의 거듭제곱들로만 구성된 원소를 '순환군(Cyclic group)'이라고 한다. 자연수 $n\geq 1$ 이 주어졌을 때, 위수가 $n$ 인 순환군(cyclic group of order $n$)은2
$$\left\langle a \right\rangle=C_n=\left\{ 1,a,a^2,\cdots ,a^{n-1} \right\}$$ 으로 나타내며 여기서 $a^n=1$ 이다. 이때, $a$ 를 순환군 $C_n$ 의 '생성원(generator)'이라고 한다.
정의($A.A$) 2-13) 순환 부분군
$G$ 가 군일 때, $g\in G$ 에 대해 $\left\langle g \right\rangle=\left\{ g^k\mid k\in\mathbb{Z} \right\}$ 는 '$g$ 에 의해 생성된 $G$ 의 순환 부분군(cyclic subgroup of $G$ generated by $g$)'라고 한다.
순환군은 말그대로 하나의 원소를 계속 거듭제곱할 때 그들을 전부 원소로 갖는 집합에 해당합니다. 그리고 거듭제곱을 하는 가장 기본이 되는 대상을 생성원이라고 부릅니다.
또한 $g\in G$ 를 아무거나 택했을 때, 그것의 거듭제곱으로 만들어 낸 집합 $\left\langle g \right\rangle$ 은 부분군이 됩니다. 실제로 부분군이 되는지 확인이 필요하고, 이것의 주요한 특징에 대해 서술한 것이 아래의 정리입니다.
정리($A.A$) 2.17)
군 $G$ 에 대해 $g\in G$ 를 생각하자.
① $\left\langle g \right\rangle=\{ g^k\mid k\in\mathbb{Z} \} \leqslant G$ 이다.
② $g\in H$ 인 모든 $H\leqslant G$ 에 대해, $\left\langle g \right\rangle\subseteq H$ 이다. 즉 $\left\langle g \right\rangle$ 는 $g$ 를 포함하는 가장 작은 $G$ 의 부분군이다.
증명) ① i) $g^0=1\in \left\langle g \right\rangle$ 로 항등원이 존재한다.
ii) $x,y\in \left\langle g \right\rangle$ 라 하자. $xy\in \left\langle g \right\rangle$ 가 만족되어야 한다. 그러면 $g^k=x$ 이고 $g^m=y$ 를 만족하는 $k,m\in\mathbb{Z}$ 가 존재한다. $k+m\in\mathbb{Z}$ 이므로 지수법칙에 의하여 $xy=g^{k+m}\in \left\langle g \right\rangle$ 이 성립한다.
iii) $x\in \left\langle g \right\rangle$ 라 하자. 그러면 $x=g^k$ 가 되는 $k\in\mathbb{Z}$ 가 존재한다. $g\in G$ 이므로, $g^{-1}$ 또한 존재하며, $-k\in\mathbb{Z}$ 이므로 $(g^{-1})^k=g^{-k}=x^{-1}\in \left\langle g \right\rangle$ 이 성립한다.
② $g\in H\leqslant G$ 라 하자. $H$ 가 군이므로 닫혀있기 때문에, $g\cdot g=g^2\in H$ 이어야 한다. 그러면 또 닫힘성에 의해 $g^2\cdot g^2=g^4\in H$ 이고 $g\cdot g^2=g^3\in H$ 역시 성립한다. 따라서 임의의 $k\in\mathbb{Z}$ 에 대해 $g^k\in H$ 가 성립한다. 이는 $g$ 를 포함하는 $G$ 의 모든 부분군은 반드시 필수적으로 $g$ 의 거듭제곱들을 포함해야 한다는 것으로, $\left\langle g \right\rangle$ 가 가장 작은 $g\in G$ 를 포함하는 $G$ 의 부분군임을 뜻한다. $_\blacksquare$
아래 예제는 순환군의 개념을 이해하기 위해 반드시 짚고 넘어가야 하는 것들을 제가 간추린 것입니다. 매우 매우 중요하고 뒤쪽의 대수 개념들을 다룰 때 반드시 필요하기 때문에 꼭 꼼꼼히 이해하고 넘어가는 것을 추천합니다.
예제 1) 군 $G=\{ 1, -1, i, -i \}$ 를 생각하자. 이것이 순환군임을 확인하고 생성원을 찾아라.
Sol) 생성원은 $i$ 와 $-i$ 로 두 개이다.3 이들을 계속 거듭제곱하면 나머지 셋 원소를 다 만들 수 있기 때문이다. $i^2=-1, i^-3=-i, i^4=1$ 이라는 사실로부터 알 수 있다. 하지만 $1,-1$ 은 생성원이 되지 못한다. 이들을 반복하여 곱해도 $i,-i$ 를 만들 수 없기 때문이다. 따라서 $G=\left\langle i \right\rangle=\left\langle -i \right\rangle$ 이다. $_\blacksquare$
예제 2) [군의 연산이 덧셈인 경우] 군 $(X,+)$ 을 생각하자. $x\in X$ 에 의해 생성되는 순환 부분군은
$$\left\langle x \right\rangle=\{ kx\mid k\in\mathbb{Z}\} := x\mathbb{Z}$$
와 같이 나타날 수 있고 $x$ 의 배수들로 이루어진 집합이다. 그러면 여기서 $x^n=nx$ 의 의미를 가지고, 항등원은 $0$ 이며, $x\in X$ 의 역원은 $x^{-1}$ 로 표기할 수 있다. 군에서는 지수법칙이 성립하고 여기서의 연산을 바탕으로 하면
$$x^{n+m}=x^nx^m\;\;\Longleftrightarrow \;\;(n+m)x=nx+mx $$
$$(x^n)^m=x^{nm}\;\;\Longleftrightarrow \;\; m(nx)=(mn)x $$
$$(xy)^n=x^nx^m\;\;\Longleftrightarrow \;\; n(x+y)=nx+ny$$
가 된다. 그러면 예컨대 $x=3$ 을 택하자. 그러면 $\left\langle 3 \right\rangle=\left\{ \cdots , -6, -3, 0, 3, 6,\cdots \right\}$ 으로 나타낼 수 있다. 여기서 $3^{-1}$ 의 의미는 수학적으로 역의 지수를 뜻하는 의미가 아니니 $3^{-1}\neq \displaystyle\frac{1}{3}$ 이고, $3^{-1}=-3$ 으로 $3$ 의 덧셈에 대한 역원이라고 이해해야 적절하다. 그러면 $3^{-4}$ 의 의미는 무엇인가?
Sol) 지수가 음수이면 지수법칙을 써서 역원의 거듭제곱으로 바꿔 이해해야 한다. 즉,
$$3^{-4}=(3^{-1})^4=\underset{\text{Add}\;3^{-1}\;\text{four times}}{(3^{-1}+3^{-1}+3^{-1}+3^{-1})}=-3\cdot 4=-12$$
의 의미를 갖는다. 결과적으로 보면, 덧셈의 연산이 주어진 이 군에서는 $3^{-4}=-(3\cdot 4)$ 로 처리해도 좋다. 즉 지수법칙을 쓸 때 음의 지수가 포함되어 있는 경우($k\geq 0,\ k\in\mathbb{Z}$)
$$x^{-k}=-k\cdot x$$
와 같이 생각해도 좋다. $_\blacksquare$
예제 3) $(\mathbb{Z},+)$ 은 생성원이 $1$ 과 $-1$ 로 유일한 순환군이다. 이에 대해 논하여라.
Sol) 임의의 $k\in\mathbb{Z}$ 에 대해
$$k=k\cdot1=\underset{\text{Add}\;1,\;k\;\text{times}}{(1+1+\cdots + 1)}\in \left\langle 1 \right\rangle
=\left\{ k\cdot1\mid k\in\mathbb{Z} \right\}$$
가 성립한다. 즉 임의의 정수는 $\left\langle 1 \right\rangle$ 에 포함된다. 여기서 $k\geq 0$ 인 정수에 대해서는 위의 해석이 직관적으로 납득되지만 $k=-5$ 와 같이 음수라면 $-5$번 더한다는 행위를 어떻게 이해할 수 있을까? 위의 예제 2)에서 했던 것과 같이 역원을 $5$ 번 더한다고 이해해야 한다. 즉
$$1^{-5}=(1^{-1})^5=\underset{\text{Add}\;-1,\;5\;\text{times}}{\left\{ (-1)+(-1)+(-1)+(-1)+(-1) \right\}}=(-1)\cdot 5=-5$$
으로 납득할 수 있다.4
비슷하게 만일 $-1$ 을 생성원으로 택한다면 임의의 음의 정수 $k$ 는 $-1$ 을 $-k>0$ 번 더한다고 다음과 같이 해석한다.
$$0> k:=(-1)^k=-k\cdot(-1)=\underset{\text{Add}\;-1,\;-k\;\text{times}}{\left\{ (-1)+(-1)+\cdots+(-1) \right\}}
\in \left\langle -1 \right\rangle
=\left\{ k\cdot1\mid k\in\mathbb{Z} \right\}$$
반면 양의 정수를 $-1$ 로 만들어 낼 때는, $p=7$ 로 예를 들어서 생각해보자. 이때는 $-1$ 의 역원 $1$ 을 $p=7$ 번 더한다고 해석해야 한다.
$$7:=(-1)^{-7}=((-1)^{-1})^7=\underset{\text{Add}\;1,\;7\;\text{times}}{\left\{ 1+\cdots+1 \right\}}=1\cdot 7=7$$
만일 $1,-1$ 이 아닌 다른 정수를 택하면 정수 집합 전체의 임의의 원소를 생성하지 못하므로, 덧셈이 주어진 정수집합군 $(\mathbb{Z},+)$ 의 생성원은 $1,-1$ 이 유일하다. $_\blacksquare$
예제 4) 정수론에서 잉여류와 법 $n$ 에 대한 정수집합을 다룬 바가 있다. $(\mathbb{Z}_n, +)$ 는, 생성원이 $\overline{1}$ 인 순환군임을 보여라.
정의($N.T$) 3-4) 정수론에서 잉여류(residue class)
정수 $a$ 의 '법 $n$ 에 대한 잉여류(residue class modulo $n$)' 란 다음과 같이 정의하고 표기한다.
$$\overline{a}:=\left[ a \right]=\left\{ x\in\mathbb{Z}\mid x\equiv a \;(\text{mod}\; n) \right\}$$ 풀어서 설명하자면, $\overline{a}$ 는 법 $n$ 에 대해 정수 $a$ 와 합동인 모든 정수들을 모든 동치류(집합)를 말한다.5
잉여류에서 문자가 헷갈려요 $\Longrightarrow$ 법 $n$ 은 '나누는 수'이고, 동치류(잉여류) $a$ 는 '나머지'다.
정의($N.T$) 3-5) 잉여류들로 구성된 집합
법 $n\in\mathbb{N}$ 이 주어졌을 때, 다음의 집합을 '법 $n$ 에 대한 정수 집합(Sets of integers modulo $n$)'이라고 정의한다. 이는 곧 법 $n$ 에 대한 모든 서로 다른 $n$ 개의 잉여류들을 원소로 갖는 집합을 말한다.
$$\begin{align*}
\mathbb{Z}_n&:=\left\{ \overline{a}\mid \overline{a}=
\left\{ x\in\mathbb{Z}\mid x\equiv a \;(\text{mod}\; n) \right\}\;,\;a\in\left\{ 0,1,2,\cdots n-1 \right\}
\right\}
\\\\&=\left\{\overline{0},\overline{1},\overline{2},\cdots \overline{n-1} \right\}
\end{align*}$$
Sol) 자연수 $n$ 이 주어졌을 때 $\overline{1}=\left\{ x\in\mathbb{Z}\mid x\equiv 1\;(\text{mod}\; n) \right\}$ 을 뜻한다. 즉 $\overline{1}$ 은 $n$ 으로 나누었을 때 나머지가 $1$ 인 정수들을 말한다. 이때 $1\leq k \leq n-1$ 인 $k\in\mathbb{N}$ 에 대하여 $\overline{1}+\overline{k}=\overline{k+1}$ 이 성립하므로, $\overline{k}=k\overline{1}$ 이 성립한다. 따라서 $\overline{k}\in \left\langle 1 \right\rangle$ 이므로, $\mathbb{Z}_n=\left\langle \overline{1} \right\rangle$ 이다. $_\blacksquare$
예제 5) [정수론에서 확장] $\mathbb{Z}_n$ 으로 주어지는 경우 연산은 덧셈이며, 고로 $(\mathbb{Z}_n,+)$ 의 구조이다. 반면 $\mathbb{Z}_n^*$ 이라는 집합은 다음과 같이 정의된다. 정수론에서 합동, 선형합동식을 이야기한 뒤에 소개한 적이 있었다.
정의($N.T$) 3-7)
법 $n\in\mathbb{N}$ 이 주어졌을 때, 다음의 집합을 '법 $n$ 에 대한 곱셈 정수 집합(Sets of multiplicative integers modulo $n$)' 이라고 정의한다. 이는 곧 $\mathbb{Z}_n$ 의 원소 중 곱셈 연산에 대해 역원을 가지는 원소들만을 추려 뽑아 만든 집합으로, $\overline{a}x\equiv 1 \;(\text{mod}\; n)$ 을 만족하는 동치류 $\overline{a}$ 들로 구성된 집합이다. 이를 조건제시법으로 나타내면 다음과 같다.
$$\mathbb{Z}_n^*:=\left\{ \overline{a}\in\mathbb{Z}_n\mid \gcd(a,n)=1
\right\}\subseteq \mathbb{Z}_n$$
따름정리($N.T$) 3.12.1)
$\overline{a}x\equiv 1\;(\text{mod}\;n)$ 이 성립할 필요충분조건은 $\gcd(a,n)=1$ 인 것이다.
여기서는 연산이 곱셈이며, 따라서 $(\mathbb{Z}_n^*, *)$ 의 구조이다. 이때 $\mathbb{Z}_7^*$ 의 원소를 동치류의 원소나열법으로 표현하여라.
Sol) $\gcd(a,7)=1$ 이 되는 $a$ 의 값을 모두 검토한다. $0\leq a \leq 6\;,\;a\in\mathbb{Z}$ 인 것이므로, $a=0,1,2,\cdots ,6$ 에 해당한다. $a=0$ 을 제외하면 이들은 모두 $\gcd(a,7)=1$ 을 만족한다. 따라서 $\mathbb{Z}_7^*:=\left\{ \overline{1},\overline{2},\overline{3},\overline{4},\overline{5},\overline{6}
\right\}\subseteq \mathbb{Z}_7$ 으로 표현할 수 있다. $_\blacksquare$
2. 위수
1) 정의
군의 위수에 대해서는 이미 군에 대한 글에서 다룬 바 있습니다.
정의($A.A$) 2-14) 군의 위수(Order of group)
$G$ 가 군일 때, $G$ 의 '위수(order)'란 $G$ 의 원소의 개수를 뜻하며 $\left| G \right|$ 로 표기한다.
원소에 대해서도 위수 개념을 정의할 수 있습니다. 군의 위소나 원소의 위수는 일단 비슷해 보이기는 하지만 정의는 다르며, 둘의 밀접한 관계는 사실 $\left| g \right|=\left| \left\langle g \right\rangle \right|$ 의 관계가 성립하며 아래에서 나중에 다루게 됩니다.
정의($A.A$) 2-15) 원소의 위수(Order of element)
군 $G$ 에 대해 원소 $g\in G$ 를 고려하자. 다음 조건을 만족시키는 자연수 $n$ 을 원소 $g$ 의 '위수'라 하고 $\left| g \right|=n$ 이라 표기한다.
① 유한위수(finite order) : 어떤 정수 $k\neq 0$ 에 대해 $g^k=1$ 이면, $g^n=1$ 을 만족하는 가장 작은 자연수 $n\geq 1$ 을 $\left| g \right|=n$ 로 정의한다.
② 무한위수(infinite order) : $g^k=1$ 이 오직 $k=0$ 일 때만 성립하는 경우, $\left| g \right|=\infty$ 라 정의한다.
정리($A.A$) 2.18)
$G$ 가 유한군이라고 하자. 그러면 모든 $g\in G$ 의 위수도 유한하다.
증명) $G$ 가 유한군이면 임의의 $g\in G$ 에 대하여 $g,g^2,g^3,\cdots $ 들이 전부 서로 다를 수는 없다. 즉 $g^k=g^m$ 이 되는 $k,m\in\mathbb{Z}$ 가 존재해야 하고 이때 일반성을 잃지않고 $k<m$ 이라고 하자. 그러면 $g^{m-k}=1$ 이며 $0< m-k\in\mathbb{Z}$ 이므로 $g$ 의 위수6도 유한하다.
그러니까 원소의 위수 개념은 그 원소를 거듭제곱해서 항등원 $1$ 이 될 수 있을 때, 그 $1$ 이 되게 하는 거듭제곱 지수 중 가장 작은 값을 말합니다. 예를 들어서 어떤 $g\in G$ 에 대해 $g\neq 1$ 이고 $g^2\neq 2$ 라고 합시다. 이때 $g^3=g^6=g^9=\cdots =1$ 이 성립한다고 하면, 이 지수값 중 가장 작은 $3$ 이 $g$ 의 위수가 됩니다.
예제 6) $\mathbb{Z}_8^*= \{ \overline{1},\overline{3},\overline{5},\overline{7} \}$ 이다. 이것은 순환군인가? 각 원소들의 위수를 검토해봄으로서 판단해 보아라.
Sol) 우선 $\mathbb{Z}_8^*$ 의 정의 상 연산은 자동으로 곱임을 알 수 있다. 원소들 하나씩에 대해 위수를 먼저 구해보자.
i) $\overline{1}^1=\overline{1}$ 이므로, $\left| \overline{1}\right|=1$ 이다.
ii) $\overline{3}^2=\overline{9}=\overline{1}$ 이다. 여기서 두번째 등호가 성립하는 까닭은 $9\equiv 1 \;(\text{mod}\; 8)$ 이기 때문인 사실에 주목하자. 따라서 $\left| \overline{3} \right|=2$ 가 된다.
iii) $\overline{5}^2=\overline{25}=\overline{1}$ 이다. 두번째 등호가 성립하는 까닭은 위에서와 같다. 고로 $\left| \overline{5}\right|=2$ 이다.
iv) 똑같은 논리로 $\overline{7}^2=\overline{49}=\overline{1}$ 이다. 그러면 $\left| \overline{7}\right|=2$ 이다.
모든 원소들을 살펴보았을 때 원소들의 위수가 $1$ 또는 $2$ 이다. $\left| \mathbb{Z}_8^*\right|=4$ 이므로 위수가 $3$ 인 원소가 있어야 이것이 순환군이 될 수 있다. 하지만 그렇지 않으므로 $\mathbb{Z}_8^*$ 은 순환군이 아니다. $_\blacksquare$
정리($A.A$) 2.19) 자신과 역원의 위수는 같다
$G$ 가 군이고 임의의 $g\in G$ 를 생각하자. 그러면 $\left| g \right|=\left| g^{-1} \right|$ 이다.
증명) $k\in\mathbb{Z}$ 에 대하여 $(g^{-1})^k=(g^k)^{-1}$ 이다. 그러면 $g^k=1 \;\;\Longleftrightarrow \;\; (g^{-1})^k$ 이며, 따라서 이것이 성립하게 하는 $k$ 의 최솟값 $n$ 은 $g$ 의 위수이고 이 값은 $g^{-1}$ 의 위수와도 같을 수밖에 없다. $_\blacksquare$
2) 원소의 위수의 성질
아래 성질은 순환군과 밀접하긴 하지만 꼭 순환군에 대해서만 성립하는 것은 아닙니다. 아주 애용하는 성질이니 반드시 암기가 필요할 정도로 숙달해야 합니다. 위수가 유한한 경우와 무한한 경우 두 가지 version 으로 나누어 살펴보겠습니다.
정리($A.A$) 2.20)
$G$ 가 군이고 $g\in G$ 이며 $\left| g \right|=n\in\mathbb{N}$ 이라고 하자. 그러면 다음이 성립한다.
① $g^k=1 \;\; \Longleftrightarrow \;\; n\mid k$
② $g^k=g^m \;\; \Longleftrightarrow \;\; k\equiv m \;(\text{mod}\; n)$
③ 순환군 $\left\langle g \right\rangle=\left\{ 1,g,g^2,\cdots ,g^{n-1} \right\}$ 에 대하여 $1,g,g^2,\cdots , g^{n-1}$ 들은 서로 다른(distinct) 값이다.
증명) ① $\Longleftarrow$ : $n\mid k$ 이면 $q\in\mathbb{Z}$ 에 대하여 $k=qn$ 으로 쓸 수 있다. 그러면 $g^k=(g^n)^q=1^q=1$ 이 성립한다.
$\Longrightarrow$ : $g^k=1$ 이라고 가정하자. 나눗셈 알고리즘을 사용하면 $k=qn+r$ 이 되게 하는 $q,r\in\mathbb{Z}$ 이 존재하고 이때 $0\leq r <n$ 이 성립하게 된다. 그러면
$$1=g^k=g^{qn+r}=(g^n)^q\cdot g^r=g^r$$
의 관계가 성립한다. 그러면 가능한 경우의 수는 $r$ 이 $n$ 의 배수가 되거나 $0$ 이어야 한다는 것이다. 그러나 나눗셈 알고리즘을 사용하였으니 $r$ 값의 범위에 따라 $r < n$ 이어야만 하므로 $r\neq n$ 이고 $r=0$ 임을 알 수 있다. 이는 $k=nq$ 라는 것이므로, $n\mid k$ 이다.
② $g^k=g^m$ 인 것은 $g^{k-m}=1$ 인 것과 필요충분조건이다. 이는 다시 $n\mid (k-m)$ 과 필요충분조건이고, 따라서 합동의 정의에 의하여 $k\equiv m\;(\text{mod}\; n)$ 이다.
③ $\left\langle g \right\rangle$ 에 존재하는 어떤 두 원소가 같다고 가정하여, $g^k=g^m$ 이라고 해보자. 이때 범위는 $0\leq k \leq m < n$ 이라고 가정한다. 그러면 $g^{m-k}=1$ 이며 이때 $0\leq m-k <n$ 이다. 그런데 원소의 위수의 정의에 의하면 $n$ 은 $g$ 의 거듭제곱식이 항등원이 되게하는 최소의 값이다. 따라서 $0\leq m-k <n$ 의 범위와 $n$ 의 최소성을 고려하면 $m-k=0$ 이 되어야 하고, 고로 $g^k=g^m$ 임을 얻는다. 따라서 $1,g,g^2,\cdots ,g^{n-1} $ 은 서로 다른 값이다. $_\blacksquare$
정리($A.A$) 2.21)
$G$ 가 군이고 $g\in G$ 이며 $\left| g \right|=\infty$ 라고 하자. 그러면 다음이 성립한다.
① $g^k=1 \;\; \Longleftrightarrow \;\; k=0$
② $g^k=g^m \;\; \Longleftrightarrow k=m$
③ 순환군 $\left\langle g \right\rangle=\left\{ \cdots, g^{-2}, g^{-1}, 1,g,g^2,\cdots \right\}$ 에 대하여 $\cdots, g^{-2}, g^{-1}, 1,g,g^2,\cdots $ 들은 서로 다른(distinct) 값이다.
따름정리($A.A$) 2.21.1)
군 $G$ 에 대하여 임의의 $g\in G$ 를 생각하자. 그러면 이 원소를 생성원으로 하여 만든 순환군의 위수와 이 원소의 위수는 같다. 즉, $\left| \left\langle g \right\rangle \right|=\left| g \right|$ 이다.
증명) ① $\Longleftarrow$ : $k=0$ 이면 분명하게 $g^0=1$ 이다.
$\Longrightarrow$ : $g^k=1\;(k\neq 0)$ 이라고 하자. 그러면 $g^{-k}=(g^k)^{-1}=1^{-1}=1$ 또한 성립하게 된다. 이것은 $g^n=1$ 이 되게 하는 $n\in\mathbb{N}$ 이 존재한다는 것이므로 $\left| g \right|$ 가 유한하다는 것을 뜻하여 우리의 가정에 모순이다.
② $$g^k=g^m\;\;\Longleftrightarrow \;\;
g^{k-m}=1 \;\;
\underset{\text{by ①}}\Longleftrightarrow \;\; k-m=0
\;\;\Longleftrightarrow \;\; k=m$$
이다. $\left| g \right| =\infty$ 이므로 여기서 $\infty\mid (k-m)$ 의 논리를 사용할 수는 없다.
③ ②에 의하여, 만일 $g^i=g^j$ 가 성립하면 $i=j$ 여야만 한다. 따라서 모든 서로 다른 $i\in\mathbb{Z}$ 에 대하여 $g^i$ 들 또한 서로 다른 값을 가진다. $_\blacksquare$
따름정리의 증명) $\left| g \right|=n$ 으로 유한한 경우, 정리($A.A$) 2.20)-③ 에 의하여 $\left| \left\langle g \right\rangle \right|$ 의 원소의 개수는 총 $n$ 개 존재한다. 따라서 $\left| \left\langle g \right\rangle \right|=\left| g \right|=n$ 으로 같다.
$\left| g \right|=\infty$ 인 경우, 위 정리($A.A$) 2.21)-③ 에 의하여 $\left| \left\langle g \right\rangle \right|$ 의 원소의 개수는 무한하고, 말하자면 $\aleph_0$ 인 셈이다. 따라서 $\left| \left\langle g \right\rangle \right|=\left| g \right|=\infty$ 이다. $_\blacksquare$
아래의 정리는 원소의 위수를 구하는 좋은 방법 중 하나입니다.
정리($A.A$) 2.22) 일반군에서 위수 계산법
군 $G$ 를 생각하고 $g\in G$ 에 대해 $\left| g \right|=n$ 이라 하자. 그러면 다음이 성립한다.
① $1\leq d\in\mathbb{N}$ 가 $d\mid n$ 이면, $\left| g^d \right|=\displaystyle\frac{n}{d}$ 가 성립한다.
② $k\in\mathbb{Z}$ 에 대하여 $\left| g^k \right|=\displaystyle \frac{n}{\gcd(n,k)}$ 가 성립한다.
증명) ① $(g^d)^{\frac{n}{d}}=g^n=1$ 인 것은 분명하다. 그러면 $\displaystyle\frac{n}{d}$ 라는 값이 $(g^d)$ 의 거듭제곱이 $1$ 이 되게 하는 정수 중 최솟값임을 보이면 충분하다.
편의상 $\left| \displaystyle \frac{n}{d} \right|:=k\in\mathbb{N}$ 이라 두고 $(g^d)^r=1\;(r\geq 1)$ 이라고 하자. 그러면 $g^{dr}=1$ 이므로 정리($A.A$) 2.20)-① 에 의하여 $n\mid (dr)$ 이어야 한다. 그러면 $dr=nq\;(1\leq q\in\mathbb{N})$ 으로 둘 수가 있다. 이로인해
$$dr=nq=(dk)q\;\;\Longrightarrow \;\; r=kq$$
의 관계가 성립하게 되고, $k,q\in\mathbb{N}$ 이기 때문에 $r=kq\geq k=\displaystyle\frac{n}{d}$ 가 성립한다. 따라서 $\displaystyle\frac{n}{d}$ 는 $r$ 값 중 최솟값으로, $\left| g^d \right|=\displaystyle\frac{n}{d}$ 가 성립한다.
② $m=\left| g^k \right|$ 라 하자. 그러면
$$\left( g^k \right)^{\displaystyle \frac{n}{\gcd(n,k)}}=\left( g^n \right)^{\displaystyle \frac{k}{\gcd(n,k)}} =1$$
이 되고, 여기서 $d:=\gcd(n,k)$ 라 하고 정리($A.A$) 2.20)-① 에 의해
$$m\mid\frac{n}{d}\;\;\;\;\;\cdots \;\;\;(1)$$
가 된다.
한편, 베주항등식을 이용하면 $d=\gcd(n,k)=xn+yk$ 가 성립하게 하는 $x,y\in\mathbb{Z}$ 가 존재한다. 이를 $(g^k)^m=1$ 에 적용하게 되면
$$g^{dm}=(g^d)^m=(g^{nx})^m\cdot (g^{yk})^m=(g^{nm})^x\cdot (g^{ny})^y=1$$
이 되며, 고로 $n\mid (dm)$ 을 얻는다. 그러면 $qn=dm$ 을 만족하는 $q\in\mathbb{Z}$ 가 존재한다는 것이고, 정리하면 $q\cdot \displaystyle\frac{n}{d}$ 에서 $\displaystyle\frac{n}{d}\mid m$ 이 성립한다. 이를 $(1)$ 과 결합하면 $m=\displaystyle\frac{n}{d}$ 를 얻는다. $_\blacksquare$
3. 순환군의 성질과 응용
1) 순환군의 기본 성질
정리($A.A$) 2.23) 순환군의 성질
① 모든 순환군은 아벨군이다. 물론 역은 성립하지 않는다.
② 모든 순환군의 부분군도 순환군이다.
증명) ① $C_n=\left\langle g \right\rangle=\left\{ 1,g,g^2,\cdots ,g^{n-1} \right\}
=\left\{ g^n\mid n\in\mathbb{N}\right\}$ 이라고 하고 임의의 $a,b\in C_n$ 을 생각하면, $C_n$ 은 군이고 군에서는 정리($A.A$) 2.10) 에 의하여 지수법칙이 성립하며 덧셈이라는 연산은 교환적이기 때문에
$$ab=g^kg^m=g^{k+m}=g^{m+k}=g^mg^k=ba$$
가 성립한다. 따라서 $C_n$ 의 임의의 두 원소에 대해 교환법칙이 성립하므로 $C_n$ 은 아벨군이다.
역은 반례를 제시함으로서 증명한다. $G:=\mathbb{Z}_2\times \mathbb{Z}_2$ 를 고려하자. 그러면 $\overline{0}\cdot \overline{0}= \overline{0}$, $\overline{0}\cdot \overline{1}=\overline{1}$, $\overline{1}\cdot \overline{0}=\overline{1}$, $\overline{1}\cdot \overline{1}=\overline{0}$ 이 성립한다. 따라서 임의의 $g,h\in G$ 에 대하여 $gh=hg$ 가 성립하는 것이다. 고로 $\mathbb{Z}_2\times \mathbb{Z}_2$ 는 아벨군이지만, 위수가 $4$ 인 원소는 존재하지 않으므로 순환군이 아니다. 예제 6) 에서 다루었던 $\mathbb{Z}_8^*$ 또한 아벨군이지만 순환군은 아니다.
② $G$ 가 순환군이고 $H\leqslant G$ 라 하자. $H=\{ 1\}$ 이면 자명히 $H$ 는 순환군이니 $H\neq \{ 1\}$ 인 경우에 대해 생각해보자.
$H\leqslant G$ 이므로, 적당한 $k\in\mathbb{Z}$ 에 대해 $g^k\in H$ 일 것이다.7 이때 $g^k\in H$ 인 $k$ 의 값 중 최소인 값을 $m$ 이라고 하자. 그러면 정리($A.A$) 2.17)-② 에 의하여 $\left\langle g^m \right\rangle \subseteq H$ 가 성립한다.
주어진 정리는 $H=\left\langle g^m \right\rangle$ 임을 증명하면 충분하므로 나머지 집합 관계를 보이고자 한다. 이를 위해서는 임의의 $g^k\in H$ 를 생각했을 때 $k=qm$ 의 형태가 되어야 함을 뜻한다.
나눗셈 알고리즘을 사용하여, 임의의 $m\leq k\in\mathbb{N}$ 에 대하여 $k=qm+r\;\;(0\leq r < m)$ 이라고 생각하자. 그러면
$$g^k=g^{mq+r}=(g^m)^q\cdot g^r$$
이고, 여기서 소거법칙을 써서 $g^r=g^k(g^m)^{-q}$ 가 된다. 그런데 $g^k, g^m\in H$ 가 성립하고 $H$ 는 군이므로 연산에 대해 닫혀있어서 $g^r\in H$ 가 된다. 이때, $0\leq r < m$ 인데 $m$ 의 최소성과 유일성에 의하여 $r\neq m$ 이다. 고로 $r=0$ 이고, 정리하면 $k=qm$ 이다. 따라서 임의의 $g^k\in H$ 는 $g^k\in \left\langle g^m \right\rangle$ 이 되므로, 여기서 $H\subseteq \left\langle g^m \right\rangle$ 를 얻는다. 종합하면 $H=\left\langle g^m \right\rangle$ 으로 순환군이다. $_\blacksquare$
2) 생성원
여기까지를 다루면 순환군과 위수의 기본적인 개념을 익힌 것입니다. 이제 약간 응용 단계로 넘어가겠습니다.
정리($A.A$) 2.24) 순환군의 생성원은 유일하지 않을 수 있다
순환군 $C_n=\left\langle g \right\rangle$ 을 생각하자. 물론 여기서 $\left| g \right|=n$ 이다. 그러면 $g^k\in G$ 역시 $G$ 의 생성원이 되는 것, 다시말해 $G=\left\langle g^k \right\rangle$ 일 필요충분조건은 $\gcd(k,n)=1$ 인 것이다.
증명) $\Longrightarrow$ : $g\in G=\left\langle g^k \right\rangle$ 라 가정하자. 그러면 이것은 순환군이니 $(g^k)^m=g$ 가 되게 하는 $m\in\mathbb{Z}$ 가 존재한다. 여기서 $1=g^{km-1}$ 이 되고 가정에 의해 $\left| g \right|=n$ 인 상황이다. 그러면 정리($A.A$) 2.20)-① 에 의하여 $n\mid {km-1} \;\;\Longrightarrow qn=km-1$ 이 되게 하는 $q\in\mathbb{Z}$ 또한 존재한다. 이것을 베주항등식의 형태로 생각하면, $qn+km=1=\gcd(n,k)$ 인 셈이다.
$\Longleftarrow$ : 똑같이 베주항등식의 논리로 만일 $\gcd(n,k)=1$ 이면 $xk+yn=1$ 을 만족하는 $x,y\in\mathbb{Z}$ 가 존재한다. 따라서
$$\begin{align*}
g=g^1&=g^{xk+yn}=g^{xk}\cdot g^{yn}=(g^k)^x\cdot 1
\\\\&=(g^k)^x
\end{align*}$$
가 성립한다. 그런데, $g\in \left\langle g^k \right\rangle$ 이고, 임의의 $p\in\mathbb{Z}$ 에 대해 $g^p\in \left\langle g^k \right\rangle$ 역시 성립한다. 순환군이기 때문이다. 따라서 $g^p=(g^k)^x$ 라고 생각하면 $g=(g^k)^x \in\left\langle g^k \right\rangle$ 이다. 따라서 $G=\left\langle g^k \right\rangle$ 이다. $_\blacksquare$
이 정리는 두 가지 의의가 있습니다. 첫번째는 어떤 순환군의 생성원을 찾을 때 최대공약수만 확인하면 충분하다는 것입니다. 아래 예제로 검토해 볼 것입니다. 둘째로는 적어두었듯이 순환군의 생성원은 유일하지 않을 수도 있다는 것입니다. 만일 $G=\left\langle g \right\rangle$ 와 같이 쓰면 생성원은 $g\in G$ 임을 뜻합니다. 그런데 우리는 정리($A.A$) 2.24) 에서 순환군의 생성원이 유일하지는 않을 수도 있음을 살펴보았습니다. 예컨대 $g\in G=\left\langle g\right\rangle$ 의 한 부분군으로 $\{1,g^2,g^4,g^6\}$ 이라는 순환군을 생각해봅시다. 여기서 $g^8=1$ 이라고 하겠습니다. 그러면 이 부분군은 $\left\langle g^2 \right\rangle$ 로 적을 수도 있지만 $\left\langle g^4 \right\rangle$ 라고 적는 것도 가능합니다.
예제 7) $C_4=\{ 1,a,a^2, a^3\}$ 의 생성원을 모두 찾아라.
$C_n$ 의 위수는 $4$ 이다. 따라서 정리($A.A$) 2.24) 에 의하여 $\gcd(n,k)=1$ 이 되게 하는 원소들의 지수 $k$ 를 찾는다. 그러면 $\gcd(1,4)=\gcd(3,4)=1$ 이므로 $C_4=\left\langle a \right\rangle=\left\langle a^3 \right\rangle$ 에 해당한다. $_\blacksquare$
3) 순환군의 기본 정리
정리($A.A$) 2.25) 순환군의 기본정리
$G=\left\langle g \right\rangle$ 를 위수가 $n$ 인 순환군이라고 하자.
① $H\leqslant G$ 이면, 어떤 $d=\left| H \right| \mid n$ 에 대하여 $H=\left\langle g^d \right\rangle$ 이다.8
② 만일 $k\mid n$ 이라고 하자. 그러면 $\left\langle g^{\frac{n}{k}} \right\rangle$ 는 위수가 $k$ 인 $G$ 의 유일한 순환군이다.
증명) ① $H\leqslant G$ 이면, 정리($A.A$) 2.23)-② 에 의하여 순환군의 부분군도 순환군이므로 어떤 $m\in\mathbb{Z}$ 에 대하여 $H=\left\langle g^m \right\rangle$ 이라고 할 수 있다. 이때 $d:=\gcd (m,n)$ 이라고 하자. 그러면 우리가 보여야 할 것은 $d\mid n$ 인 $d\in\mathbb{N}$ 에 대하여 $H=\left\langle g^d \right\rangle$ 인 것이다. $d\mid m$ 이므로 $m=dq\;(q\in\mathbb{Z})$ 이라고 하자. 그러면
$$g^m=g^{dq}=(g^d)^q \in \left\langle g^d \right\rangle\;\;\Longrightarrow \;\;
H\subseteq \left\langle g^d \right\rangle$$
한변, 베주항등식에 의하여 $x,y\in\mathbb{Z}$ 에 대해 $d=xm+yn$ 으로 나타낼 수 있다. 그러면
$$\begin{align*}
g^d&=g^{xm+yn}=(g^m)^x\cdot(g^n)^y
\\\\&=(g^m)^x\in \left\langle g^m \right\rangle =H\;\;
\Longrightarrow \;\; \left\langle g^d \right\rangle\subseteq H
\end{align*}$$
이 성립하므로, $H=\left\langle g^d \right\rangle$ 이다. 그럼 여기서 정리($A.A$) 2.22) 와 따름정리($A.A$) 2.21.1) 을 결합하면,
$$\left| H \right|=\left| \left\langle g^d \right\rangle \right|=\left| g^d \right|=\frac{n}{d}$$
가 된다. 따라서 $\left| H \right|=\displaystyle \frac{n}{d}\mid n$ 의 관계도 성립한다.
② $K$ 가 $\left| K \right|=k\mid n$ 를 만족하는 $K\leqslant G$ 라고 가정하자. ① 에 의하면 $K=\left\langle g^d \right\rangle$ 로 쓸 수 있고 이때 $d\mid n$ 이다. 그러면 정리($A.A$) 2.22) 와 따름정리($A.A$) 2.21.1) 를 결합하면
$$\left| K \right|=\left| \left\langle g^d \right\rangle \right|=\left| g^d \right|=\frac{n}{d}=k$$
의 결과를 얻는다. 그러므로 $K=\left\langle g^k\right\rangle=\left\langle g^{\frac{n}{d}} \right\rangle$ 이다. $_\blacksquare$
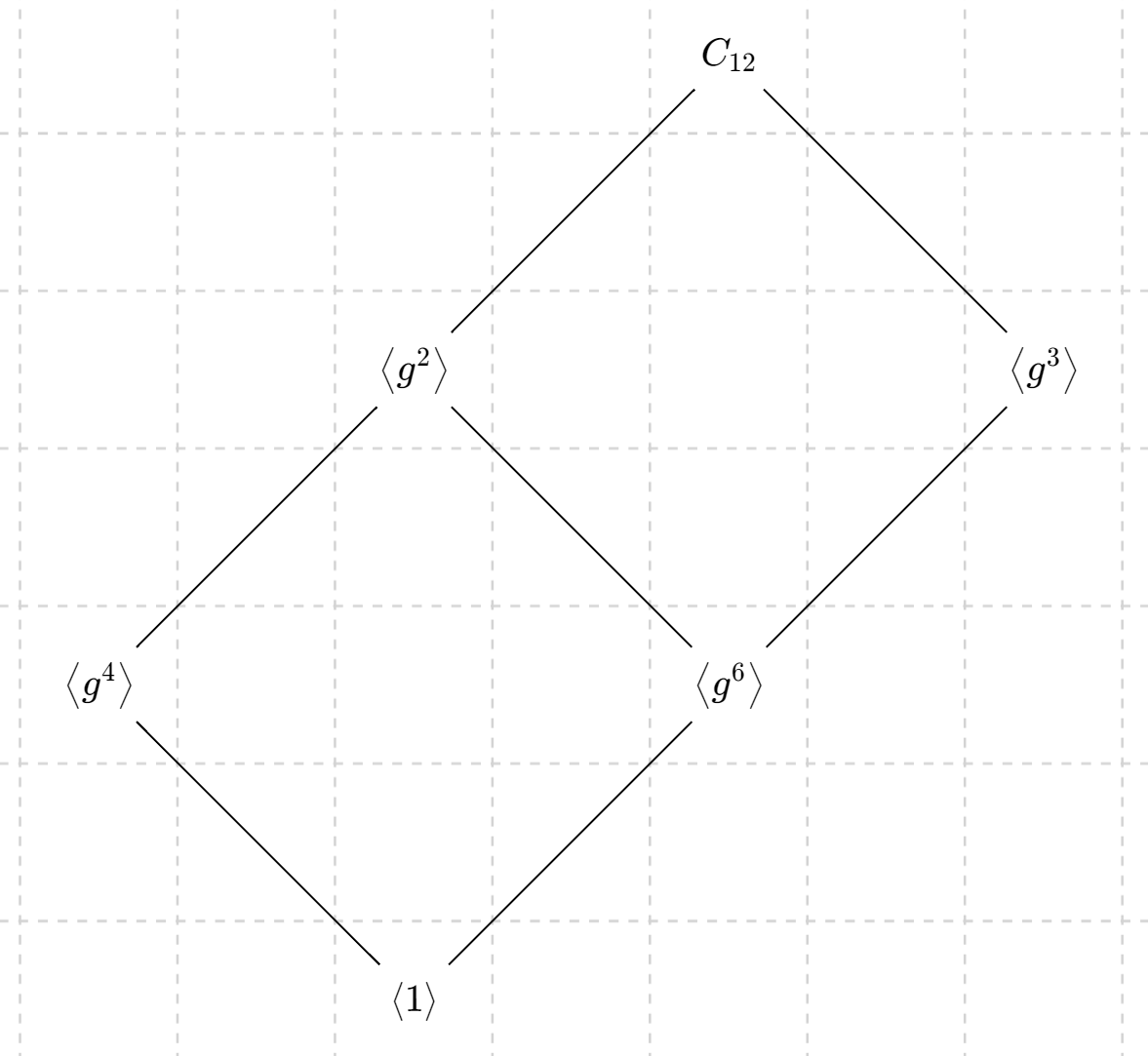
예제 8) $C_{12}$ 의 모든 부분군을 찾고, 격자 그림(Lattice diagram) 으로 위계 구조를 나타내 보아라.
Sol) $H\leqslant C_{12}$ 를 찾는 문제이다. 순환군의 기본정리에 의하면, 만일 $H$ 가 $C_{12}$ 의 부분군일 때 $H=\left\langle g^d \right\rangle$ 이고 $d\mid 12$ 가 되어야 한다. $12$ 의 약수는 $1,2,3,4,6,12$ 이다. 따라서 모든 부분군은
$$\left\langle g^2 \right\rangle, \left\langle g^3\right\rangle, \left\langle g^4 \right\rangle, \left\langle g^6\right\rangle, \left\langle g^{12} \right\rangle=\{1\},\;\;\text{and}\;\; C_{12}=\left\langle g^1 \right\rangle$$
이다. 여기서 $\left| \left\langle C_{12} \right\rangle \right|=12$ 이고 $C_{12}=\left\langle g \right\rangle$ 임에 유의하자. $_\blacksquare$
4. 순환군의 생성원 확장
다시 기본적인 순환군의 생성원 개념으로 돌아가 봅시다.
정리($A.A$) 2.26) 생성원의 집합
$G$ 가 군일 때 집합 $\emptyset\neq X\subseteq G$ 를 생각하자. 이때 $X$ 의 원소들의 가능한 모든 거듭제곱들의 곱들로 이루어진 집합
$$\left\langle X \right\rangle:=\left\{ x_1^{k_1}x_2^{k_2}\cdots x_m^{k_m} \mid x_i\in X\;,\;k_i\in \mathbb{Z}\;,\;m\geq 1\right\}$$ 을 고려하자. 그러면 다음이 성립한다.
① $X\subseteq \left\langle X \right\rangle \leqslant G$ 이며, 이는 $X$ 를 포함하는 $G$ 의 가장 작은 부분군이다. 그래서 $\left\langle X \right\rangle$ 를 '$X$ 에 의해 생성된 부분군'이라고 부르기도 한다.
② $X\subseteq H\leqslant G$ 이면, $\left\langle X \right\rangle \subseteq H$ 이다.
이때 어떤 $X\subseteq G$ 가 $G=\left\langle X \right\rangle$ 를 만족시키는 경우, $X$ 를 $G$ 아의 '생성원들의 집합(set of generators)'이라고 부른다. $X$ 가 유한집합이면, $G$ 는 '유한하게 생성된 군(finitely generated group)'이라고 부른다.
증명) ① 부분군 시험법을 사용하자. $X$ 가 공집합이 아니므로 어떤 $x\in X$ 를 선택할 수 있다. 그러면 $1=x^0\in \left\langle X \right\rangle$ 이다. 또한 $\left\langle X \right\rangle$ 는 연산에 대해 닫혀있는데 그 까닭은 지수법칙, 그리고 정수가 덧셈에 대해 닫혀있다는 사실로부터
$$\left( x_1^{k_1}x_2^{k_2}\cdots x_m^{k_m} \right)\left( x_1^{k_1'}x_2^{k_2'}\cdots x_m^{k_m'} \right)=\left( x_1^{k_1+k_1'}x_2^{k_2+k_2'}\cdots x_m^{k_m+k_m'} \right)\in \left\langle X \right\rangle$$
가 성립하기 때문이다. 마지막으로 $g=x_1^{k_1}x_2^{k_2}\cdots x_m^{k_m}\in \left\langle X \right\rangle$ 이라고 생각해보자. 어떤 정수 $z$ 에 대해 $-z$ 역시 정수이므로, $x_m^{-k_m}\cdots x_2^{-k_2} x_1^{-k_1} =g^{-1} \in \left\langle X \right\rangle$ 또한 성립한다. 그러므로 $\left\langle X \right\rangle \leqslant G$ 이며, 이것의 최소성을 보이는 일은 ② 를 마저 증명하면 충분하다.
② $a= x_1^{k_1}x_2^{k_2}\cdots x_m^{k_m} \in \left\langle X \right\rangle $ 라 할 때 $a\in H$ 를 보이면 충분하다. 가정에 의해 $X\subseteq H\leqslant G$ 이므로, 각각의 $x_i^j$ 들은 $G$ 의 원소이니 반드시 부분군 $H$ 에도 속해 있어야 한다. 그런데 $H$ 는 (부분)군이기 때문에, 연산에 대해 닫혀있다. 따라서 $a\in H$ 가 성립한다. $_\blacksquare$
예제 9) 차수가 3인 대칭군 $S_3=\left\{ 1,\sigma,\sigma^2,\tau, \tau\sigma, \tau\sigma^2 \right\}$ 를 생각하자. 여기서 $\left| \sigma \right|=3\;,\; \left| \tau \right|=2$ 이고 $\sigma\tau = \tau\sigma^2$ 이 성립한다. $S_3=\left\langle X \right\rangle$ 라 할 때, 집합 $X$ 를 찾아라.
Sol) $S_3$ 의 어떤 원소를 뽑아야, 이들 사이에 가능한 모든 조합의 곱으로 $S_3$ 의 모든 원소들을 만들어 낼 수 있는지를 보면 된다. $\sigma$ 를 $X$ 의 한 원소로 뽑아보자. 위수가 3이므로, 자기 자신을 여러번 거듭하여 곱하다 보면 $1,\sigma, \sigma^3$ 을 만들 수 있다. 또 $\tau$ 를 $X$ 의 한 원소로 뽑아보면, 자기 자신을 여러번 거듭 곱해서 $1,\tau$ 를 만들 수 있다.
이제 이 두 원소를 섞어서 곱해보자. 한 번씩 곱하면 $\sigma\tau\in S_3$ 를 만들 수 있다. $\sigma$ 를 두 번 곱하면 $\tau\sigma^2$ 도 만들 수 있다. 그렇기에 이 두 원소면 $S_3$ 의 모든 원소를 만들 수 있다. 따라서 $S_3=\left\langle \sigma, \tau \right\rangle$ 가 성립한다. $_\blacksquare$
[참고문헌]
Introduction to Abstract Algebra, 4e, W.Keith Nicholson
- 원래 대수학의 선수과목은 미적분학을 넘어서 집합론, 선형대수학, 정수론입니다. 셋 다 알아야 합니다. [본문으로]
- 따라서 아래 표기는 유한 순환군에 대한 것입니다. 순환군의 위수가 무한인 경우도 존재하는데, 그때는 아래와 똑같이 적지는 않습니다. [본문으로]
- 둘 중 무엇을 택하더라도 상관이 없다는 뜻. [본문으로]
- 이런 설명을 하는 이유는 다음과 같습니다. 생성원을 $1$ 로 택했을 때 모든 자연수는 $1$ 을 여러번 더함으로서 얻을 수 있으니 납득이 쉽습니다. 그런데 생성원을 $1$ 로 택했을 때 $-5$ 와 같은 음의 정수를 덧셈으로 만들어야 한다는 점을 떠올리면, $-5$ 는 $-1$ 을 5번 더한 것이니 생성원이 $1$ 이 아닐 것이라고 오해할 수 있습니다. 하지만 잘 생각해보면 군의 논리에 따라 만일 $g\in G$ 이면 $g^{-1}\in G$ 이어야 합니다. 즉 생성원 $1$ 또한 순환군의 원소이니 $-1$ 또한 군의 원소입니다. 그렇기에 $-5$ 를 해석할 때는 '생성원 $1$ 을 $-5$ 번 더한다'고 받아들이는 것은 적절하지 않으며, '$1$ 의 역원을 $5$ 번 더한다'고 사고해야 올바르다는 뜻입니다. 이를 꼭 전달하고자 구체적으로 부연 설명을 한 것입니다. [본문으로]
- 당연히 $a$ 자기 자신도 포함합니다. $a\mathcal{R}a$ [본문으로]
- 여기서 주의할 것은 $g$ 의 위수가 꼭 $m-k$ 라는 말은 아니라는 점이다. [본문으로]
- $G$ 가 순환군이기 때문에 $G$ 는 $g\in G$ 의 거듭제곱꼴들로 이루어져 있습니다. 그러면 $H$ 는 $G$ 의 부분군(그러니까 부분집합)이므로 $H$ 에 있는 항등원이 아닌 원소도 $g\in G$ 의 적당한 거듭제곱꼴로 이루어져 있을 것이라는 논리입니다. [본문으로]
- 이 결과는 사실 굳이 $G$ 가 순환군이라는 조건이 없어도 성립합니다. 이 사실을 말하는 것이 라그랑주 정리로, 뒤에서 곧 학습합니다. [본문으로]
'대수학(Abstract Algebra) > 군론' 카테고리의 다른 글
| 동형사상, 자기동형사상, 내부자기동형사상(Isomorphism, Automorphism, Inner automorphism) (0) | 2024.08.08 |
|---|---|
| 군의 준동형 사상(group homomorphism) (0) | 2024.07.31 |
| 여러가지 군(Various named group) (1) | 2024.06.21 |
| 부분군(Subgroup) (0) | 2024.02.23 |
| 대수학에서 군의 정의(Group in Algebra) (0) | 2024.02.23 |




댓글